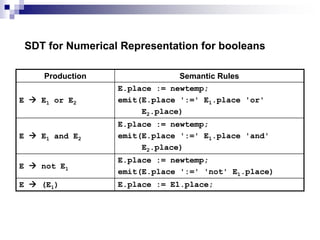
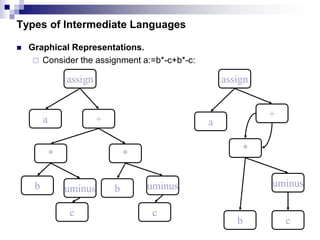
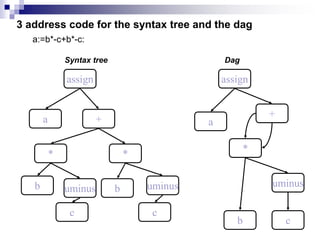
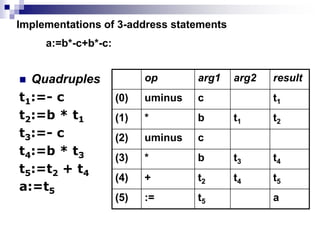
The document describes intermediate code generation during compilation. 1) An intermediate language is used to translate source programs into a form that is CPU independent yet close to machine language. This facilitates code optimization and retargeting of compilers. 2) Common intermediate languages include syntax trees, postfix notation, and three-address code using quadruples. Three-address code breaks down expressions into single assignment statements to simplify optimization. 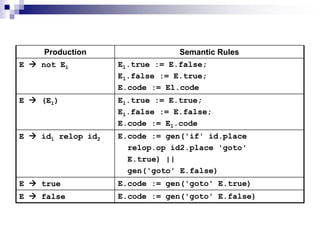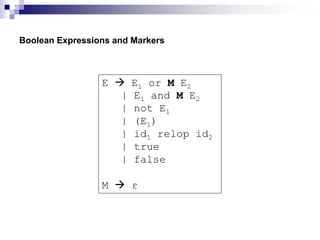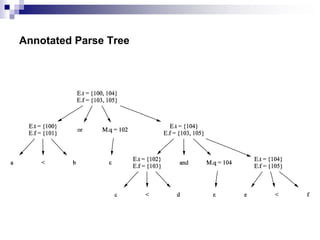3) Semantic rules for syntax-directed translation are described to generate three-address code for expressions, assignments, procedures, and other language constructs. Attributes track temporary variables and generated code.

1. Intermediate code generation
Shashwat Shriparv
dwivedishashwat@gmail.com
InfinitySoft

2. Intermediate Code Generation
 Translating source program into an
“intermediate language.”
 Simple
 CPU Independent,
 …yet, close in spirit to machine language.
 Benefits is
1. Retargeting is facilitated
2. Machine independent Code Optimization can be applied.

3. Intermediate Code Generation
 Intermediate codes are machine independent codes, but they are close to
machine instructions.
 The given program in a source language is converted to an equivalent program
in an intermediate language by the intermediate code generator.
 Intermediate language can be many different languages, and the designer of the
compiler decides this intermediate language.
 syntax trees can be used as an intermediate language.
 postfix notation can be used as an intermediate language.
 three-address code (Quadruples) can be used as an intermediate
language
 we will use quadruples to discuss intermediate code generation
 quadruples are close to machine instructions, but they are not actual
machine instructions.

4. Types of Intermediate Languages
 Graphical Representations.
 Consider the assignment a:=b*-c+b*-c:
assign
a +
* *
uminus uminusb
c c
b
assign
a
+
*
uminus
b c

5. Syntax Dir. Definition to produce syntax trees for
Assignment Statements.
PRODUCTION Semantic Rule
S  id := E { S.nptr = mknode (‘assign’,
mkleaf(id, id.entry), E.nptr) }
E  E1 + E2 {E.nptr = mknode(‘+’, E1.nptr,E2.nptr) }
E  E1 * E2 {E.nptr = mknode(‘*’, E1.nptr,E2.nptr) }
E  - E1 {E.nptr = mknode(‘uminus’, E1.nptr) }
E  ( E1 ) {E.nptr = E1.nptr }
E  id {E.nptr = mkleaf(id, id.entry) }

6. Three Address Code
 Statements of general form x:=y op z
 No built-up arithmetic expressions are allowed.
 As a result, x:=y + z * w
should be represented as
t1:=z * w
t2:=y + t1
x:=t2
 Observe that given the syntax-tree or the dag of the graphical
representation we can easily derive a three address code for assignments
as above.
 In fact three-address code is a linearization of the syntax tree.
 Three-address code is useful: related to machine-language/ simple/
optimizable.
x,y,z- names,constants or
compiler-generated temporaries
t1 , t2 – compiler generated temporary names

7. 3 address code for the syntax tree and the dag
a:=b*-c+b*-c:
assign
a +
* *
uminus uminusb
c c
b
assign
a
+
*
uminus
b c
Syntax tree Dag

8. 3-address codes are
t1:=- c
t2:=b * t1
t5:=t2 + t2
a:=t5
t1:=- c
t2:=b * t1
t3:=- c
t4:=b * t3
t5:=t2 + t4
a:=t5
Syntax tree Dag

9. Types of Three-Address Statements.
Assignment Statement: x:=y op z
Assignment Statement: x:=op z
Copy Statement: x:=z
Unconditional Jump: goto L
Conditional Jump: if x relop y goto L
Stack Operations: Push/pop
More Advanced
Procedure:
param x1
param x2
…
param xn
call p,n
Index Assignments:
x:=y[ i ]
x[ i ]:=y
Address and Pointer
Assignments:
x:=&y
x:=*y
*x:=y
Generated as part of
call of proc.
p(x1,x2,……,xn)

10. Syntax-Directed Translation into 3-address
code.

11. Syntax-Directed Translation for 3-address code for
assignment statements
 Use attributes
 E.place to hold the name of the “place” that will hold the value of
E
 Identifier will be assumed to already have the place attribute
defined.
 For example, the place attribute will be of the form t0, t1, t2, …
for identifiers and v0,v1,v2 etc. for the rest.
 E.code to hold the three address code statements that evaluate
E (this is the `translation’ attribute).
 Use function newtemp that returns a new temporary
variable that we can use.
 Use function gen to generate a single three address
statement given the necessary information (variable
names and operations).

12. Syntax-Dir. Definition for 3-address code
PRODUCTION Semantic Rule
S  id := E { S.code = E.code||gen(id.place ‘=’ E.place ) }
E  E1 + E2 {E.place = newtemp ;
E.code = E1.code || E2.code ||
|| gen(E.place‘:=’E1.place‘+’E2.place) }
E  E1 * E2 {E.place = newtemp ;
E.code = E1.code || E2.code ||
|| gen(E.place‘=’E1.place‘*’E2.place) }
E  - E1 {E.place = newtemp ;
E.code = E1.code ||
|| gen(E.place ‘=’ ‘uminus’ E1.place) }
E  ( E1 ) {E.place = E1.place ; E.code = E1.code}
E  id {E.place = id.entry ; E.code = ‘’ }
e.g. a := b * - (c+d)
‘||’: string concatenation

13. while statements
 E.g. while statements of the form “while E do S”
(interpreted as while the value of E is not 0 do S)
PRODUCTION
S  while E do S1
Semantic Rule
S.begin = newlabel;
S.after = newlabel ;
S.code = gen(S.begin ‘:’)
|| E.code
|| gen(‘if’ E.place ‘=’ ‘0’ ‘goto’ S.after)
|| S1.code
|| gen(‘goto’ S.begin)
|| gen(S.after ‘:’)
E.code
If E.place = 0 goto S.after
S1.code
Goto S.begin
S.begin:
S.after:
……………….
To mark the 1st stmt. In
code for E
stmt. following code S

14. Implementation of 3 address code
Quadruples
Triples
Indirect triples

15. Quadruples
 A quadruple is a record structure with four fields: op,
arg1, arg2, and result
 The op field contains an internal code for an operator
 Statements with unary operators do not use arg2
 Operators like param use neither arg2 nor result
 The target label for conditional and unconditional jumps are in
result
 The contents of fields arg1, arg2, and result are
typically pointers to symbol table entries

16. Implementations of 3-address statements
 Quadruples
t1:=- c
t2:=b * t1
t3:=- c
t4:=b * t3
t5:=t2 + t4
a:=t5
op arg1 arg2 result
(0) uminus c t1
(1) * b t1 t2
(2) uminus c
(3) * b t3 t4
(4) + t2 t4 t5
(5) := t5 a
a:=b*-c+b*-c:

17. Triples
 Triples refer to a temporary value by the position of
the statement that computes it
 Statements can be represented by a record with only three
fields: op, arg1, and arg2
 Avoids the need to enter temporary names into the symbol table
 Contents of arg1 and arg2:
 Pointer into symbol table (for programmer defined names)
 Pointer into triple structure (for temporaries)

18. Implementations of 3-address statements, II
 Triples
t1:=- c
t2:=b * t1
t3:=- c
t4:=b * t3
t5:=t2 + t4
a:=t5
op arg1 arg2
(0) uminus c
(1) * b (0)
(2) uminus c
(3) * b (2)
(4) + (1) (3)
(5) assign a (4)
a:=b*-c+b*-c:

19. Implementations of 3-address statements, III
 Indirect Triples
stmt op arg1 arg2
(14) uminus c
(15) * b (14)
(16) uminus c
(17) * b (16)
(18) + (15) (17)
(19) assign a (18)
stmt
(0) (14)
(1) (15)
(2) (16)
(3) (17)
(4) (18)
(5) (19)
t1:=- c
t2:=b * t1
t3:=- c
t4:=b * t3
t5:=t2 + t4
a:=t5
a:=b*-c+b*-c:

20. DECLARATIONS
 Declarations in a procedure
 Langs. like C , Pascal allows declarations in single procedure to
be processed as a group
 A global variable offset keeps track of the next available relative
addresses
 Before the Ist declaration is considered, the value of offset is set
to 0.
 When a new name is seen , name is entered in symbol table
with current value as offset , offset incre. by width of data object
denoted by name.
 Procedure enter(name,type,offset) creates symbol table entry
for name , gives it type type ,and rel.addr. offset in its data area
 Type , width – denotes no. of memory units taken by objects of
that type

21. SDT to generate ICode for Declarations
Using a global variable offset
PRODUCTION Semantic Rule
P  D { }
D  D ; D
D  id : T { enter (id.name, T.type, offset);
offset:=offset + T.width }
T  integer {T.type = integer ; T.width = 4; }
T  real {T.type = real ; T.width = 8}
T  array [ num ] of T1
{T.type=array(1..num.val,T1.type)
T.width = num.val * T1.width}
T  ^T1 {T.type = pointer(T1.type);T1.width = 4}

22. Nested Procedure Declarations
 For each procedure we should create a symbol table.
mktable(previous) – create a new symbol table where previous is
the parent symbol table of this new symbol table
enter(symtable,name,type,offset) – create a new entry for a variable
in the given symbol table.
enterproc(symtable,name,newsymbtable) – create a new entry for the
procedure in the symbol table of its parent.
addwidth(symtable,width) – puts the total width of all entries in the
symbol table into the header of that table.
 We will have two stacks:
 tblptr – to hold the pointers to the symbol tables
 offset – to hold the current offsets in the symbol tables in tblptr
stack.

23. SDT to generate ICode for Nested Procedures
( P  M D { addwidth(top(tblptr), top(offset)); pop(tblptr);
pop(offset) }
M   { t:=mktable(null); push(t, tblptr); push(0, offset)}
D  D1 ; D2 ...
D  proc id ; N D ; S { t:=top(tblpr); addwidth(t,top(offset));
pop(tblptr); pop(offset);
enterproc(top(tblptr), id.name, t)}
N   {t:=mktable(top(tblptr)); push(t,tblptr); push(0,offset);}
D  id : T {enter(top(tblptr), id.name, T.type, top(offset);
top(offset):=top(offset) + T.width
Example: proc func1; D; proc func2 D; S; S

24. SDT to generate ICode for assignment statements
 Use attributes
 E.place to hold the name of the “place” that will hold the value of
E
 Identifier will be assumed to already have the place attribute
defined.
 For example, the place attribute will be of the form t0, t1, t2, …
for identifiers and v0,v1,v2 etc. for the rest.
 E.code to hold the three address code statements that evaluate
E (this is the `translation’ attribute).
 Use function newtemp that returns a new temporary
variable that we can use.
 Use function gen to generate a single three address
statement given the necessary information (variable
names and operations).

25. Syntax-Dir. Definition for 3-address code
PRODUCTION Semantic Rule
S  id := E { S.code = E.code||gen(id.place ‘=’ E.place ) }
E  E1 + E2 {E.place = newtemp ;
E.code = E1.code || E2.code ||
|| gen(E.place‘:=’E1.place‘+’E2.place) }
E  E1 * E2 {E.place = newtemp ;
E.code = E1.code || E2.code ||
|| gen(E.place‘=’E1.place‘*’E2.place) }
E  - E1 {E.place = newtemp ;
E.code = E1.code ||
|| gen(E.place ‘=’ ‘uminus’ E1.place) }
E  ( E1 ) {E.place = E1.place ; E.code = E1.code}
E  id {E.place = id.entry ; E.code = ‘’ }
e.g. a := b * - (c+d)

26. Boolean Expressions
 Boolean expressions has 2 purpose
 To compute Boolean values
 as a conditional expression for statements
 Methods of translating boolean expression:
(2 methods to represent the value of Boolean expn)
 Numerical methods:
 True is represented as 1 and false is represented as 0
 Nonzero values are considered true and zero values are considered
false
 By Flow-of-control :
 Represent the value of a boolean by the position reached in a
program
 Often not necessary to evaluate entire expression

27. SDT for Numerical Representation for booleans
 Expressions evaluated left to right using 1 to denote
true and 0 to donate false
 Example: a or b and not c
t1 := not c
t2 := b and t1
t3 := a or t2
 Another example: a < b
100: if a < b goto 103
101: t : = 0
102: goto 104
103: t : = 1
104: …

28. Emit & nextstat
 emit fn.– places 3-address stmts into an o/p
file in the right format
 nextstat fn.– gives the index of the next 3 -
address stmt in o/p sequence
 E.place to hold the name of the “place” that
will hold the value of E

29. Production Semantic Rules
E  E1 or E2
E.place := newtemp;
emit(E.place ':=' E1.place 'or'
E2.place)
E  E1 and E2
E.place := newtemp;
emit(E.place ':=' E1.place 'and'
E2.place)
E  not E1
E.place := newtemp;
emit(E.place ':=' 'not' E1.place)
E  (E1) E.place := E1.place;
SDT for Numerical Representation for booleans

30. Production Semantic Rules
E  id1 relop id2
E.place := newtemp;
emit('if' id1.place relop.op
id2.place 'goto' nextstat+3);
emit(E.place ':=' '0');
emit('goto' nextstat+2);
emit(E.place ':=' '1');
E  true
E.place := newtemp;
emit(E.place ':=' '1')
E  false
E.place := newtemp;
emit(E.place ':=' '0')
SDT for Numerical Representation for booleans
nextstat fn.– gives the index of the next 3 - address stmt
in o/p sequence

31. Example: a<b or c<d and e<f
100: if a < b goto 103
101: t1 := 0
102: goto 104
103: t1 := 1
104: if c < d goto 107
105: t2 := 0
106: goto 108
107: t2 := 1
108: if e < f goto 111
109: t3 := 0
110: goto 112
111: t3 := 1
112: t4 := t2 and t3
113: t5 := t1 or t4

32. Flow of control Stmts
 S →if E then S1 |
if E then S1 else S2|while E do S1
 Here E is the boolean expn. to be translated
 We assume that 3-address code can be labeled
 newlabel returns a symbolic label each time its called.
 E is associated with 2 labels
1. E.true – label which controls flow if E is true
2. E.false – label which controls flow if E is false
 S.next – is a label that is attached to the first 3 address
instruction to be executed after the code for S

33. 1. Code for if - then
E.code
S1.code
to E.true
to E.false
………..
S →If E then S1
Semantic rules
E.true := newlabel;
E.false := S.next;
S1.next := S.next;
S.code := E.code ||
gen(E.true ':') ||
S1.code
E.true:
E.false:

34. 2.Code for if-then-else
S  if E then S1 else S2
E.code
S1.code
to E.true
to E.false
Semantic rules
goto S.next
S2.code
E.true:
E.false:
………..S.next
E.true := newlabel;
E.false := newlabel;
S1.next := S.next;
S2.next := S.next;
S.code := E.code ||
gen(E.true ':') ||
S1.code ||
gen(‘ goto‘ S.next) ||
gen ( E.false ‘:’ ) ||
S2.code

35. 3. Code for while-do
S  while E do S1
E.code
S1.code
to E.true
to E.false
Semantic rules
S.begin := newlabel;
E.true := newlabel;
E.false := S.next;
S1.next := S.begin;
S.code := gen(S.begin ':') ||
E.code ||
gen(E.true ':') ||
S1.code ||
gen('goto' S.begin)
goto S.begin
E.true:
E.false: ………..
S.begin

36. Jumping code/Short Circuit code for boolean
expression
 Boolean Expressions are translated in a sequence of
conditional and unconditional jumps to either E.true or
E.false.
 a < b. The code is of the form:
if a < b then goto E.true
goto E.false
 E1 or E2. If E1 is true then E is true, so E1.true = E.true.
Otherwise, E2 must be evaluated, so E1.false is set to
the label of the first statement in the code for E2.
 E1 and E2. Analogous considerations apply.
 not E1. We just interchange the true and false with that
for E.

37. Production Semantic Rules
E  E1 or E2
E1.true := E.true;
E1.false := newlabel;
E2.true := E.true;
E2.false := E.false;
E.code := E1.code ||
gen(E1.false ':') || E2.code
E  E1 and E2
E1.true := newlabel;
E1.false := E.false;
E2.true := E.true;
E2.false := E.false;
E.code := E1.code ||
gen(E1.true ':') || E2.code
Control flow translation of boolean expression
We will now see the code produced for the boolean expression E

38. Production Semantic Rules
E  not E1 E1.true := E.false;
E1.false := E.true;
E.code := E1.code
E  (E1) E1.true := E.true;
E1.false := E.false;
E.code := E1.code
E  id1 relop id2 E.code := gen('if' id.place
relop.op id2.place 'goto'
E.true) ||
gen('goto' E.false)
E  true E.code := gen('goto' E.true)
E  false E.code := gen('goto' E.false)

39. Example
while a < b do
if c < d then
x := y + z
else
x := y - z

40. Example
Lbegin: if a < b goto L1
goto Lnext
L1: if c < d goto L2
goto L3
L2: t1 := y + z
x := t1
goto Lbegin
L3: t2 := y - z
x := t2
goto Lbegin
Lnext:
while a < b do
if c < d then
x := y + z
else
x := y - z

41. Case Statements
 Switch <expression>
begin
case value : statement
case value : statement
……..
case value : statement
default : statement
end

42. Translation of a case stmt
code to evaluate E into t
goto test
L1: code for S1
goto next
…
Ln-1: code for Sn-1
goto next
Ln: code for Sn
goto next
test: if t = V1 goto L1
…
if t = Vn-1 goto Ln-1
goto Ln
next:

43. Backpatching
 Easiest way to implement Syntax directed defn. is to
use 2 passes
 First, construct syntax tree
 Walk through syntax tree in depth-first order,
computing translations
 May not know the labels to which control must flow
at the time a jump is generated
 Affect boolean expressions and flow control statements
 Leave targets of jumps temporarily unspecified
 Add each such statement to a list of goto statements whose
labels will be filled in later
 This filling in of labels is called back patching
How backpatching is implemented in 1 pass….?

44. Lists of Labels
 Imagine that we are generating quadruples into a
quadruple array.
 Labels are indices into this array
 To manipulate this list of labels we use 3 fns.
 makelist(i)
 Creates a new list containing only i, and index into the array of
quadruples
 Returns a pointer to the new list
 merge(p1, p2)
 Concatenates two lists of labels
 Returns a pointer to the new list
 backpatch(p, i) – inserts i as target label for each
statement on the list pointed to by p

45. Boolean Expressions and Markers
E  E1 or M E2
| E1 and M E2
| not E1
| (E1)
| id1 relop id2
| true
| false
M  ε

46. The New Marker , M
 Translation scheme suitable for producing
quadruples during bottom-up pass
 The new marker has an associated semantic action which
Picks up, at appropriate times, the index of the next quadruple
to be generated
 M.quad := nextquad
 Nonterminal E will have two new synthesized
attributes:
 E.truelist contains a list of statements that jump when
expression is true
 E.falselist contains a list of statements that jump when
expression is false

47. Example: E  E1 and M E2
 If E1 is false:
 Then E is also false
 So statements on E1.falselist become part of
E.falselist
 If E1 is true:
 Still need to test E2
 Target for statements on E1.truelist must be the
beginning of code generated for E2
 Target is obtained using the marker M

48. New Syntax-Directed Definition (1)
Production Semantic Rules
E  E1 or M E2
backpatch(E1.falselist, M.quad);
E.truelist := merge(E1.truelist,
E2.truelist);
E.falselist := E2.falstlist
E  E1 and M E2
backpatch(E1.truelist, M.quad);
E.truelist := E2.truelist;
E.falselist := merge(E1.falselist,
E2.falselist)
E  not E1
E.truelist := E1.falselist;
E.falselist := E1.truelist
E  (E1)
E.truelist := E1.truelist;
E.falselist := E1.falselist

49. New Syntax-Directed Definition (2)
Production Semantic Rules
E  id1 relop id2
E.truelist := makelist(nextquad);
E.falselist := makelist(nextquad+1);
emit('if' id1.place relop.op
id2.place 'goto _');
emit('goto _')
E  true
E.truelist := makelist(nextquad);
emit('goto _')
E  false
E.falselist := makelist(nextquad);
emit('goto _')
M  ε M.quad := nextquad

50. Example Revisited (1)
 Reconsider: a<b or c<d and e<f
 First, a<b will be reduced, generating:
100: if a < b goto _
101: goto _
 Next, the marker M in E  E1 or M E2 will be
reduced, and M.quad will be set to 102
 Next, c<d will be reduced, generating:
102: if c < d goto _
103: goto _

51. Example Revisited (2)
 Next, the marker M in E  E1 and M E2 will be
reduced, and M.quad will be set to 104
 Next, e<f will be reduced, generating:
104: if e < f goto _
105: goto _
 Next, we reduce by E  E1 and M E2
 Semantic action calls backpatch({102}, 104)
 E1.truelist contains only 102
 Line 102 now reads: if c <d goto 104

52. Example Revisited (3)
 Next, we reduce by E  E1 or M E2
 Semantic action calls backpatch({101}, 102)
 E1.falselist contains only 101
 Line 101 now reads: goto 102
 Statements generated so far:
100: if a < b goto _
101: goto 102
102: if c < d goto 104
103: goto _
104: if e < f goto _
105: goto _
 Remaining goto instructions will have their addresses filled in
later

53. Annotated Parse Tree

54. Procedure Calls
 Grammar
S -> call id ( Elist )
Elist -> Elist , E
Elist -> E
 Semantic Actions
1. S -> call id (Elist) for each item p in queue do
{ gen(‘param’ p)
gen(‘call’ id.place)
}

55. 2. Elist -> Elist , E {append E.place to the end of queue}
3. Elist -> E { initialize queue to contain only E.place}
e.g.
P (x1,x2,x3,…………….xn)
param x1
param x2
………….
………….
param xn
call P

56. Shashwat Shriparv
dwivedishashwat@gmail.com
InfinitySoft