The document consists of a series of mathematical questions categorized into sections, detailing various concepts in mathematics such as matrix operations, vector spaces, convergence of series, differential equations, and algebraic structures. Each question presents multiple-choice answers, testing knowledge on advanced mathematics topics. It serves as an examination or assessment tool for evaluating mathematical understanding, particularly at a graduate level.






![JAM 2022 MATHEMATICS - MA
MA 13/42
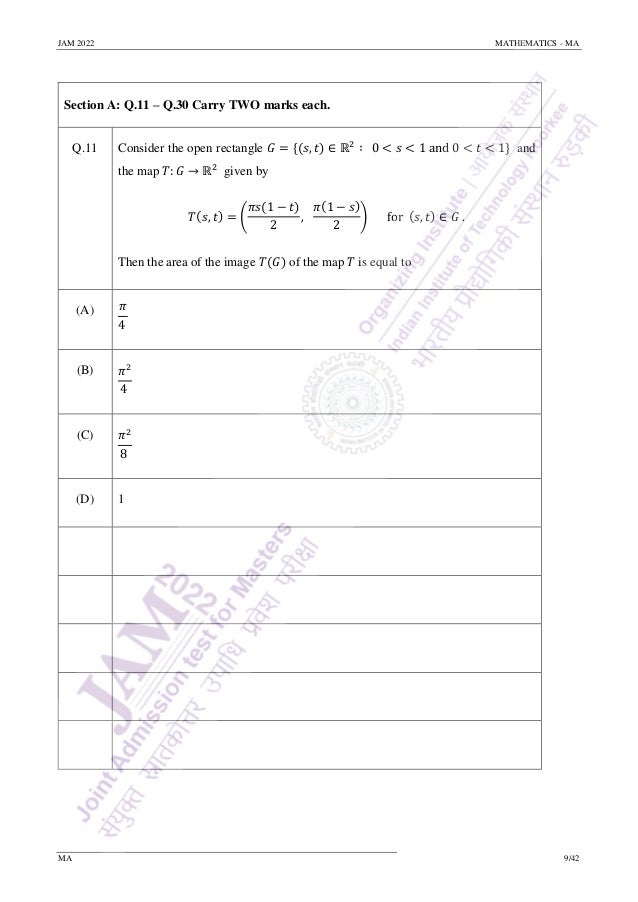
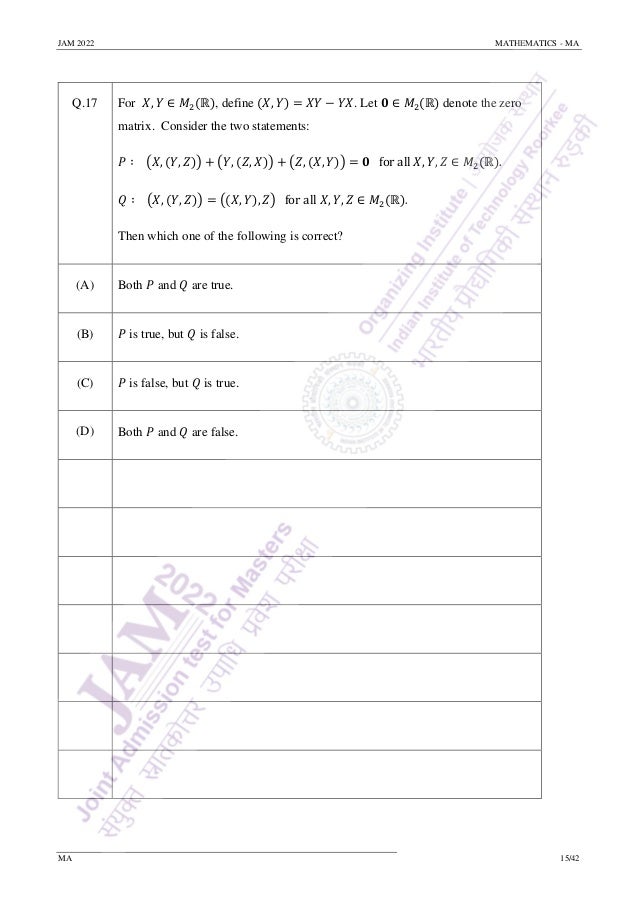
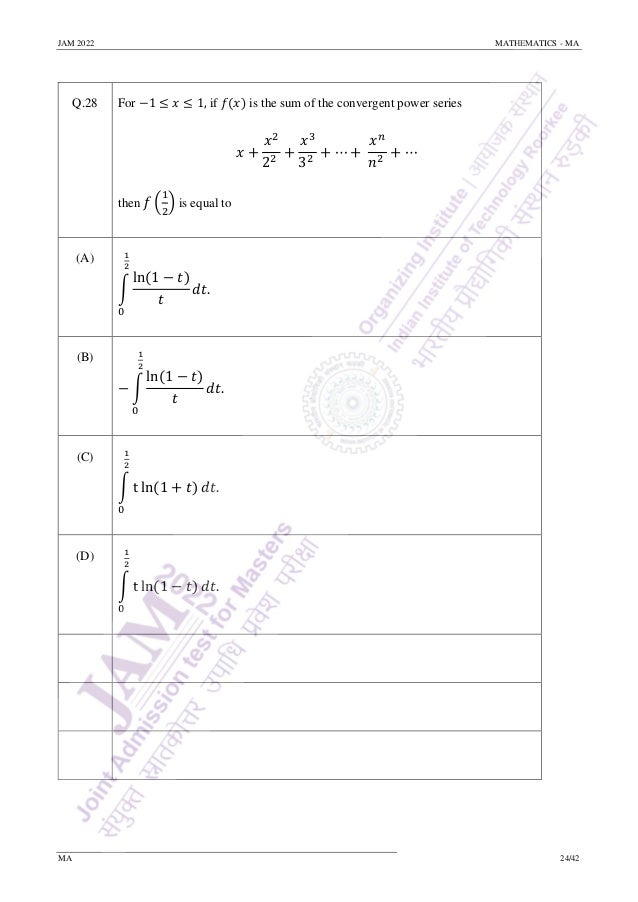
Q.15 For 𝑡 ∈ ℝ, let [𝑡] denote the greatest integer less than or equal to 𝑡. Define
functions ℎ: ℝ2
→ ℝ and 𝑔: ℝ → ℝ by
ℎ(𝑥, 𝑦) = {
−1
𝑥2−𝑦
if 𝑥2
≠ 𝑦,
0 if 𝑥2
= 𝑦
and 𝑔(𝑥) = {
sin 𝑥
𝑥
if 𝑥 ≠ 0,
0 if 𝑥 = 0.
Then which one of the following is FALSE?
(A)
lim
(𝑥,𝑦)→(√2,𝜋)
cos (
𝑥2
𝑦
𝑥2 + 1
) =
−1
2
.
(B) lim
(𝑥,𝑦)→(√2,2)
𝑒ℎ(𝑥,𝑦)
= 0.
(C) lim
(𝑥,𝑦)→(𝑒,𝑒)
ln(𝑥𝑦−[𝑦]
) = 𝑒 − 2.
(D) lim
(𝑥,𝑦)→(0,0)
𝑒2𝑦
𝑔(𝑥) = 1.](https://image.slidesharecdn.com/qpma-jam2022-220223132430/95/IIT-JAM-Math-2022-Question-Paper-Sourav-Sir-s-Classes-13-638.jpg)
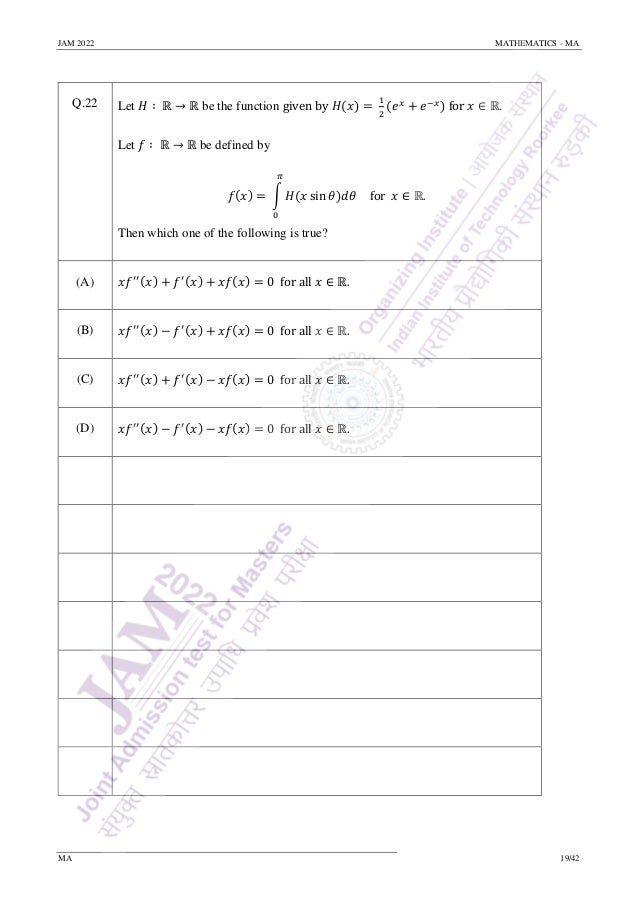

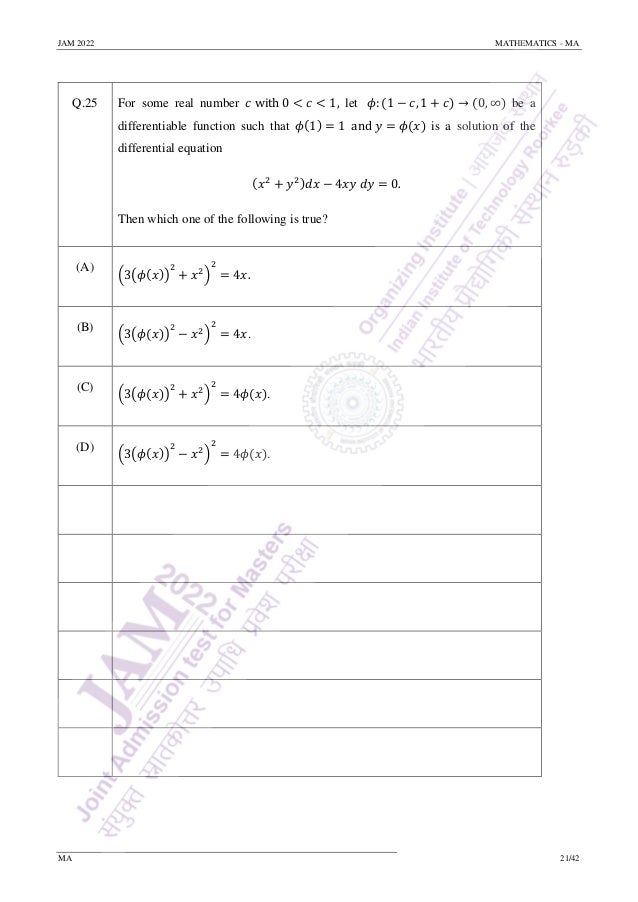
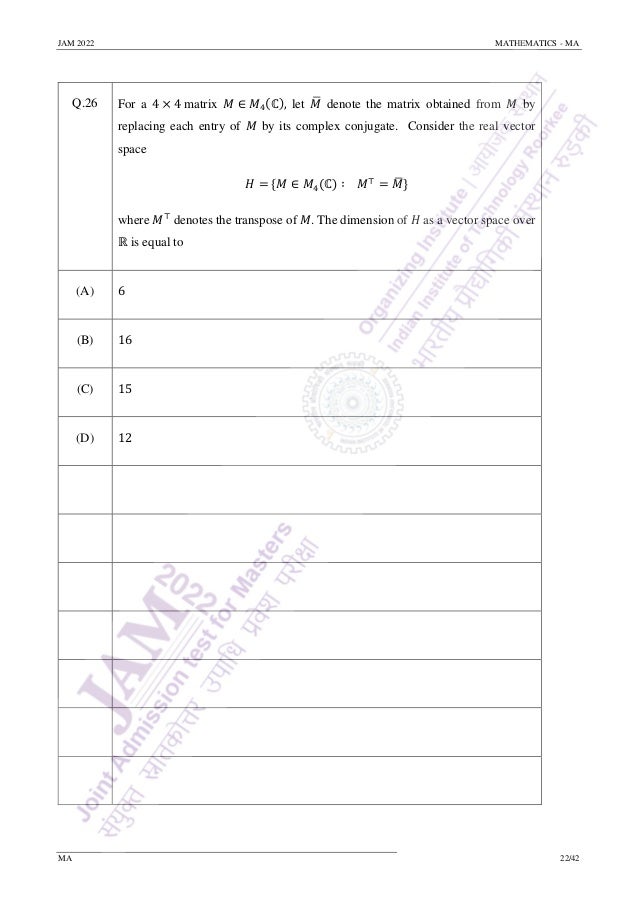
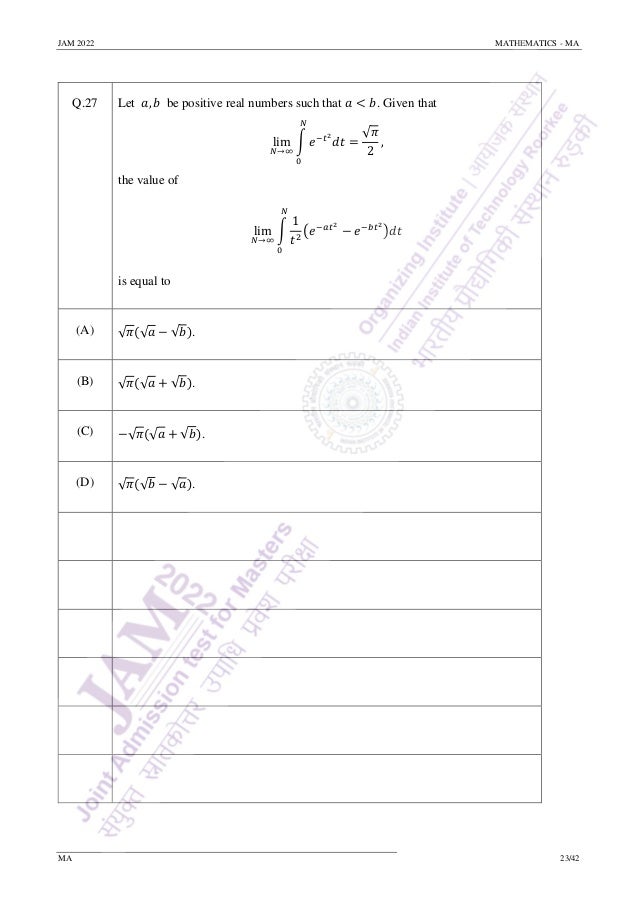


![JAM 2022 MATHEMATICS - MA
MA 27/42
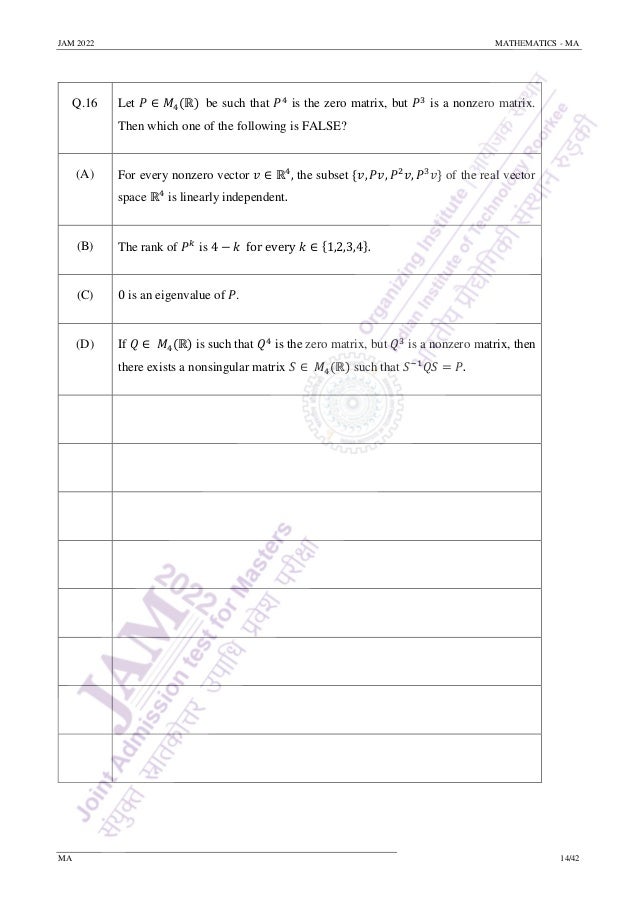
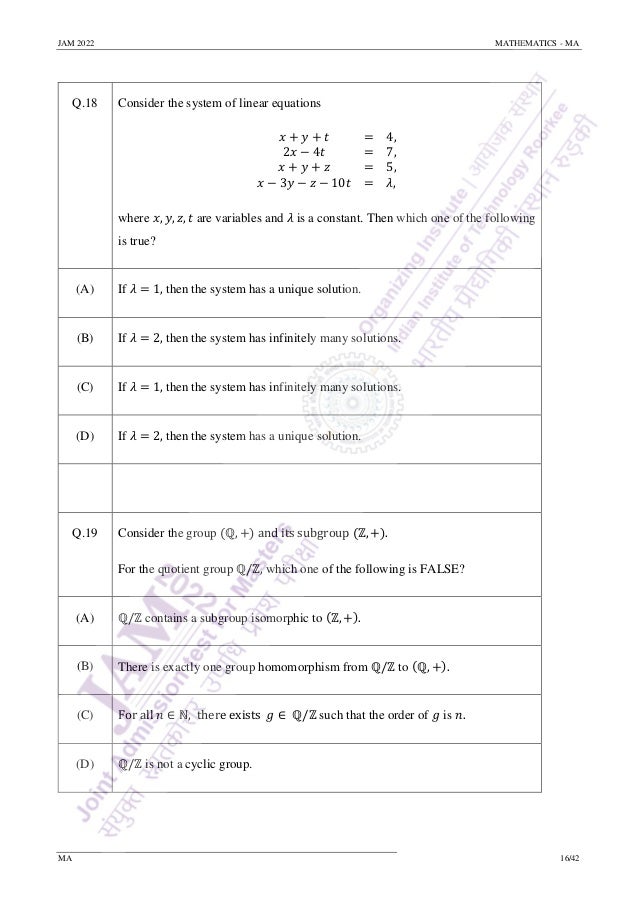
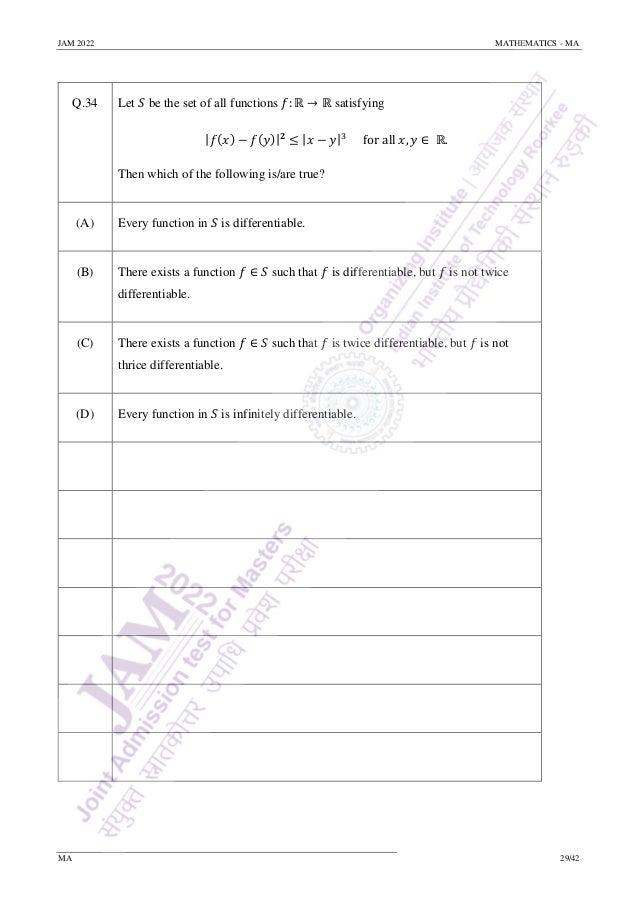
Q.32 Let 𝑆 be the set of all continuous functions 𝑓: [−1,1] → ℝ satisfying the following
three conditions:
(i) 𝑓 is infinitely differentiable on the open interval (−1,1),
(ii) the Taylor series
𝑓(0) + 𝑓′(0)𝑥 +
𝑓′′(0)
2!
𝑥2
+ ⋯
of 𝑓 at 0 converges to 𝑓(𝑥) for each 𝑥 ∈ (−1,1),
(iii) 𝑓 (
1
𝑛
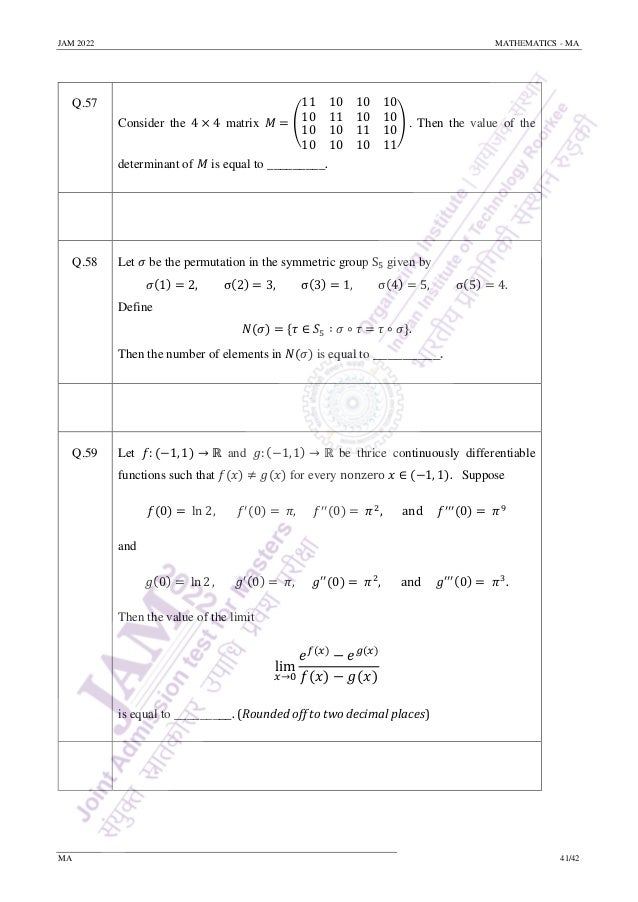
) = 0 for all 𝑛 ∈ ℕ.
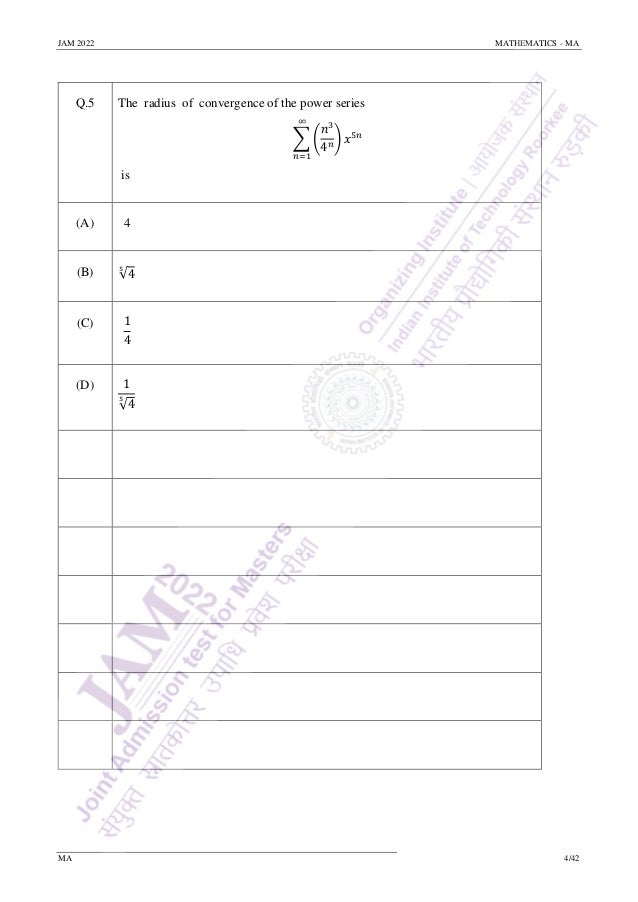
Then which of the following is/are true?
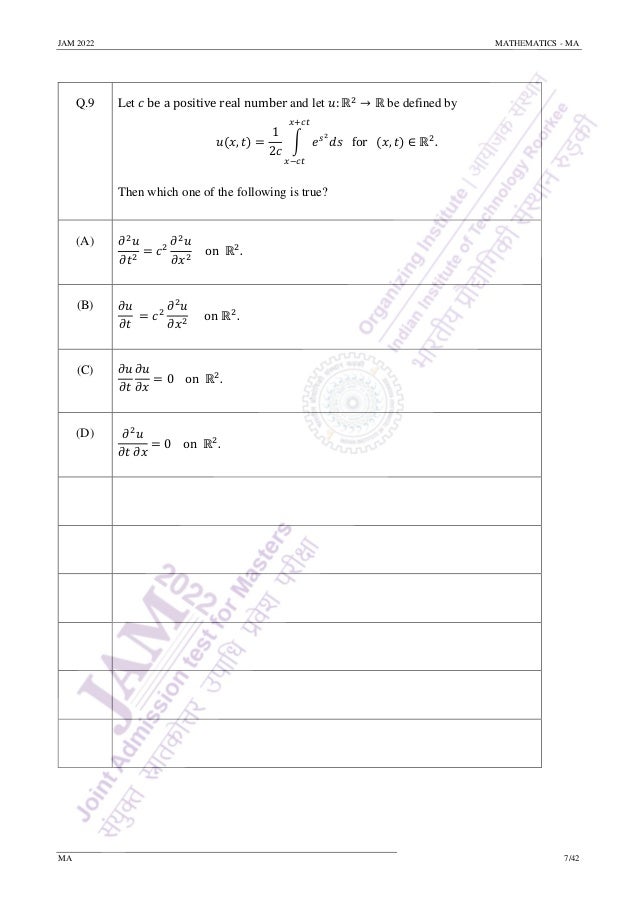
(A) 𝑓(0) = 0 for every 𝑓 ∈ 𝑆.
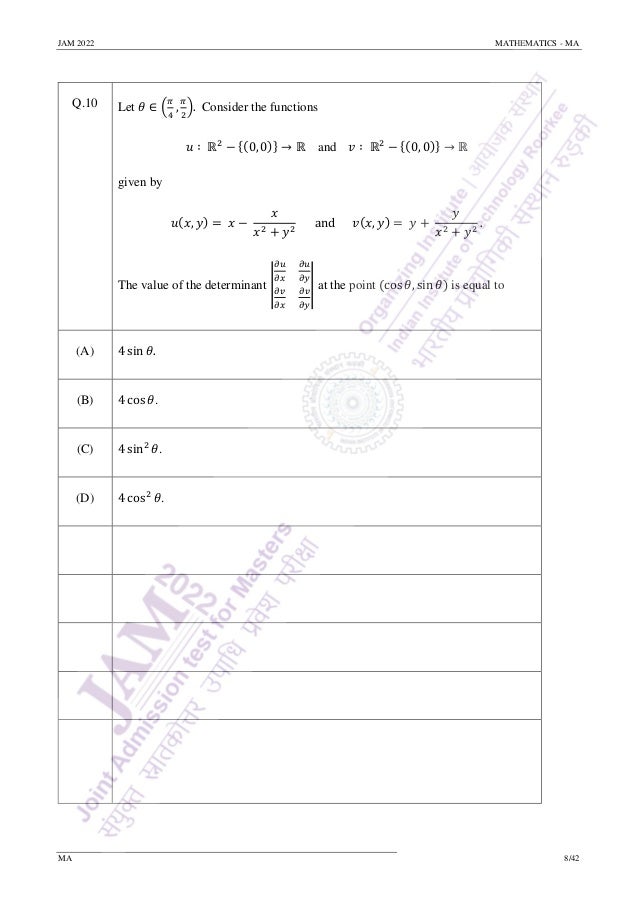
(B) 𝑓′ (
1
2
) = 0 for every 𝑓 ∈ 𝑆.
(C) There exists 𝑓 ∈ 𝑆 such that 𝑓′ (
1
2
) ≠ 0.
(D) There exists 𝑓 ∈ 𝑆 such that 𝑓(𝑥) ≠ 0 for some 𝑥 ∈ [−1,1].](https://image.slidesharecdn.com/qpma-jam2022-220223132430/95/IIT-JAM-Math-2022-Question-Paper-Sourav-Sir-s-Classes-27-638.jpg)
![JAM 2022 MATHEMATICS - MA
MA 28/42
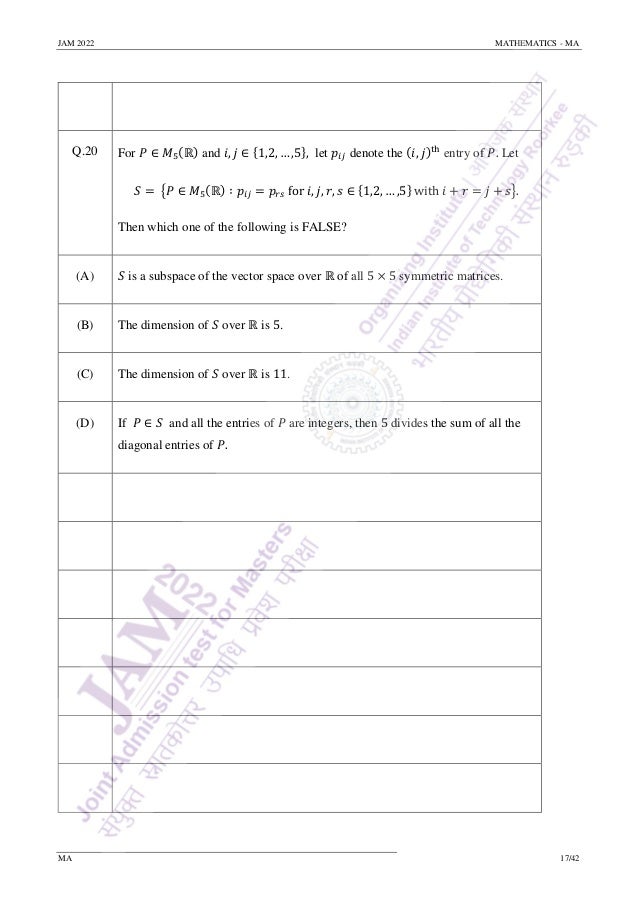
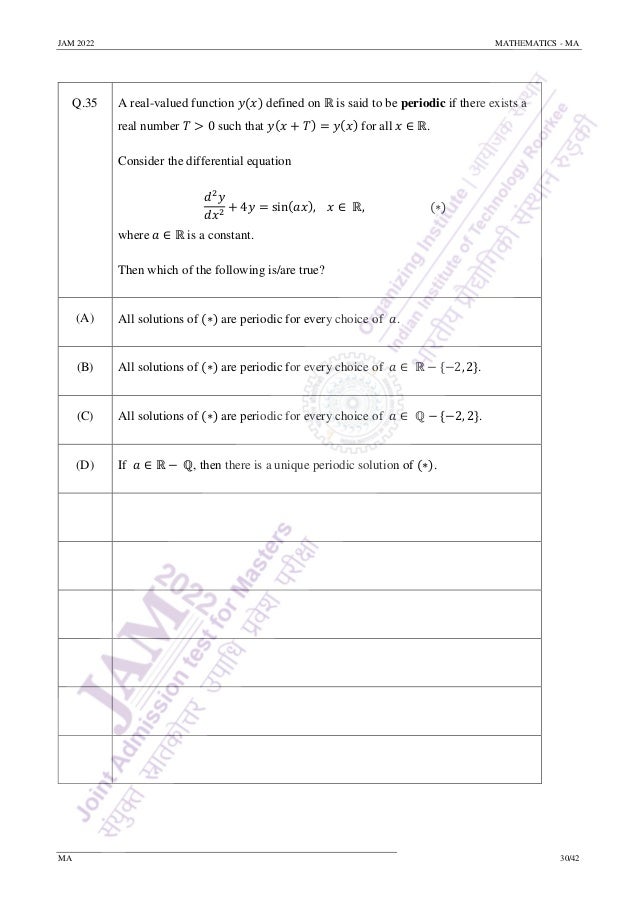
Q.33 Define 𝑓: [0,1] → [0,1] by
𝑓(𝑥) =
{
1 if 𝑥 = 0,
1
𝑛
if 𝑥 =
𝑚
𝑛
for some 𝑚, 𝑛 ∈ ℕ with 𝑚 ≤ 𝑛 and gcd(𝑚, 𝑛) = 1,
0 if 𝑥 ∈ [0,1] is irrational.
and define 𝑔: [0,1] → [0,1] by
𝑔(𝑥) = {
0 if 𝑥 = 0,
1 if 𝑥 ∈ (0,1].
Then which of the following is/are true?
(A) 𝑓 is Riemann integrable on [0,1].
(B) 𝑔 is Riemann integrable on [0,1].
(C) The composite function 𝑓 ∘ 𝑔 is Riemann integrable on [0,1].
(D) The composite function 𝑔 ∘ 𝑓 is Riemann integrable on [0,1].](https://image.slidesharecdn.com/qpma-jam2022-220223132430/95/IIT-JAM-Math-2022-Question-Paper-Sourav-Sir-s-Classes-28-638.jpg)





![JAM 2022 MATHEMATICS - MA
MA 38/42
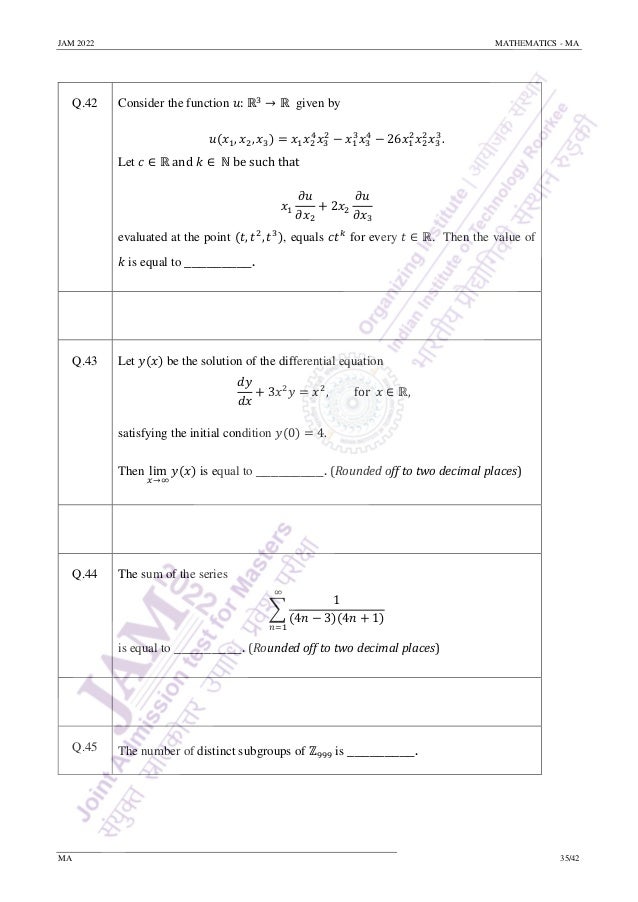
Section C: Q.51 – Q.60 Carry TWO marks each.
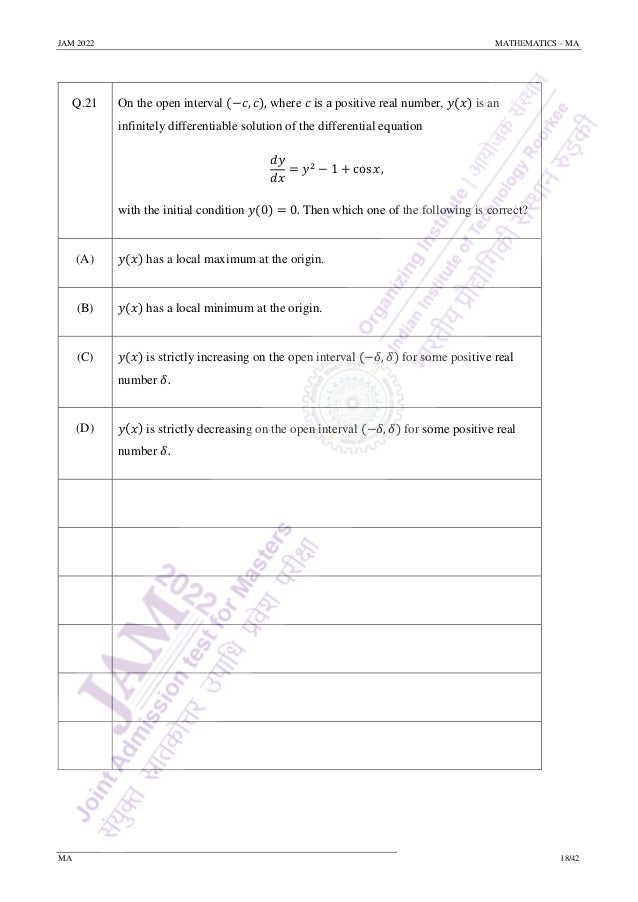
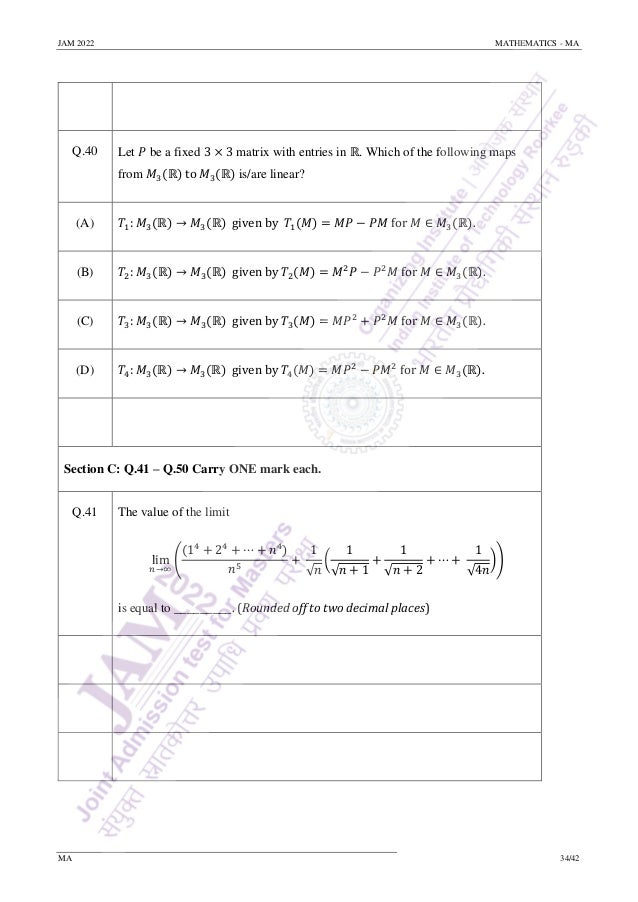
Q.51 For 𝑡 ∈ ℝ, let [𝑡] denote the greatest integer less than or equal to 𝑡.
Let 𝐷 = {(𝑥, 𝑦) ∈ ℝ2
∶ 𝑥2
+ 𝑦2
< 4}. Let 𝑓: 𝐷 → ℝ and 𝑔: 𝐷 → ℝ be defined
by 𝑓(0, 0) = 𝑔(0, 0) = 0 and
𝑓(𝑥, 𝑦) = [𝑥2
+ 𝑦2]
𝑥2
𝑦2
𝑥4 + 𝑦4
, 𝑔(𝑥, 𝑦) = [𝑦2]
𝑥𝑦
𝑥2 + 𝑦2
for (𝑥, 𝑦) ≠ (0, 0). Let 𝐸 be the set of points of 𝐷 at which both 𝑓 and 𝑔 are
discontinuous. The number of elements in the set 𝐸 is _________.
Q.52 If 𝐺 is the region in ℝ2
given by
𝐺 = {(𝑥, 𝑦) ∈ ℝ2
∶ 𝑥2
+ 𝑦2
< 1,
𝑥
√3
< 𝑦 < √3𝑥, 𝑥 > 0, 𝑦 > 0}
then the value of
200
𝜋
∬𝑥2
𝑑𝑥 𝑑𝑦
𝐺
is equal to _________. (Rounded off to two decimal places)](https://image.slidesharecdn.com/qpma-jam2022-220223132430/95/IIT-JAM-Math-2022-Question-Paper-Sourav-Sir-s-Classes-38-638.jpg)
![JAM 2022 MATHEMATICS - MA
MA 39/42
Q.53
Let 𝐴 = (
1 1
0 1
−1 1
) and let 𝐴⊤
denote the transpose of 𝐴. Let 𝑢 = (
𝑢1
𝑢2
) and
𝑣 = (
𝑣1
𝑣2
𝑣3
) be column vectors with entries in ℝ such that 𝑢1
2
+ 𝑢2
2
= 1 and
𝑣1
2
+ 𝑣2
2
+ 𝑣3
2
= 1. Suppose
𝐴𝑢 = √2 𝑣 and 𝐴⊤
𝑣 = √2 𝑢.
Then |𝑢1 + 2 √2 𝑣1| is equal to _________. (Rounded off to two decimal places)
Q.54 Let 𝑓: [0, 𝜋] → ℝ be the function defined by
𝑓(𝑥) = {
(𝑥 − 𝜋)𝑒sin 𝑥
if 0 ≤ 𝑥 ≤
𝜋
2
,
𝑥𝑒sin 𝑥
+
4
𝜋
if
𝜋
2
< 𝑥 ≤ 𝜋.
Then the value of
∫ 𝑓(𝑥)𝑑𝑥
𝜋
0
is equal to _________. (Rounded off to two decimal places)](https://image.slidesharecdn.com/qpma-jam2022-220223132430/95/IIT-JAM-Math-2022-Question-Paper-Sourav-Sir-s-Classes-39-638.jpg)