Download to read offline
![Artificial Over-Constrained Problem
Random Domain:
5 values on [1..15]
oj
every values 1..15
should appear exactly
once
on each row
oi
violation = sum
of excess &
shortage of each
value
every values 1..15 should
appear exactly once
on each column](https://image.slidesharecdn.com/ictai13-volns-131122230409-phpapp02/85/IACTAI13-Variable-Objective-Large-Neighborhood-Search-A-practical-approach-to-solve-over-constrained-problems-Pierre-Schaus-29-320.jpg)
Uploaded byPierre Schaus
IACTAI13 Variable Objective Large Neighborhood Search: A practical approach to solve over-constrained problems (Pierre Schaus)
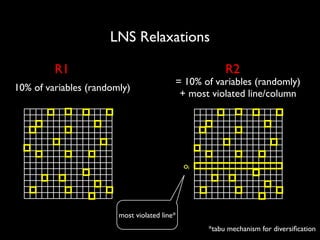
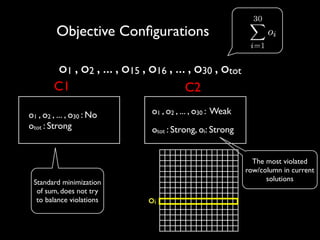
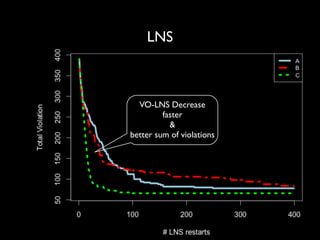
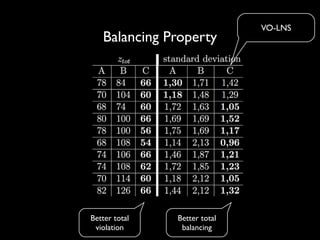
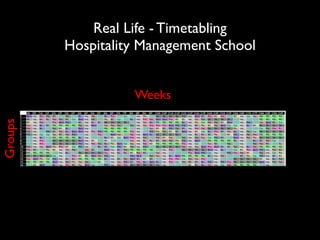
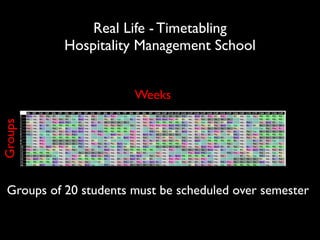
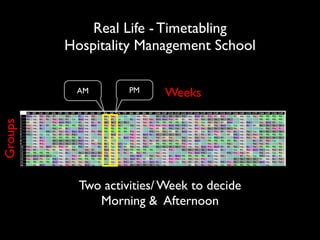
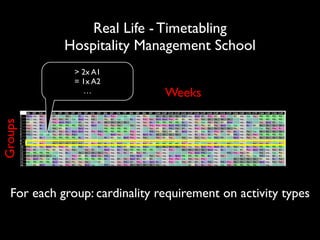
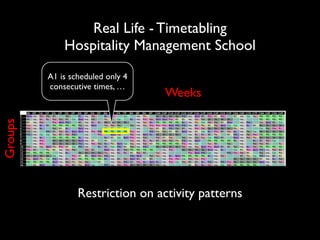
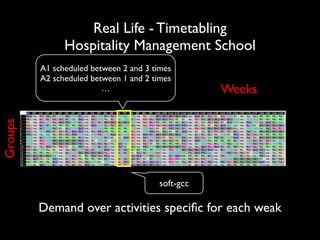
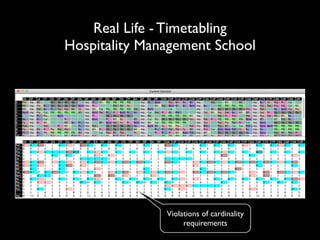
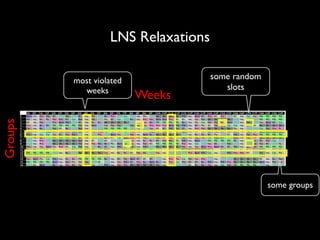
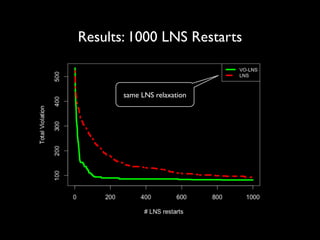
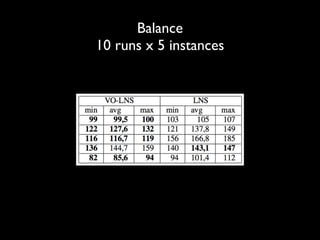
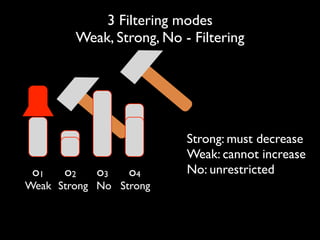
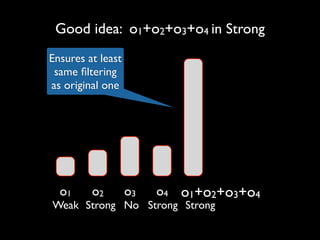
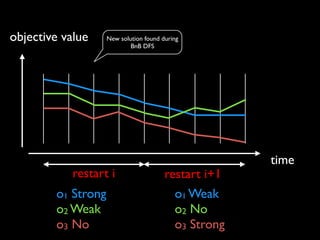
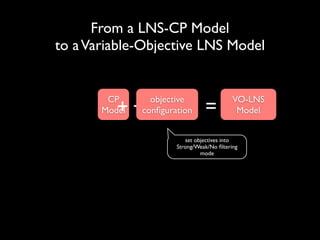
The document discusses a method called Variable Objective Large Neighborhood Search (VO-LNS) aimed at solving over-constrained problems by dynamically adjusting objectives at each restart to improve search efficiency and balance violations. It highlights the limitations of traditional Constraint Programming (CP) in minimizing violation sums and elaborates on experimental results demonstrating VO-LNS's superiority over standard LNS in various real-life timetabling applications. Future work is suggested to explore automatic objective configuration and expand the method to additional scheduling problems.
More Related Content
Similar to IACTAI13 Variable Objective Large Neighborhood Search: A practical approach to solve over-constrained problems (Pierre Schaus)
IACTAI13 Variable Objective Large Neighborhood Search: A practical approach to solve over-constrained problems (Pierre Schaus)
- 1. Variable Objective LargeNeighborhood Search: A practical approach to solve over-constrained problems Pierre Schaus UCL, ICTEAM, Belgium
- 2. Over-Constrained Problems Mon Tue Wed Usually renderthe problem over-constrained Demand >2 =2 gcc1 >1 >2 gcc2 >3 >1 gcc3
- 3. Relaxation = ViolationVariables in Constraints (Petit & Régin) Mon Demand >2 =2 Tue >1 >2 Wed >3 >1 o1) (...,o2) (...,o3) (..., gcc -gcc oft-gcc oft oft s s s
- 4. Aggregation of violations • • Manypossibilities Most intuitive one: o1+o2+o3+...
- 5. Minimize sum ofviolation variables o1+o2+o3+... Desired Properties : A: o1+o2+o3+... should be small B: o1+o2+o3+... should be balanced not easy to reached with CP
- 6.
- 7. Weak filtering ofsum (bound-consistency) large BnB search tree small fraction of it is explored with DFS bad solutions
- 8. Solution = LargeNeighborhood Search LNS = LS using CP for neighborhood exploration
- 9. Decision Variables LNS (Shaw98) .. .. .. .. .. .. .. .. .. .. .. .. Bound = 100 1 3 5 6 2 9 1 8 3 1 0 4 Find Initial Solution with CP
- 10. LNS (Shaw 98) .. .. .... .. Bound = 100 1 3 5 6 2 9 1 8 3 1 0 4 Relax* (randomly) this solution *aka fragment selection
- 11. LNS (Shaw 98) 7 .. 8 .. 14 .. .. 3 .. Bound = 96 1 3 5 6 2 9 1 8 3 1 0 4 Optimize this partial solution with CP
- 12. LNS (Shaw 98) .. .. .. .... Bound = 96 1 3 7 6 2 8 1 8 1 4 0 3 relax randomly
- 13. LNS (Shaw 98) ..7 2 .. .. 8 9 .. 1 4 1 3 .. 3 .. .. .. Bound = 85 1 3 5 6 2 10 1 8 3 1 0 4 re-optimize
- 14.
- 15. From a CPModel to a LNS Model CP Model + Relaxation Procedure = LNS Model Which decision Variables should be relaxed for next restart
- 16. Minimize sum ofviolation variables o1+o2+o3+... Desired Properties : A: o1+o2+o3+... should be small B: o1+o2+o3+... should be balanced
- 17. o1+o2+o3+o4 = 7 4 1 2 2 2 1 1 1 o1o2 o3 o4 o1 o2 o3 o4 balanced unbalanced How to avoid this ?
- 18. Dynamically Change theObjective (at each LNS restart)
- 19. Focus on worseobjective at each LNS restart ! o1 o2 o3 o4
- 20. Focus on worseobjective at each LNS restart ! o1 o2 o3 o4
- 21. Focus on worseobjective at each LNS restart ! o1 o2 o3 o4
- 22. Focus on worseobjective at each LNS restart ! o1 o2 o3 o4
- 23. In practice … • Objectiveconfiguration changed at each LNS restarts. • Each objective can be configured differently Strong = must decrease Weak = cannot increase No = unrestricted filtering
- 24. 3 Filtering modes Weak,Strong, No - Filtering ! ! o1 o2 o3 o4 Weak Strong No Strong Strong: must decrease Weak: cannot increase No: unrestricted
- 25. Good idea: o1+o2+o3+o4in Strong Ensures at least same filtering as original one o1 o2 o3 o4 o1+o2+o3+o4 Weak Strong No Strong Strong
- 26. objective value New solutionfound during BnB DFS restart i o1 Strong o2 Weak o3 No restart i+1 o1 Weak o2 No o3 Strong time
- 27. From a LNS-CPModel to a Variable-Objective LNS Model CP Model objective Relaxation configuration Procedure ++ = VO-LNS LNS Model Model set objectives into Strong/Weak/No filtering mode
- 28. Experimental Result • • Artificial over-constrainedproblems Over-Constraint timetabling application
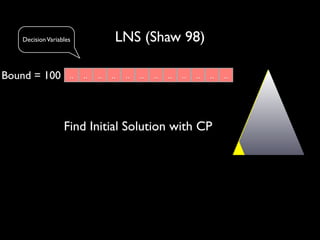
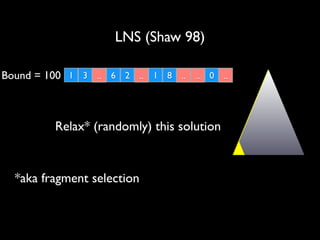
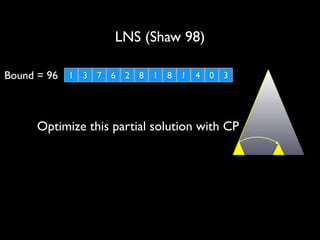
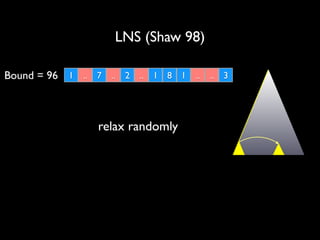
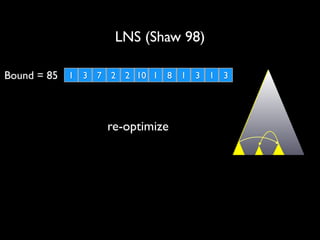
- 29. Artificial Over-Constrained Problem RandomDomain: 5 values on [1..15] oj every values 1..15 should appear exactly once on each row oi violation = sum of excess & shortage of each value every values 1..15 should appear exactly once on each column
- 30. LNS Relaxations R1 R2 10% ofvariables (randomly) = 10% of variables (randomly) + most violated line/column oi most violated line* *tabu mechanism for diversification
- 31. Objective Configurations o1 ,o2 , ... , o15 , o16 , ... , o30 , otot C1 C2 o1 , o2 , ... , o30 : No otot : Strong o1 , o2 , ... , o30 : Weak Standard minimization of sum, does not try to balance violations otot : Strong, oi: Strong The most violated row/column in current solutions oi
- 32. Experiments LNS 400 Restarts,50 Failure Limit ! • • • Setting A: R1 & C1 • random relax, standard minimization Setting B: R2 & C1 • structured relaxation, standard minimization Setting C: R2 & C2 • structured relaxation, variable objective (VO-LNS)
- 33. LNS VO-LNS Decrease faster & better sumof violations
- 34. Balancing Property Better total violation Bettertotal balancing VO-LNS
- 35. Real Life -Timetabling Hospitality Management School Groups Weeks
- 36. Real Life -Timetabling Hospitality Management School Groups Weeks Groups of 20 students must be scheduled over semester
- 37. Real Life -Timetabling Hospitality Management School PM Weeks Groups AM Two activities/ Week to decide Morning & Afternoon
- 38. Real Life -Timetabling Hospitality Management School Weeks Groups > 2x A1 = 1x A2 … For each group: cardinality requirement on activity types
- 39. Real Life -Timetabling Hospitality Management School Weeks Groups A1 is scheduled only 4 consecutive times, … Restriction on activity patterns
- 40. Real Life -Timetabling Hospitality Management School Weeks Groups A1 scheduled between 2 and 3 times A2 scheduled between 1 and 2 times … soft-gcc Demand over activities specific for each weak
- 41. Real Life -Timetabling Hospitality Management School Violations of cardinality requirements
- 42. LNS Relaxations Weeks some random slots Groups mostviolated weeks some groups
- 43. Results: 1000 LNSRestarts same LNS relaxation
- 44. VO-LNS is faster Why? number of exhausted search ! Because most of the LNS searches complete before the failure limit
- 45. Balance 10 runs x5 instances
- 46. Open-Source Implementation OscaR SCALA INOPERATIONAL RESEARCH https://bitbucket.org/oscarlib/oscar
- 47. Take away messages • Minimizingsum objective (in over-constrained problems) with CP is hard • • LNS is powerful to diversify search space Changing dynamically the objective can • • Fasten and improve LNS Better balance violations variable objective LNS
- 48. Future Work • • • Automatic objectiveconfiguration Population of solutions (different configurations) More problems (just in time scheduling)
- 49. Variable Objective LargeNeighborhood Search: A practical approach to solve over-constrained problems Pierre Schaus UCL, ICTEAM, Belgium