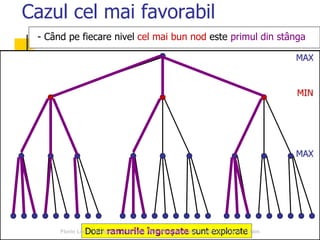
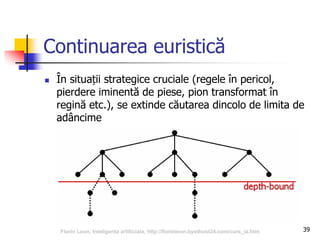
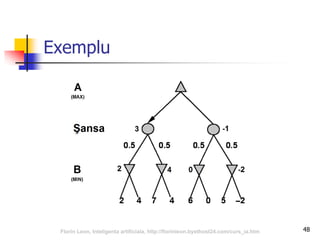
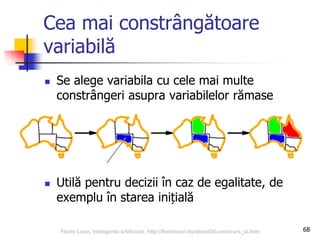
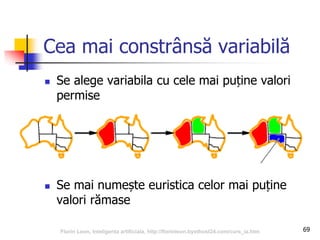
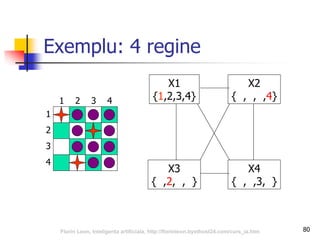
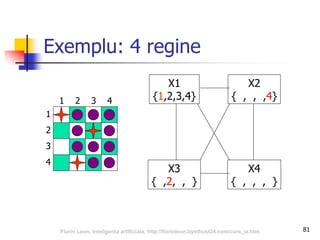
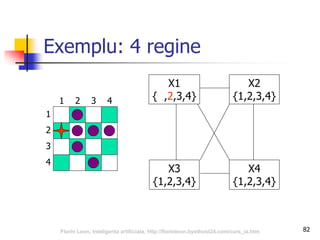
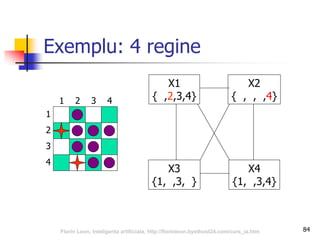
Documentul abordează relația dintre inteligența artificială și jocuri, subliniind importanța acestora în dezvoltarea algoritmilor de AI. Se discută despre tipurile de jocuri, tehnici de căutare precum algoritmul minimax și optimizarea prin tăierea alfa-beta, precum și despre evaluarea pozițiilor în joc. Concluziile sugerează că jocurile reprezintă provocări semnificative pentru AI datorită complexității și mărimii spațiului de căutare.















![16
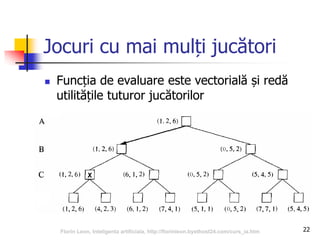
Exemple: funcții de evaluare
X și 0:
f(n) = [numărul de direcții de 3 pătrățele deschise pentru
calculator] – [numărul de direcții deschise pentru adversar]
Direcțiile sunt linii, coloane sau diagonale complete
Șah (funcția lui Turing):
f(n) = w(n) / b(n)
w(n) = suma punctelor pieselor albe
b(n) = suma punctelor pieselor negre
Pion = 1 punct, cal/nebun = 3 puncte, turn = 5 puncte,
regină = 9 puncte
Florin Leon, Inteligenta artificiala, http://florinleon.byethost24.com/curs_ia.htm](https://image.slidesharecdn.com/ia03jocuricsp-170510090529/85/Jocuri-Satisfacerea-constrangerilor-16-320.jpg)