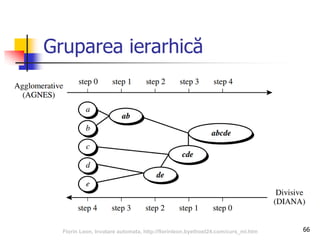
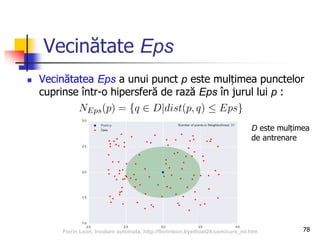
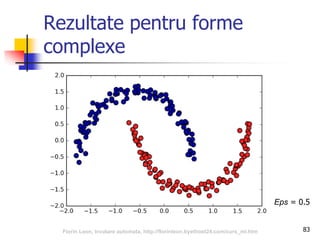
Documentul se concentrează pe algoritmi de grupare în învățarea automată, incluzând k-means, EM, gruparea ierarhică și DBSCAN. Se discută despre conceptele de clasificare, regresie și reguli de asociere în cadrul învățării automate, evidențiind importanța învățării din experiență. De asemenea, sunt prezentate probleme întâmpinate de algoritmi, metode de determinare a numărului de grupuri și măsuri de calitate a grupării.






![Învățarea automată
engl. “machine learning”
Își propune găsirea automată a unor modele
interesante în date
Direcții principale:
Clasificarea și regresia
Gruparea (clustering [clástering], partiționare,
clusterizare [clasterizáre])
Determinarea regulilor de asociere
Selecția trăsăturilor
8Florin Leon, Invatare automata, http://florinleon.byethost24.com/curs_ml.htm](https://image.slidesharecdn.com/ml01clusterizare-170510092302/85/Algoritmi-de-grupare-clustering-8-320.jpg)










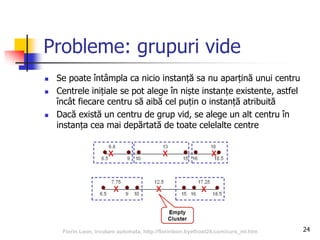



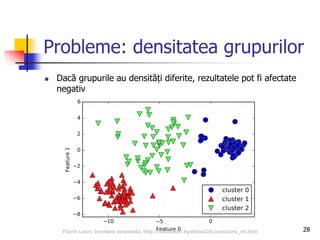
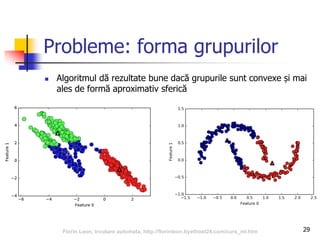
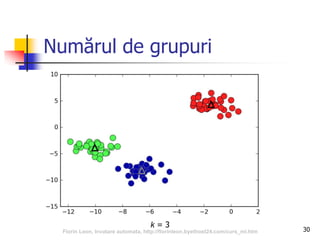


![35
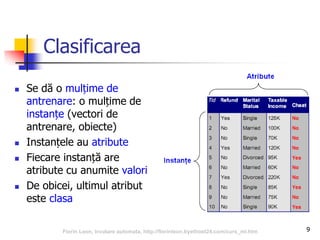
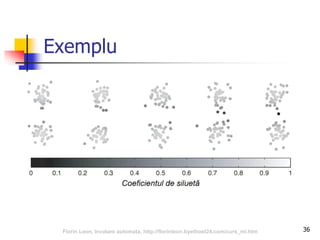
Calcularea coeficientului de
siluetă
Pentru o instanță, se calculează:
ai – distanța medie față de instanțele din același grup
bi – distanța minimă față de orice instanță din orice alt grup
Coeficientul de siluetă al instanței i este:
si = (bi – ai) / max(ai, bi) [-1, 1]
Gruparea este mai bună când si este mai mare,
aproape de 1 (ai ≪ bi)
Coeficientul de siluetă al unui grup este media
coeficienților instanțelor
Florin Leon, Invatare automata, http://florinleon.byethost24.com/curs_ml.htm](https://image.slidesharecdn.com/ml01clusterizare-170510092302/85/Algoritmi-de-grupare-clustering-35-320.jpg)



![Funcție de densitate de
probabilitate
Care este probabilitatea de a ghici un număr natural
generat aleatoriu uniform din intervalul [1, 5]?
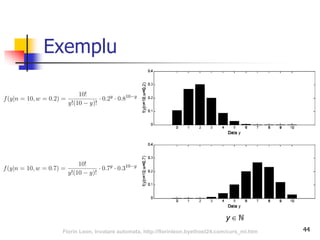
x = numărul generat, y = numărul ghicit
P(y = x) = 1/5, x { 1, 2, 3, 4, 5 }
Care este probabilitatea de a ghici un număr real
generat aleatoriu uniform din intervalul [1, 5]?
Există o infinitate de numere reale în acest interval
P(y = x) = 0, x [1, 5]
40Florin Leon, Invatare automata, http://florinleon.byethost24.com/curs_ml.htm](https://image.slidesharecdn.com/ml01clusterizare-170510092302/85/Algoritmi-de-grupare-clustering-40-320.jpg)
![Funcție de densitate de
probabilitate
Se poate calcula totuși probabilitatea ca y să aparțină
unui subinterval
P(y [1, 2]) = 1/4
P(y [1, 5]) = 1
În general:
unde ρ este funcția de densitate de probabilitate,
FDP (engl. “probability density function”, PDF)
41Florin Leon, Invatare automata, http://florinleon.byethost24.com/curs_ml.htm](https://image.slidesharecdn.com/ml01clusterizare-170510092302/85/Algoritmi-de-grupare-clustering-41-320.jpg)