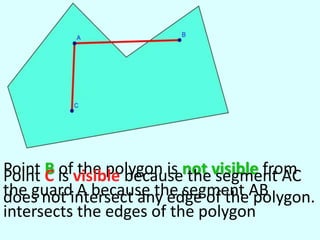
This document discusses the art gallery problem in computational geometry, which aims to determine the minimum number of guards needed to monitor an art gallery or museum. It provides context about the problem being raised by Victor Klee in 1973 and first solved by Václav Chvátal in 1975, who determined that n-3 guards are always sufficient and sometimes necessary to guard a simple polygon with n vertices. The document then explains concepts like visibility, triangulation strategies, and dual graphs that are relevant to solving the art gallery problem.

5. The art gallery problem or
museum problem is a visibility
problem in computational
geometry.
The problem was raised
by Victor Klee in 1973

6. The question we need to answer is:
How many guards are needed (the
sufficient and necessary number) and
so they will keep all
together, any part of the museum P at any
time.

10. A guard sees any point of the museum, if
the segment line defined by the point and
the guard does not intersect any of the
edges of the polygon.
Visibility of a
guardian

11. Point B of the polygon is not visible from
the guard A because the segment AB
intersects the edges of the polygon
Point C is visible because the segment AC
does not intersect any edge of the polygon.

12. Therefore we say that a room (hall) is
been guarded, when any interior point
of it, is visible from at least one guard.

13. Václav Chvátal gave a first
solution to the problem in
1975.
He states that
are always sufficient
and sometimes
necessary to guard a
simple polygon with n
vertices.
guards

16. The Visual Module
Vpython, Version 5.72
gives the limit of Chvátal, using the
method proposed by Fisk.

17. The polygon
P is convex
so, the
minimum
number of
guards is 1.
The polygon is non convex
so, the minimum number
of guards is calculated
through the algorithm
with the program of The
Visual Module Vpython.

18. The triangulation strategy
The partition of a polygon into triangles is a
method called triangulation.
Triangulation of a polygon is called a set of
triangles with the following properties:
The triangles are defined by the vertices
of the polygon.
The sum of triangles is equal to the
polygon.
Any two triangles either do not intersect,
or have a common vertex, or a common
edge.

19. The dual graph is a
structure consisting of
entities and relationships
that are formulated with
points and edges.
Dual
Graph