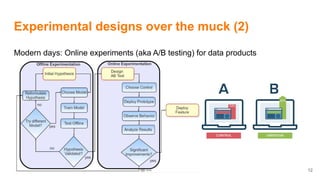
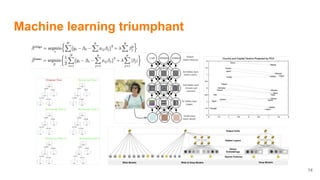
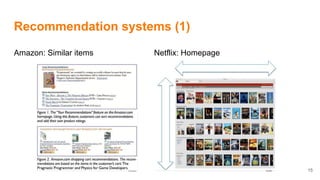
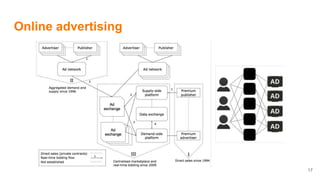
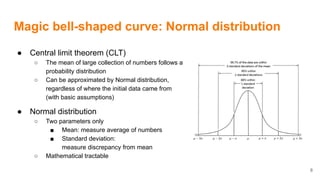
The document discusses how data science and machine learning have transformed scientific approaches and methodologies, illustrated through the historical anecdote of 'The Lady Tasting Tea' which highlights experimental design and hypothesis testing. It emphasizes two revolutions in science: the shift from a clockwork universe to a statistical one, where randomness and probability play critical roles in understanding data. The author also addresses the applications of machine learning in various domains, including recommendation systems and natural language processing.

1. The Lady Tasting Tea and Further Beyond
- How Data Science / Machine Learning is Revolutionizing World
Bowen Li
Software Engineer, Machine Learning
2020/08/28

2. Great book recommendation
“The Lady Tasting Tea: How Statistics Revolutionized Science” by David Salsburg
2

3. Outline
● Two Revolutions in Science
● The Lady Tasting Tea
● Probability Distributions
● Magic Bell-Shaped Curve: Normal Distribution
● Hypothesis Testing & Confidence Interval Tricks
● Experimental Designs over the Muck
● Machine Learning Applications Are Everywhere
● Anyway, What’s Data Scientist?
3

4. Two revolutions in science (1)
● Chaotic universe: before 19th century
● 1st revolution in science: clockwork universe
○ Small number of mathematical formulas could be used to
■ interpret reality
■ predict future events
○ Laplace replied to Napoleon:
“I had no need for that hypothesis [for God].”
○ A proof in 1840:
Newton's laws were used to predict the existence of the planet Neptune
○ Still need error function: sum all the errors up
■ Scientists believed with more precise measurements,
the need for error function will diminish (but not!)
4

5. Two revolutions in science (2)
● 2nd revolution in science: statistical universe
○ With more and more precise measurements,
more and more error cropped up
○ Fails in finding laws of biology and sociology
○ Randomness is everywhere
● So, what’s statistics?
○ A methodology to find out rules / associations from
out-of-order data, which is messed up by randomness
● Starting point?
○ Good idea: from the story of the lady tasting tea :-)
5

6. The lady tasting tea
It was a summer afternoon in Cambridge, England,
in the late of 1920...
● A lady insisted: tea tasted different depending upon
○ whether the tea -> the milk or
○ whether the milk -> the tea
● Fisher said excitedly, “Let us test the proposition!”
● Real or fictious story?
○ Fisher wrote the story in his book: “The Design of Experiments”,
but did not mention the results
○ It’s a real story, and the result is…
The lady identified every single cup correctly! :-)
6

7. Probability distributions
● Charles Darwin’s Theory of Survival of the Fittest
○ Proposed: “Changing environments gave a slight advantage to
those random changes that fit better into the new environment.”
● Karl Pearson at University of College London
○ Might not be able to live long enough to see a new species
○ But might be able to see a change in attribute’s probability distribution
● Finally…
○ Darwin's theory were shown to be true for short-lived species like bacteria / fruit flies
○ The remaining of Pearson’s theory:
what’s observable are probability distributions associated with observations
7

8. Magic bell-shaped curve: Normal distribution
● Central limit theorem (CLT)
○ The mean of large collection of numbers follows a
probability distribution
○ Can be approximated by Normal distribution,
regardless of where the initial data came from
(with basic assumptions)
● Normal distribution
○ Two parameters only
■ Mean: measure average of numbers
■ Standard deviation:
measure discrepancy from mean
○ Mathematical tractable
8

9. Hypothesis testing trick
● Null (H0) vs. alternative hypotheses (H1)
○ Suppose null hypothesis H0 is correct
■ would like alternative hypothesis H1 holds
■ innocence presumption:
accept H1 only if significant
○ Then calculate the probability of outcome
○ If the probability is small, reject null hypothesis!
● Type I vs. II Errors
9

10. Confidence interval trick
● Hemophilia patients’s mean latency time
○ Point estimate = 5.7 years; just a single number
○ Interval estimate = [3.7, 12.4] years
● Why confidence interval (CI)?
○ Strategies that would be required are about the same
for both ends of the interval estimate
● Interpretation
○ In the long run, the statistician using 95% CIs will
find that the true value of the parameter
lies within the computed interval 95% of the time.
○ NOT the probability that we are correct
10

11. Experimental designs over the muck (1)
● Sir Ronald Fisher on the lady tasting tea
○ If one cup of tea only, she may guess correctly
○ If she can identify, she may make mistake sometimes
○ Fisher proposed a experimental design on
■ how many cups of tea and
■ in what order
○ Then calculated the probability based on the results
● Experimental design
○ Needs to start with a mathematical model of the outcome
of the potential experiment
○ Then collect data from experiment and computes outcomes
● George Box:
○ “Block what you can control and randomize what you cannot” 11

12. Experimental designs over the muck (2)
Modern days: Online experiments (aka A/B testing) for data products
12

13. Machine learning applications are everywhere
13

14. Machine learning triumphant
14

15. Recommendation systems (1)
Amazon: Similar items Netflix: Homepage
15

16. Recommendation systems (2)
16
Zalando: Homepage Zalando: Similar items

17. Online advertising
17

18. Computer vision (CV)
Andrej Karpathy (2016)
18

19. Natural language processing (NLP)
19

20. ML applications to name a few…
20
Stitch Fix: Intelligent assignment Stitch Fix: Demand forecasting
Next purchase time

21. Anyway, what’s data scientist? (1)
21

22. Anyway, what’s data scientist? (2)
22

23. Anyway, what’s data scientist? (3)
23

24. Anyway, what’s data scientist? (4)
24

25. Thank You for Your Attention!
25