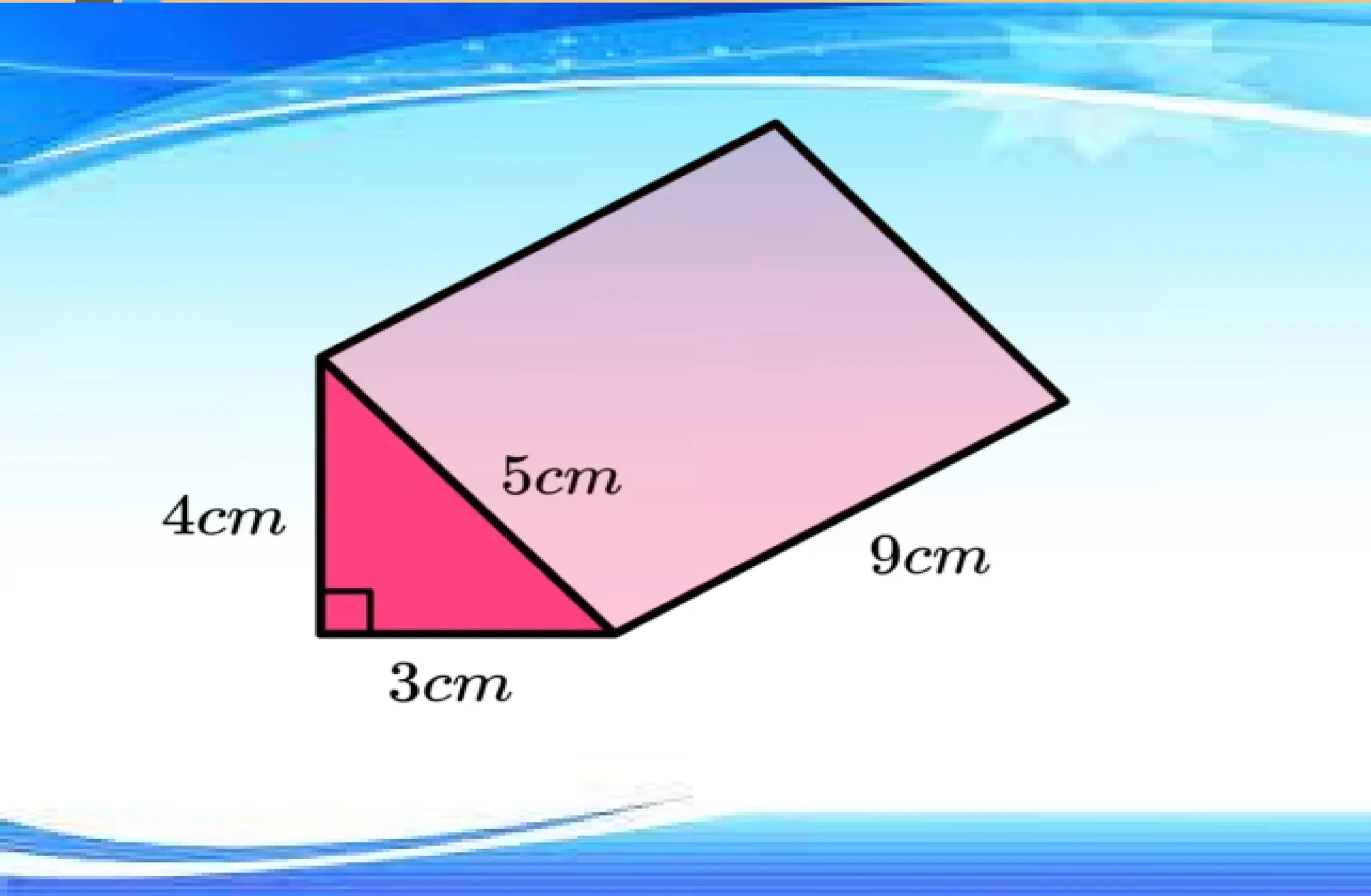
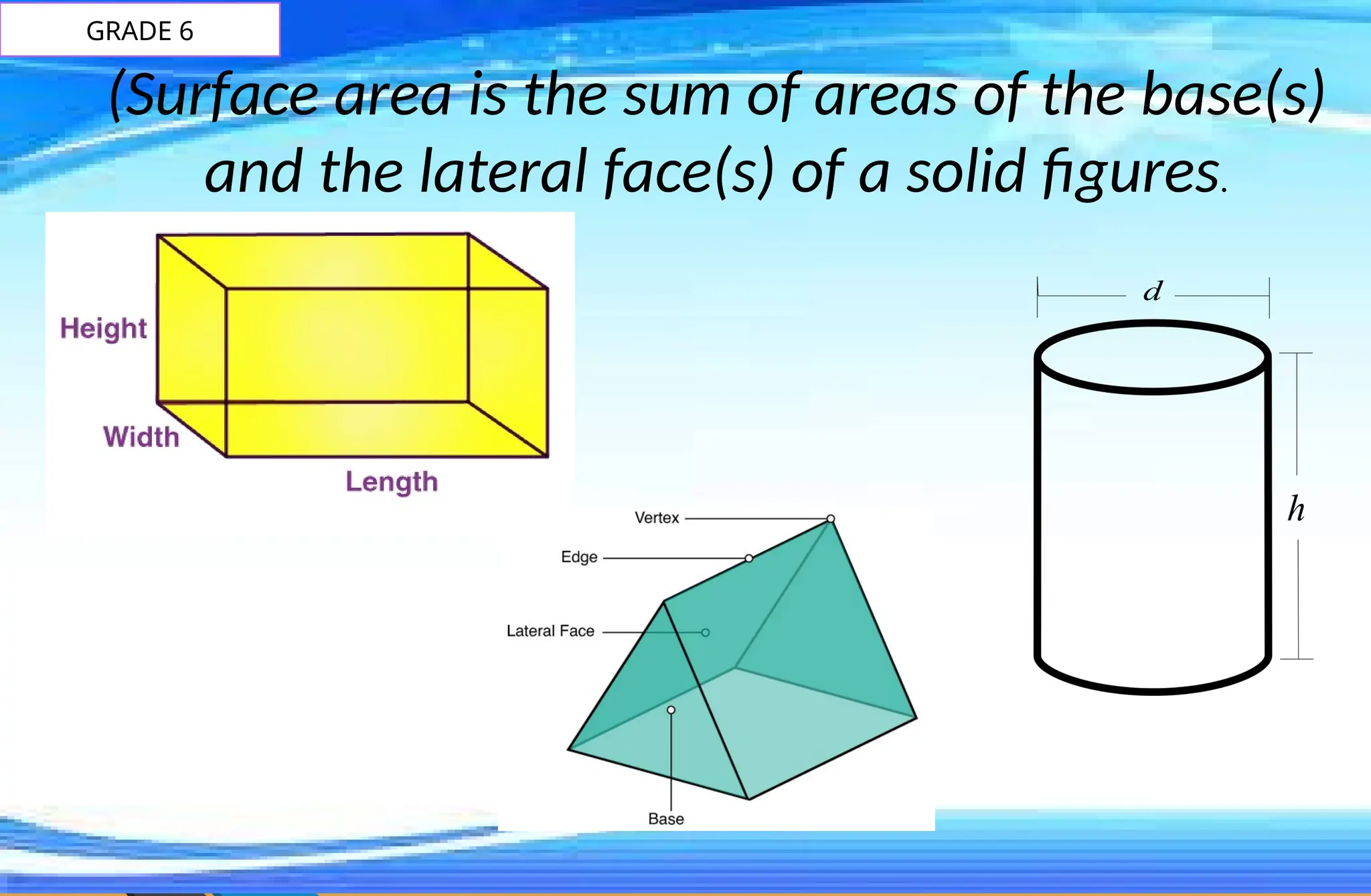
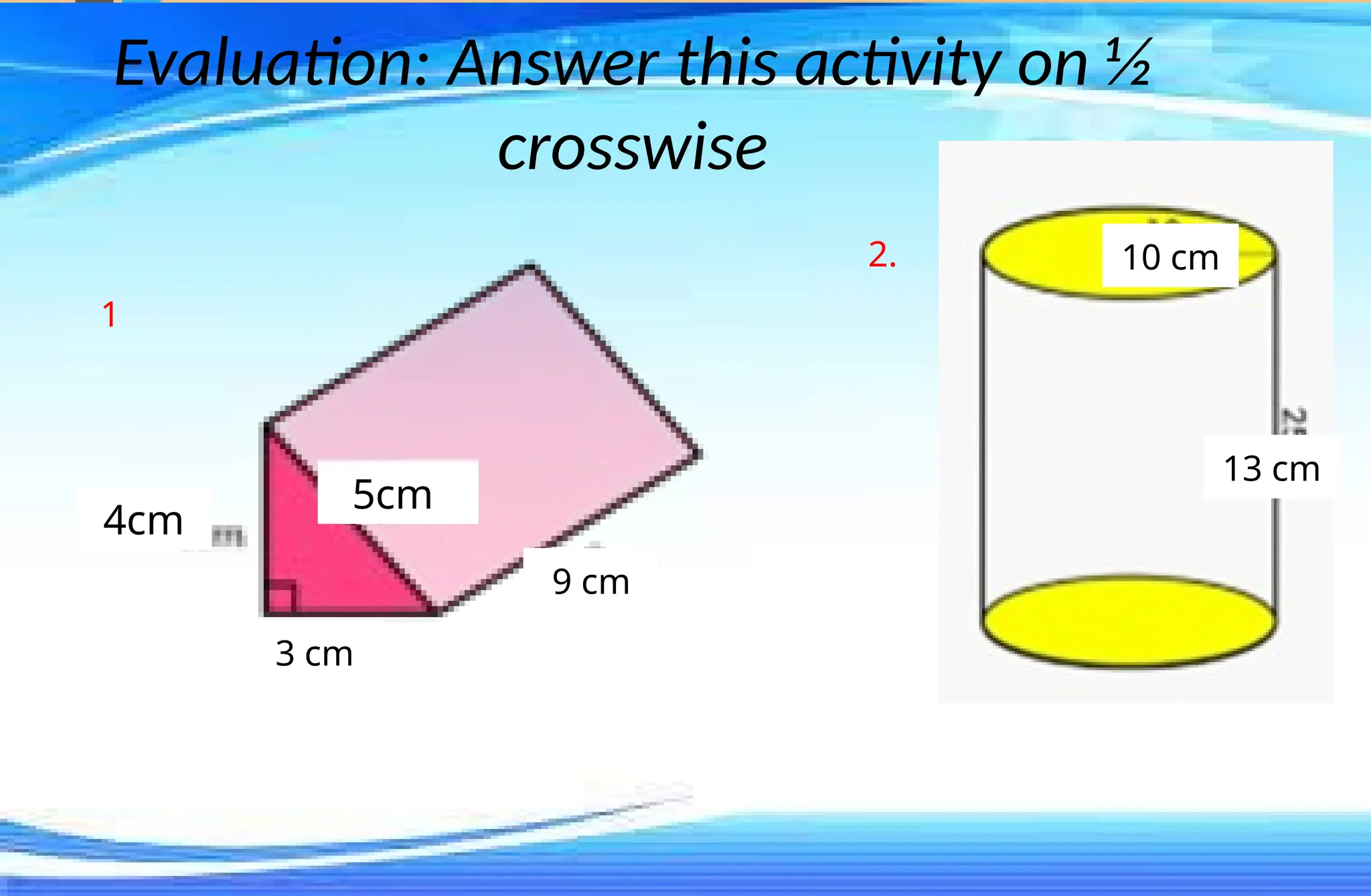
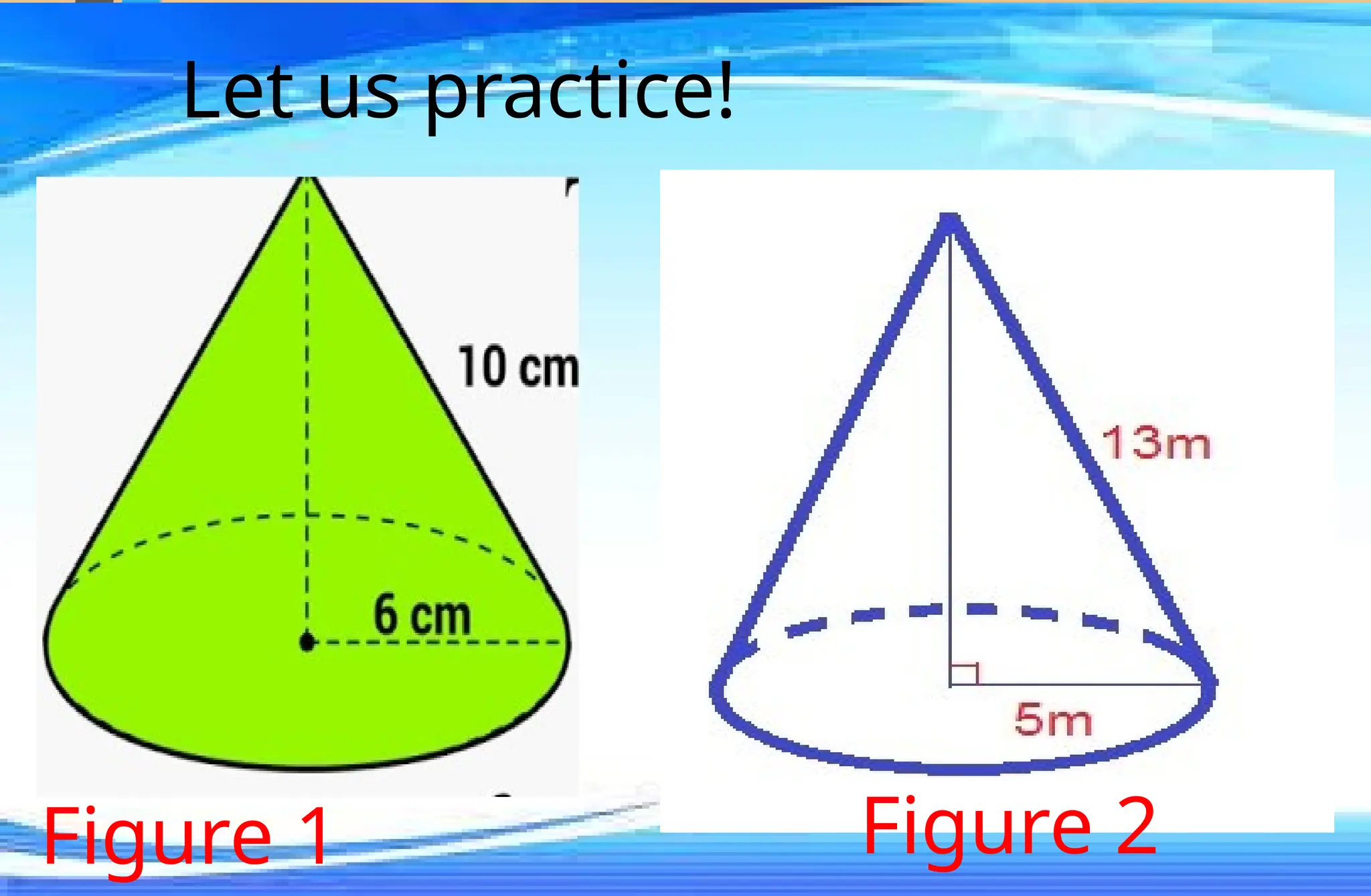
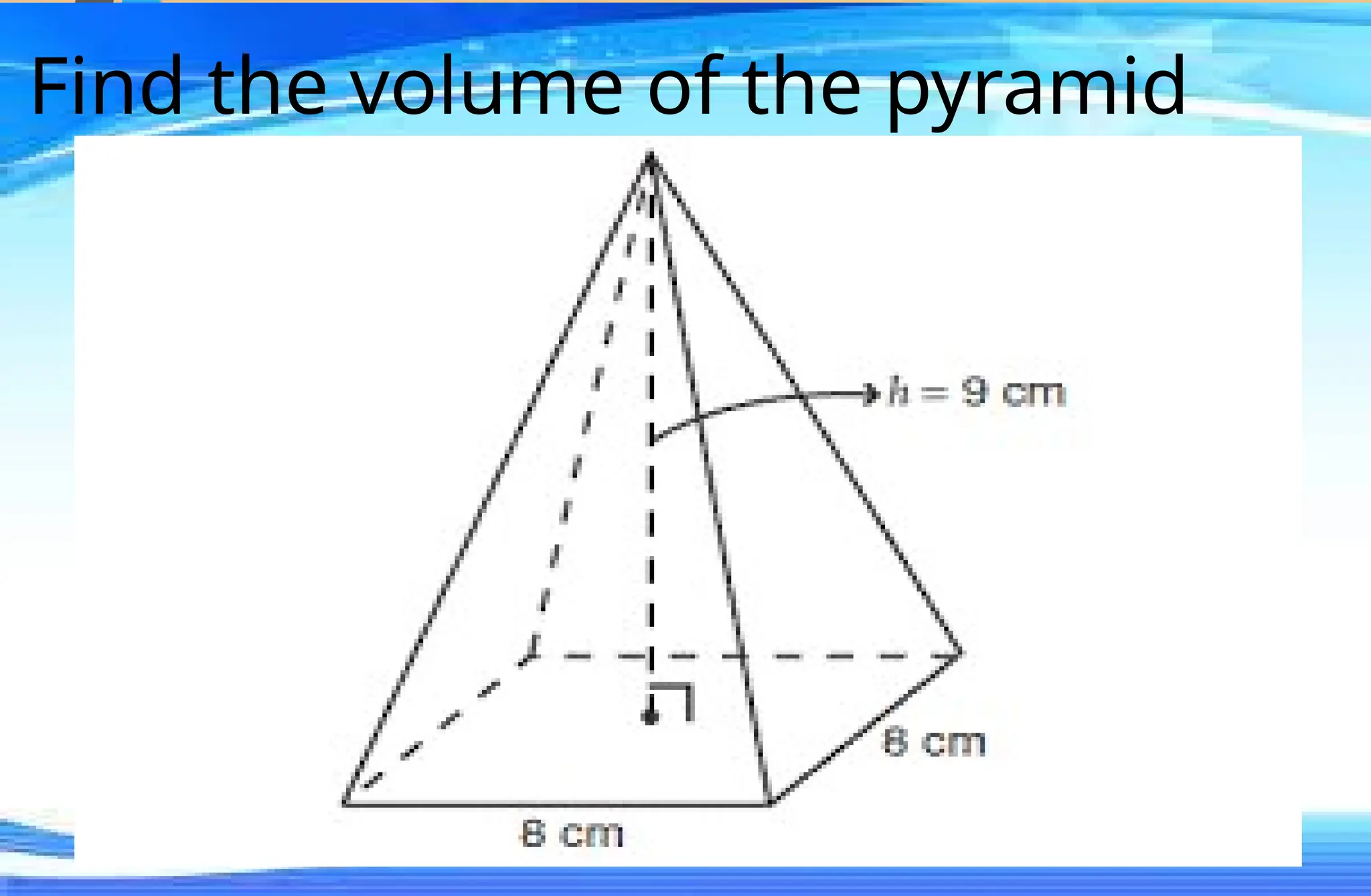
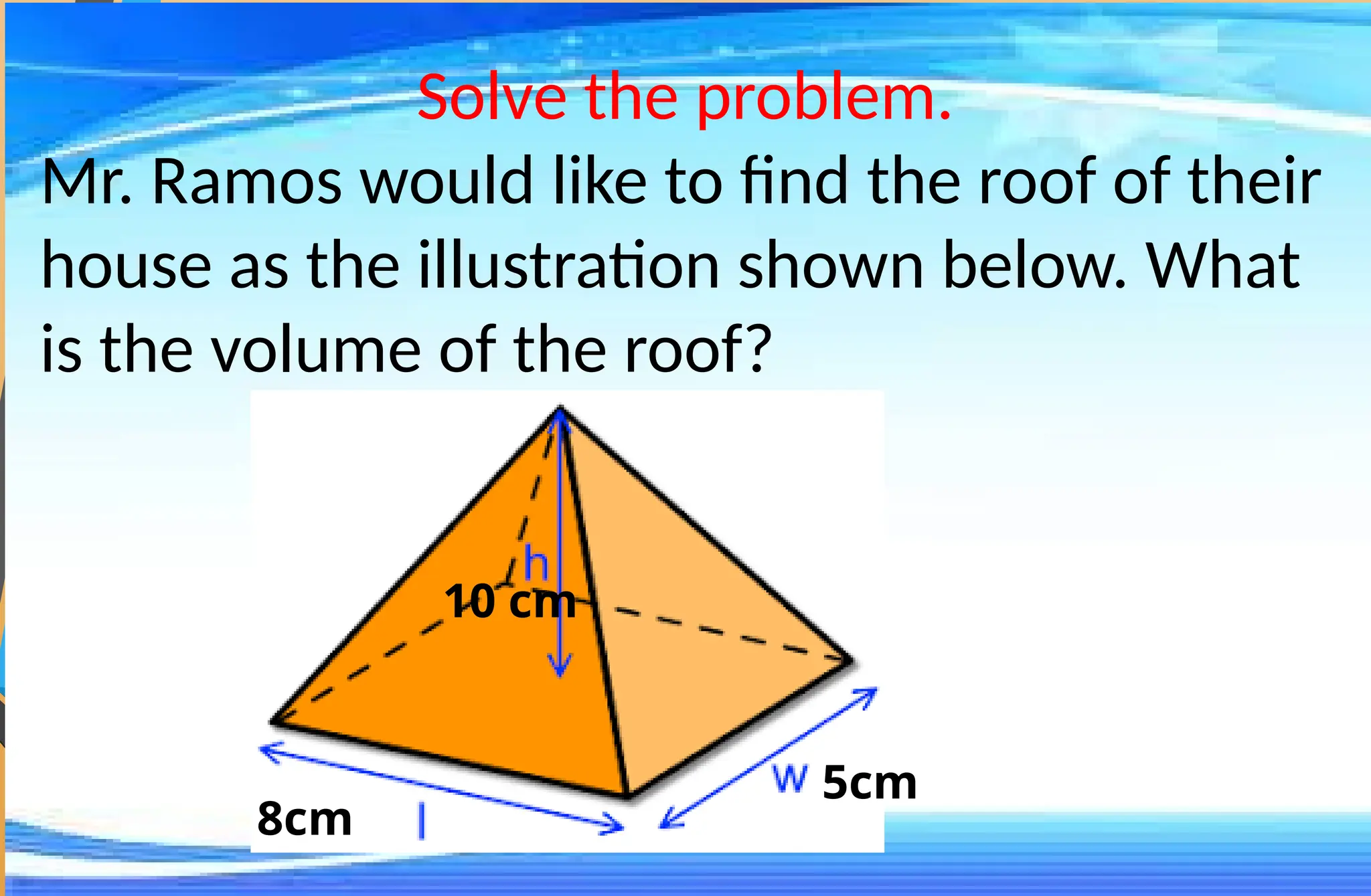
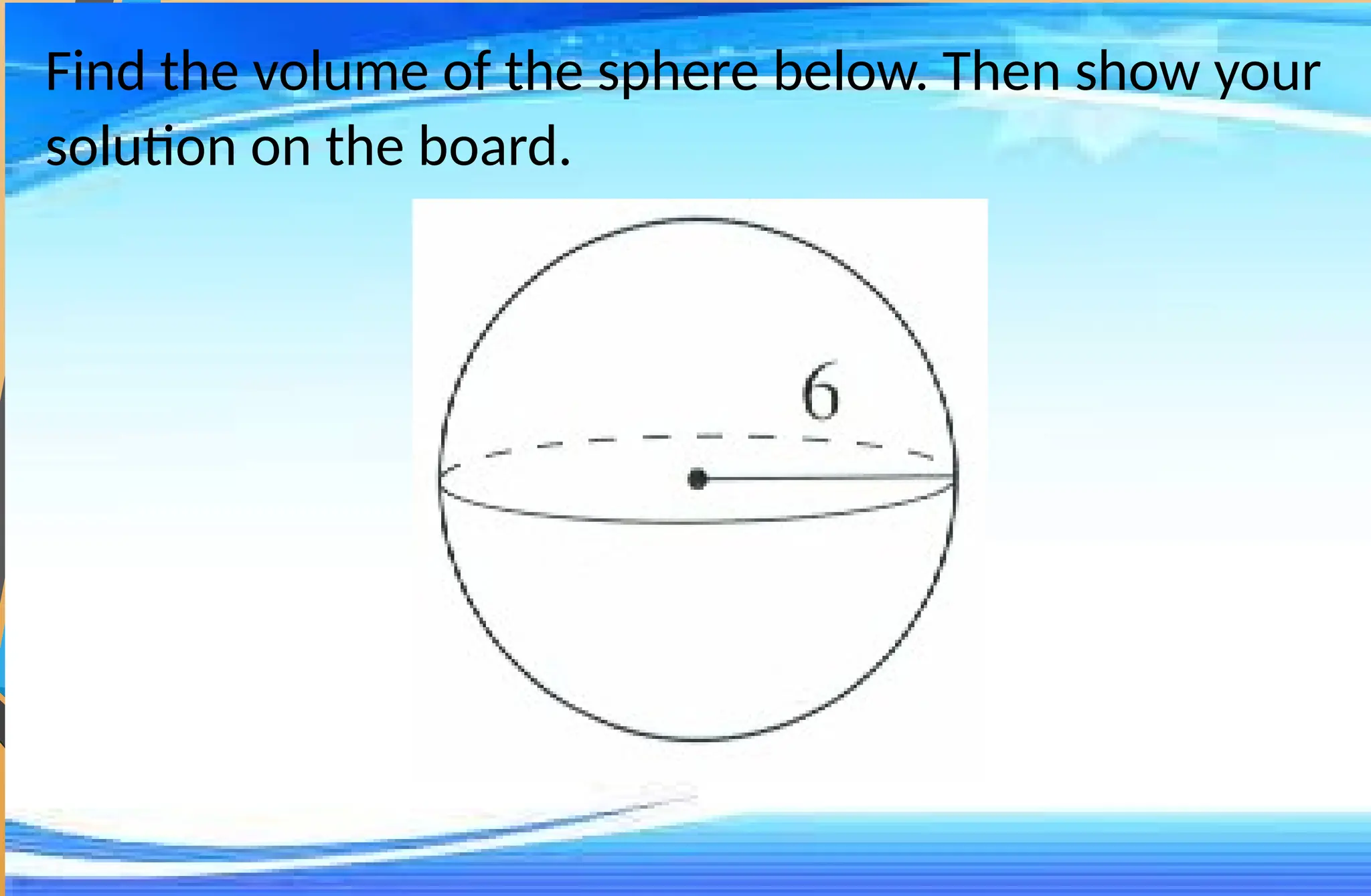
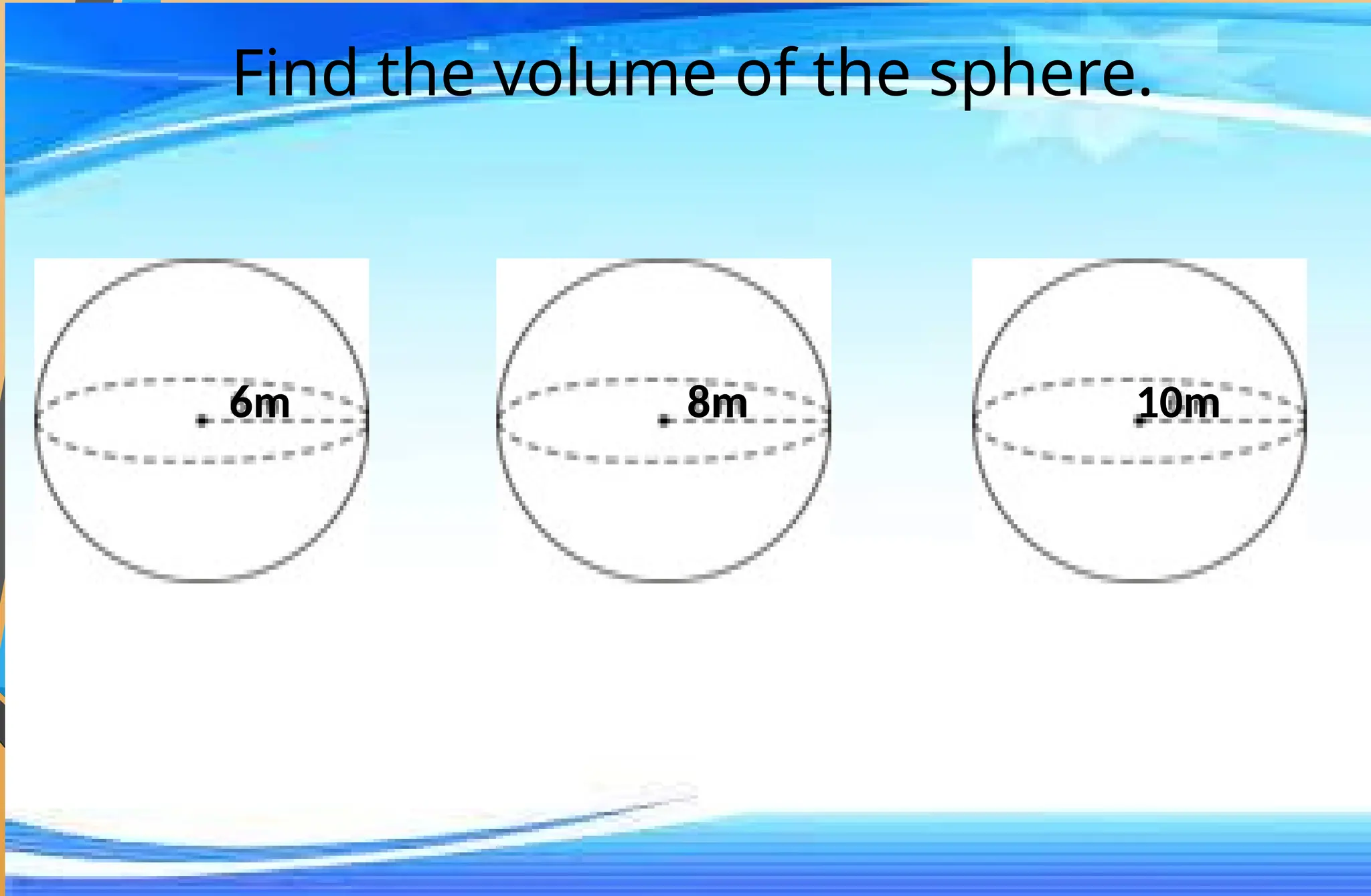
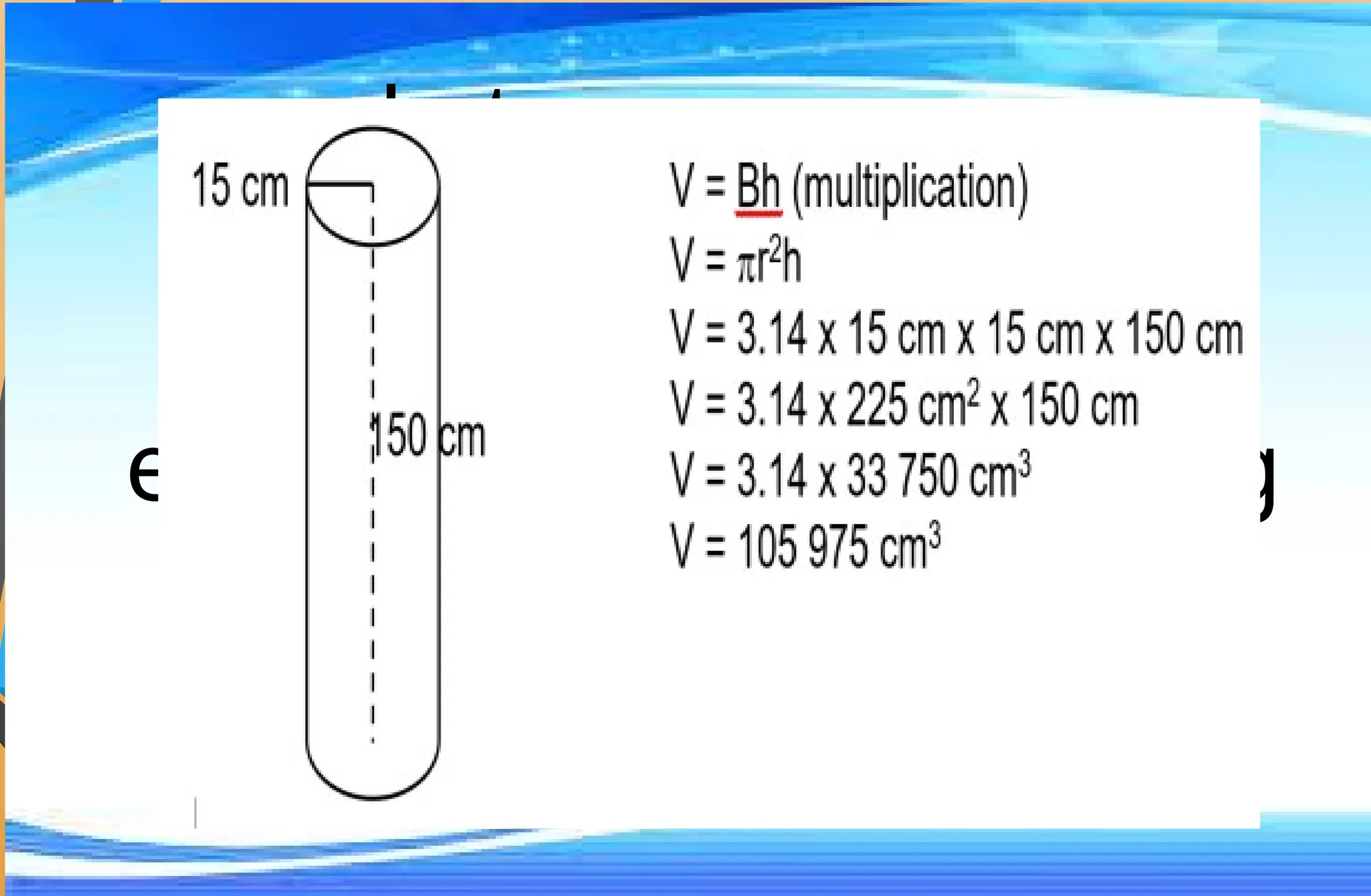
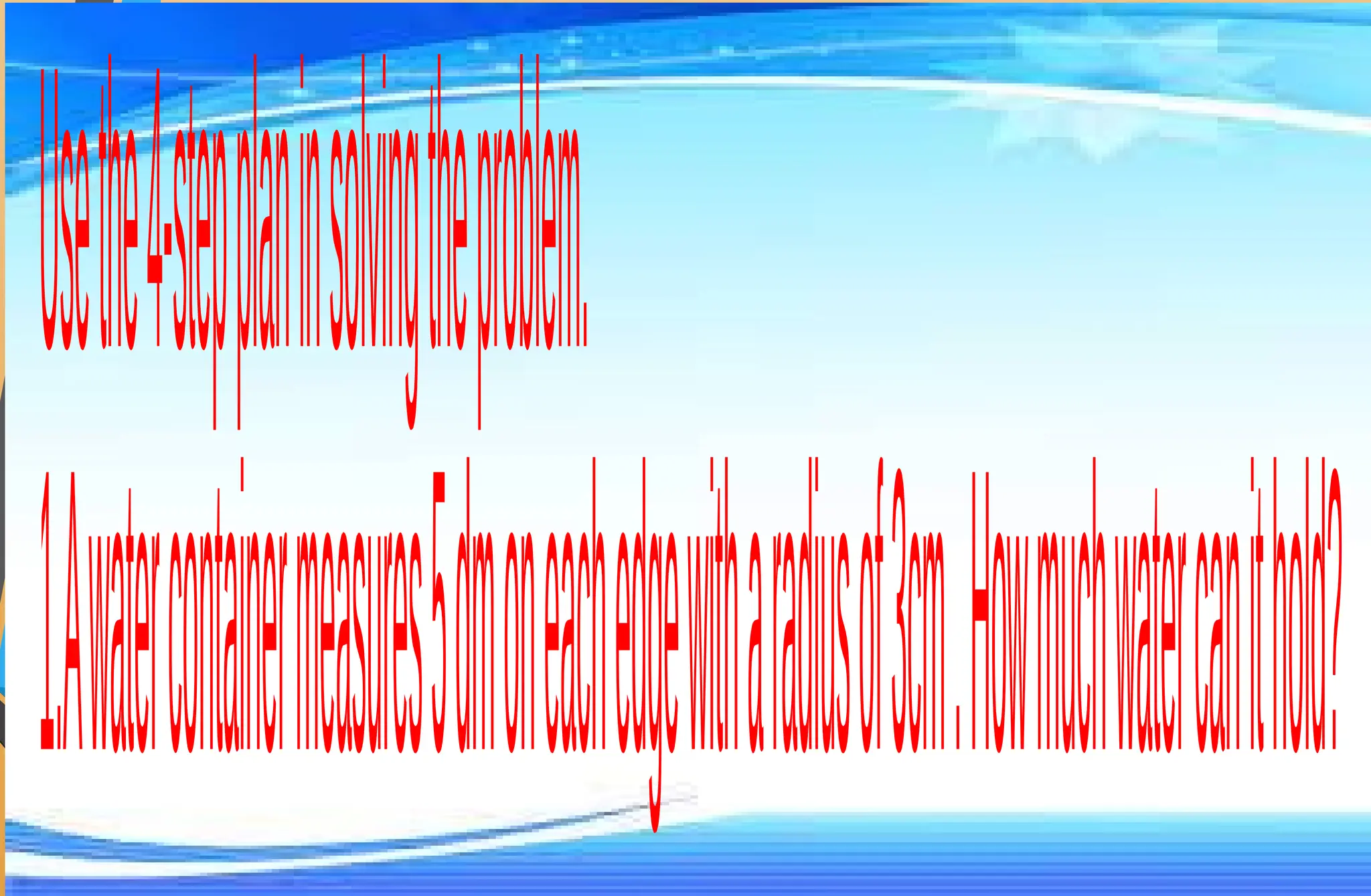
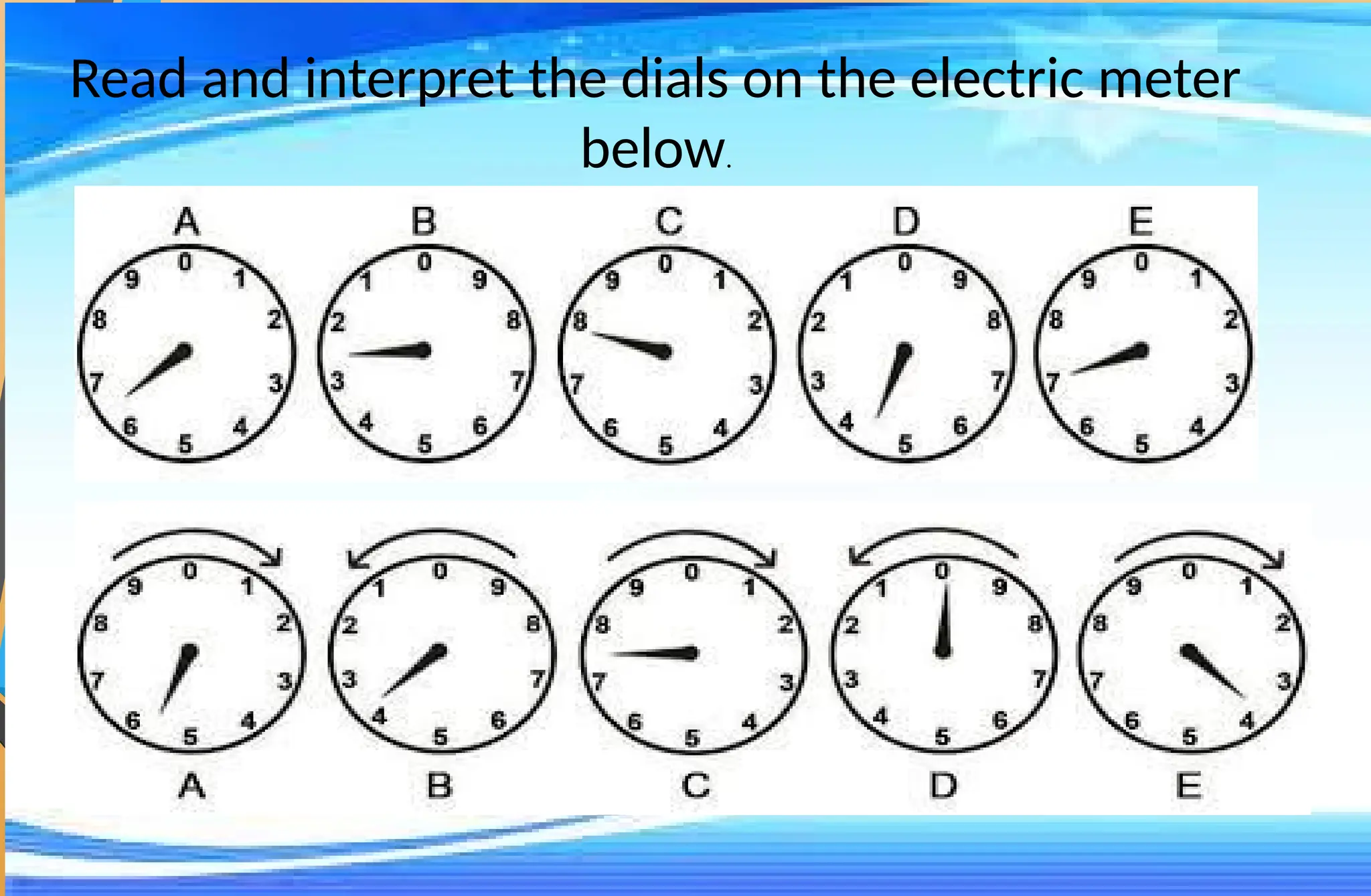
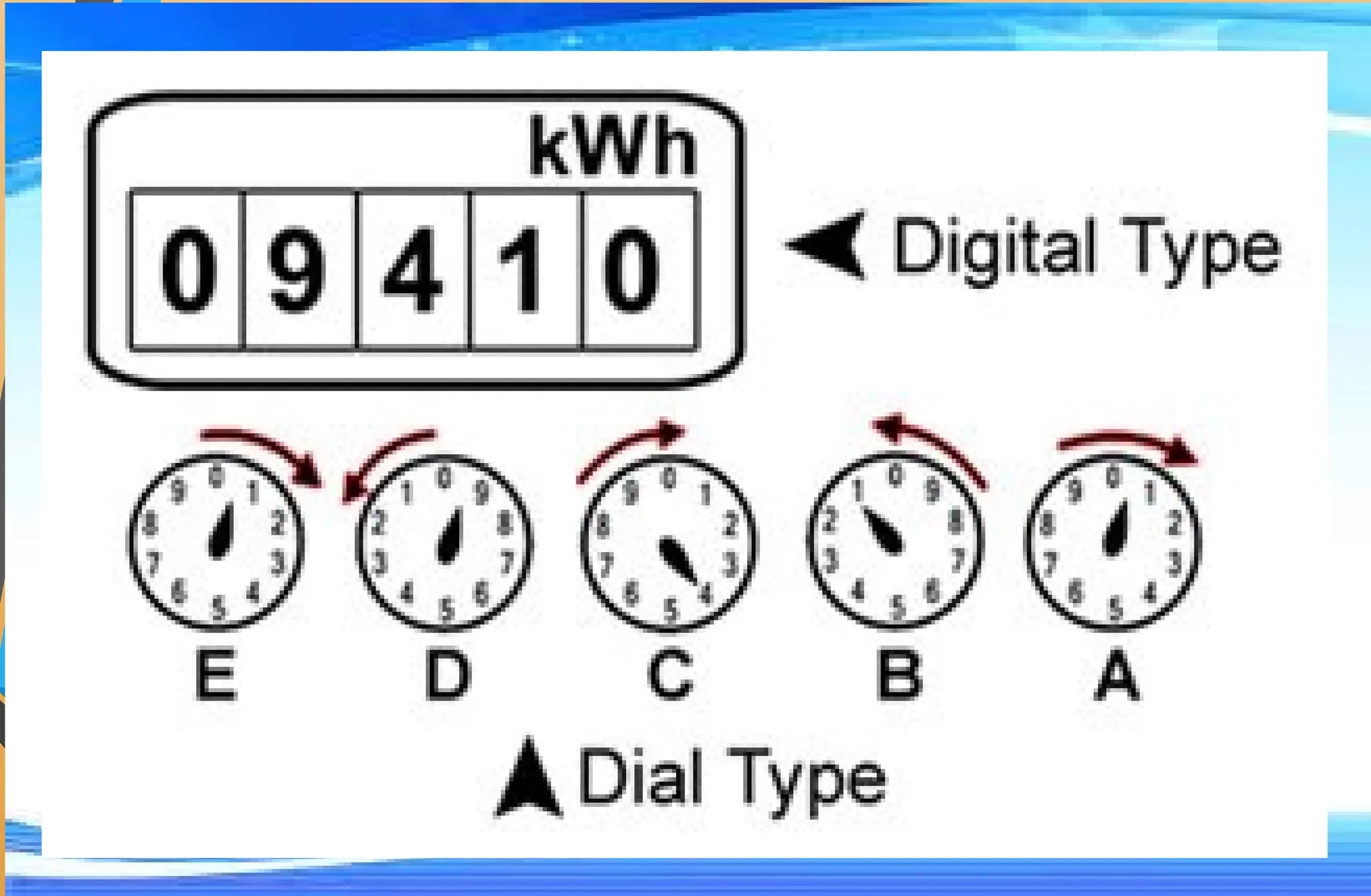
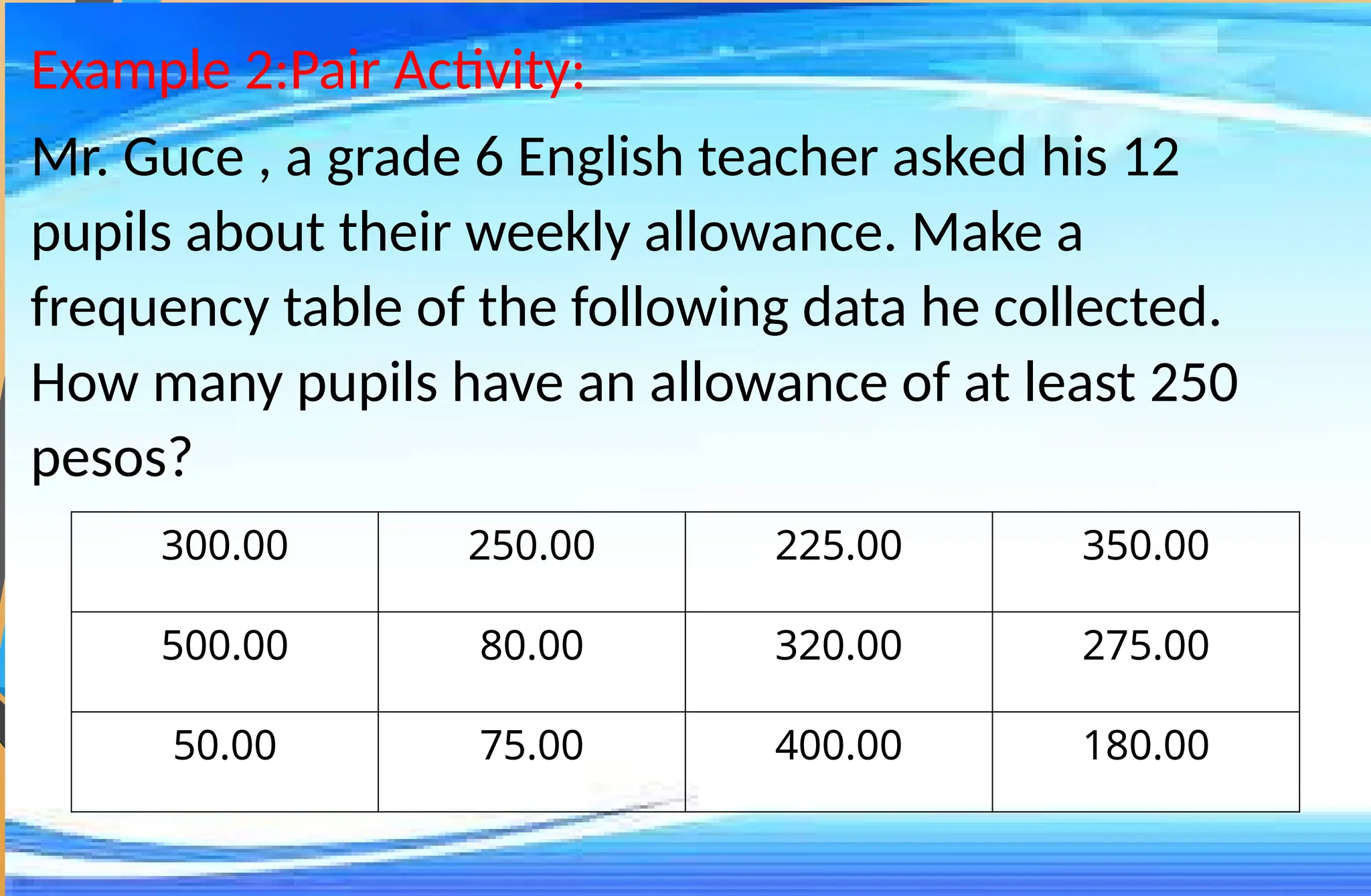
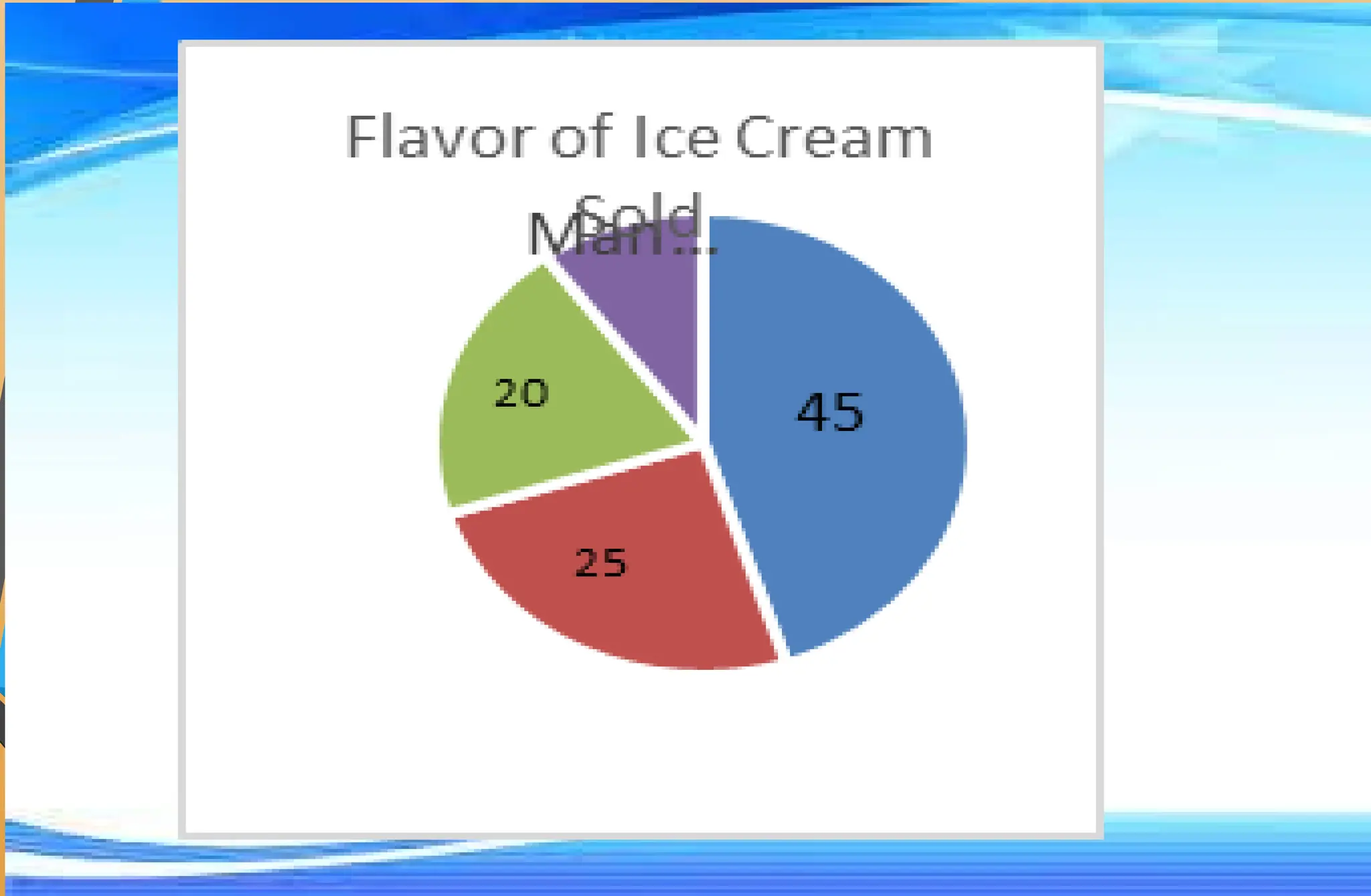
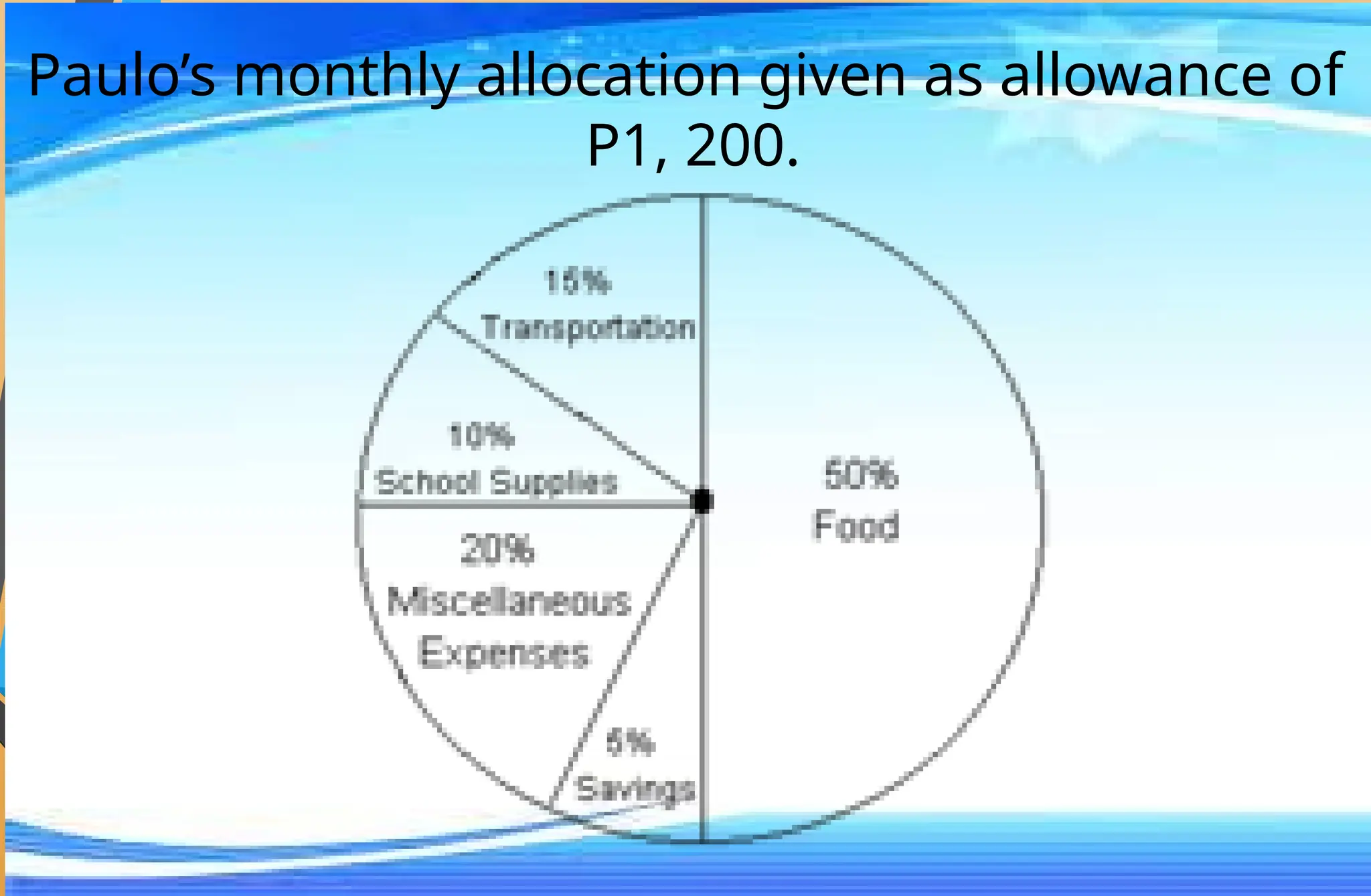
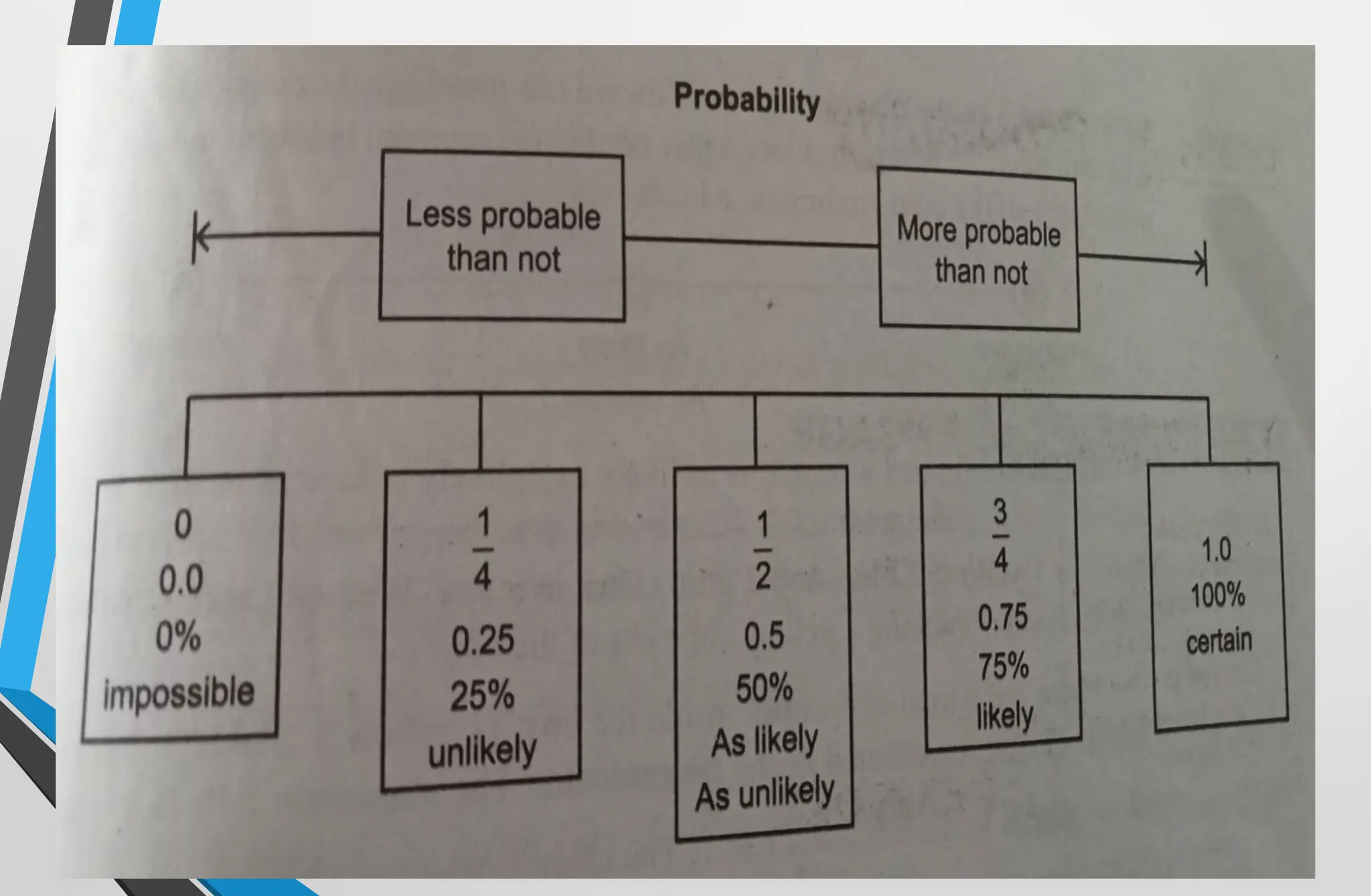
The document covers mathematical concepts related to surface area and volume of various geometric shapes, including cylinders, cones, pyramids, and spheres. It contains exercises and problem statements designed for students to practice calculating these measurements while also integrating real-life examples. Furthermore, it discusses the application of probability, data collection, and electric consumption analysis.

2. (Surface area is the sum of areas of the base(s)
and the lateral face(s) of a solid figures.
GRADE 6

3. Evaluation: Answer this activity on ½
crosswise
5cm
4cm
9 cm
3 cm
10 cm
13 cm
2.
1

5. What can you see in the pictures?

6. Give examples of pyramid that we see
in our daily life.

7. Direction: Find the surface area of the figures
below on your math notebook.
30m
20m 20m

8. What is this?
What figure is this?
Where do you see
this picture?
Give examples of
cone that we see in
our daily life.

10. Let us practice!
Figure 1 Figure 2

11. Find the surface area of the
problem below.
1.The roof is shaped like a cone
with the diameter of 12 feet. One
bundle of shingles cover 32 square
feet. How many bundles should
you buy to cover the roof.

12. Evaluation:
Direction: Find the
surface area of the
figures on your book on
page 284 numbers 38-
40 only on 1 whole

14. “The volume of a cylinder is the
amount of space inside the cylinder.
Finding the volume of cylinder is
similar to finding the volume of any
prism.”
Volume is defined as the space
occupied within the boundaries
of an object in three-dimensional
space. It is also known as the
capacity of the object.

15. Solve the volume of the cylinder.

16. The cylindrical Giant Ocean
Tank at the New England
Aquarium in Boston is 24
feet deep and has a radius of
18.8 feet. Find the volume of
the tank.

17. What is volume?
How to find the
volume of a cylinder?

18. What is the video all about?
Give examples of pyramid that
you see around?
What is the formula to find the
volume of a pyramid?

19. Look at the examples on your
book page 290.
Volume is measured in cubic
units which means it tell us how
many cubes of a given size it
takes to fill the pyramid.

20. Find the volume of the pyramid

21. Solve the problem.
Mr. Ramos would like to find the roof of their
house as the illustration shown below. What
is the volume of the roof?
8cm
5cm
10 cm

22. How do we find the volume of a prism

23. Find the volume of the
solid figures on page
296
Numbers 4 and 7 only.

24. What are examples of spheres found all
around us?
-The planet is a sphere.
-Basketballs and soccer balls are spheres
Give more examples of sphere.

25. A sphere is the set of all points that are
a given distance from a given point, the
center.
To calculate volume of a sphere, use the
formula: V= 4/3 x π r3
Volume is measured in cubic units.
See example on your book page 293.

26. Find the volume of the sphere below. Then show your
solution on the board.

27. Find the volume of the following problem. Read and
understand.
A spherical tank for natural gas has a
radius of 7 meters. About how many
cubic meters of natural gas can it hold?

28. Find the volume of the sphere.
8m
6m 10m

29. Solves routine and non-routine
problems involving volumes of
cylinder, cone and sphere.
What is the formula in to find the
volume of a:
1.Cylinder
2. Cone
3.Sphere

30. Arrange the following steps in solving the problem:
__4__A.What operation is needed to solve the
problem?
__2_B.What are the given facts?
__3_C.What is the correct number sentence?
__5_D.Write the solution with correct label.
_1__E.What is being asked?

31. Read and Understand.
Quezon City – an electric post, 150 cm long with
radius 15 cm, was hit by a truck yesterday at 4:30
a.m. This caused a two-hour brownout in the area.
The driver, Mr. Luis Mercado, and his friend, Mr.
Mark Fernando, were rushed to the nearby
hospital. Luckily, they just had mild contusions and
minor bruises. The two were being questioned as

32. Let us answer:
Find the volume of the
electric post, 150 cm long
with radius15 cm, that
was hit by a truck.

33. Solve the ff. problems:
1)A cone hat has a radius of 1.2 dm and a height of 3.4
dm. What is its volume?
2)Harold is molding a cylindrical candle with a
diameter of 12 cm and a height of 18 cm. About how
much wax does Harold need to mold the candle?
3.) A volleyball has a radius of 5.2 decimeters. What is
its volume? Use 3.14 for π.

34. Read and Understand:
Emilio and Jose pitched a tent that has
a shape of a pyramid. The base of the
tent is a rectangle that is 2.5 meters
wide and 2.8 meters long. The tent is 2
meters high. What is the volume of the
tent?

35. Group Activity:
Victor and Carlos are brothers. They share their
toys with each other. One day, they were
playing with dominoes. They were making
different shapes and figures out of these
dominoes. Victor made a rectangular solid
using 7 dominoes. If each domino has a length
of 3.5 cm, width of 2 cm, and a height of 1 cm,
find the volume of the rectangular figure that
Victor made.

36. Read and analyze each problem using 4-step
plan in solving the problem.
1.The base of a pyramid is 15 cm by 21
cm. Its height is 28 cm. Compute the
volume.
2. How many cubic meters of palay
can be placed in a box that is 45 m
long, 8 m wide and 7 m high?

37. Evaluation: Solve the following problems.
1.A rectangular water tank is meter wide, 1 meter long and
meters high. If it is half-filled, how much water does it
contain?
2.A box of milk is 9 cm long, 8 cm wide, and 18 cm high.
Find its volume.
3.The base of a pyramidal tent is a square. If the tent is 2
meters long and meters high, how many cubic meters of
space can it hold inside?
4. Alice has a paperweight in the shape of a pyramid. Its
height is 6 cm, length is 5.2 cm and width is 4.9 cm. What is

38. What is the formula in
finding the volumes of:

39. Who among you
encountered problems
in life?
What did you do to
solve that problem?

41. Step 1.Understand
a. What is asked?
b. What are the given facts?
Step 2.Plan
a. Which formula to use to solve
the problem?

42. Step 3. Solve
Show your computation
Step 4. Check
Go back to your computation.
Check the unit, and the given are
properly substituted with the
formula.

43. Practice Exercise:
1.Find the volume of an ice
cream cone that has radius of
2cm and a height of 5cm.
What is the volume of the ice
cream cone?

44. How do you solve word
problems involving volume
of the cone?
What are the steps in
solving routine and non-
routine problems?

45. Solve the following problems. Use the 4-step plan.
(1/2 crosswise)
1.The ice cream cone with a radius of
5.6 cm and a height of 1.3 cm.
Calculate the volume of the cone.
2.A cone has a height of 12 cm and the
radius is 7 cm. Calculate the volume of
the cone.

46. Read and Understand the
problem :
Emilio and Jose pitched a tent that
has a shape of a pyramid. The
base of the tent is a rectangle that
is 2.5 meters wide and 2.8 meters
long. The tent is 2 meters high.
What is the volume of the tent?

47. Group Activity: 3 Groups (Present your answer on the
board)
Read and understand the problem:
Victor and Carlos are brothers. They share their
toys with each other. One day, they were playing
with dominoes. They were making different
shapes and figures out of these dominoes. Victor
made a rectangular solid using 7 dominoes. If
each domino has a length of 3.5 cm, width of 2 cm,
and a height of 1 cm, find the volume of the

49. How do you solve
word problems
involving
measurement of
volume?

50. Solve the following problems. (1 whole sheet of paper)
1.A rectangular water tank is 6 meter wide,
8 meter long and 3 meters high. If it is half-
filled, how much water does it contain?
2.A box of milk is 9 cm long, 8 cm wide, and
18 cm high. Find its volume.
3.The base of a pyramidal tent is a square. If
the tent is 2 meters long and meters high,
how many cubic meters of space can it hold
inside?

51. Give me a number that is
a)one more than 9
b)one more than 99
c)one more than 999
What happens to 9 when you add 1?
What are the steps in solving a problem?

52. What are the electrical appliances
that you have at home?
How much do you pay for your
monthly electric bill?
How would you help lessen your electric
consumption? Why?

53. Mr. Dela Cruz is computing his monthly
electrical consumption. Based on his
electric bill, last month he was able to
consume 00125 kWh. When he checked his
digital electric meter, the reading is 00199
kWh. How many kilowatt-hours did Mr. Dela
Cruz consume this month?
Observe the meter readings on your book
page 302.

54. Assignment:
1. Read your electric meter.
2. Bring an old electric bill.

55. Read and interpret the dials on the electric meter
below.
73256kWh

56. Read and interpret the dials on the electric meter
below.

61. Read and Understand:
Ayie made a record of thier3-month
electric consumption. The initial reading is
973kWh.
January: 1120 kWh , February 1353 kWh
and March is 1512 kWh

62. a. How much will Ayie pay for
each month?
b. In what month did he pay the
most? the least?
c. What is the average monthly
consumption?

63. Practice Exercise: Read and Understand:
Mr. Reyes made a record of their 3-month
electric consumption. The initial reading is
876kWh.
March: 1320 kWh , April: 2353 kWh and
March is 6512 kWh
Assume that the basic charge for 5 pesos.

64. What is volume?

65. In math, volume is the amount of space
in a certain 3D object. For instance, a
fish tank has 3 feet in length, 1 foot in
width and two feet in height. To find the
volume, you multiply length times
width times height, which is 3x1x2,
which equals six. So the volume of the
fish tank is 6 cubic feet. Volume is also
how loud a sound is. Look on your TV
remote. There is a volume control

66. Aldrin has a part time job of the Body Fit Gym. His
boss wants to know the ages of the teenagers in the
center’s taekwondo class. Aldrin records the ages of
everyone in the class. Below are the ages of the
teenagers.
14 15 18 16 13 15 16 17 16
15 18 17 14 16 13 16 17 19

67. Data is the pieces of collected information. Using a
frequency table helps us to record , clarify and easily find
what we are looking for our data. In a tally table, a tally
marks are used to record data while frequency tables ,
numbers are used.
One of the first step to gather data is to arrange the
numbers in ascending or descending order so we can easily
see the highest and the lowest values.

68. Example 2:Pair Activity:
Mr. Guce , a grade 6 English teacher asked his 12
pupils about their weekly allowance. Make a
frequency table of the following data he collected.
How many pupils have an allowance of at least 250
pesos?
300.00 250.00 225.00 350.00
500.00 80.00 320.00 275.00
50.00 75.00 400.00 180.00

69. Pair Activity:
Ask your classmates favorite
subjects then make a frequency
table about their favorite subject.

71. What is a pie graph?
A pie graph is also known as
pie chart. The whole circle
represent one whole or 100%.

72. Paulo’s monthly allocation given as allowance of
P1, 200.

73. 1.How much is allotted per month for food
2.How much is spent for transportation?
3.How much does Paulo save in a month?
4.Find the average amount of money allotted per
month on food and transportation?
5.What is the average amount of money allotted
for school supplies, savings and miscellaneous
expenses?

76. ytilibaborp
probability

77. Probability is used to describe how
likely or unlikely it is that something
will happen. Probability may be given
in fraction, decimal or percent. The
value of probability ranges from 0-1 (0
means the event is impossible to
happen while 1 means the event is
certain to happen).

80. Which of the following situations can be
considered as unlikely to happen, likely to
happen, equally likely to happen, impossible to
happen, or certain to happen?
______1. The sun sets in the east.
_____ 2. A pregnant woman with a big and
round stomach may have a baby girl.
______ 3. An earthquake occurred. There will be
a tsunami.
______ 4. The teacher is beautiful, so she is a
very good teacher.
______ 5. The jeepney that runs is likely to meet
an accident.

81. Read each statement. Match it to the correct
prediction.
1. Billy was cold
2. The sun came out.
3. It started to rain.
4. The phone rang.
5. Mother is cooking.
a. We put on sunglasses.
b. Soon we will eat.
c. He put on a jacket.
d. I need an umbrella.

82. Directions: Which of the following situations can be
considered as unlikely to happen, likely to happen,
impossible to happen, or certain to happen?
1. Mark is thrifty. He will be rich someday.
2. When a pupil is absent, he is sick.
3. People living in the slum areas are poor.
4. When the teacher is out, the class is noisy.
5. Students prefer to have holidays than school
days.
6. Whales live in water, so they are classified as
fish.
7. The sun is the biggest star.
8. When a pupil cleans the room, a visitor is
coming.
9. A frog can live both on land and in water.

83. What can you see in the picture?
What will most
likely happen next?

84. Read each situation and tell what
will happen next.
1. Brendon woke up excited and
happy. The sun is shining. It was
perfect day for a trip to the beach.
2. Maggie knew that a storm was
coming. The sky was gray. A strong
wind began to blow. Thunder

85. Tell whether each situation can be
considered as:
- Likely to happen
- Certainly, to happen
- Unlikely to happen
- Impossible to happen
1. When a baby cries, he his hungry.
2. When a man is sad, he has no money.
3. Sneezing indicates that one has colds.
4. By experimenting, new things are
discovered.

86. Predict what will happen:
1. She is playing in the rain…
2. He is watching television at
night and not doing his
assignment…
3. The pupils are not listening…

87. Read the following situations and tell
which of them would be:
- - likely
- unlikely
1. If today is Friday, tomorrow will be
Saturday
2. Nicole will be in Puerto Princesa City in
less than an hour traveling by van.
3.The moon shines at noon today.
4. I suffer from indigestion. I will have a
soft diet for lunch.

88. Rolling a die, what is the probability that 9 come
out?
Activity 1:
You select a marble without looking and then put it
back. If you do this 8 times, what is the best prediction
possible for the number of times you will pick a marble
that is not blue?

89. Study the illustration below then answer the following questions
that follow.
THE CHIPS ARE PLACED IN A JAR AND MIXED
1. What is the probability of picking a chip with an even
number?
2. What is the probability of picking a chip with an odd number?
3. What is the probability of picking a chip with the biggest
number?
4. What is the probability of picking a chip with the smallest
number?
5. What is the probability of picking a chip with a prime
number?