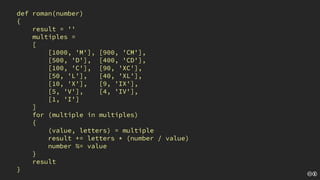
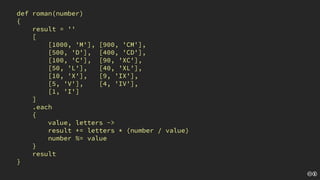
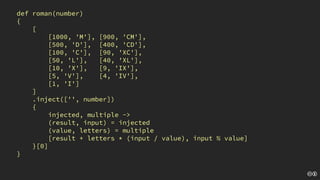
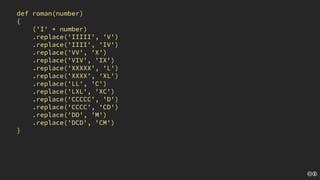
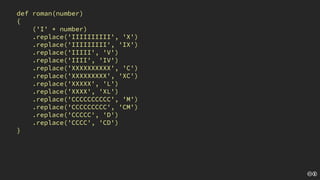
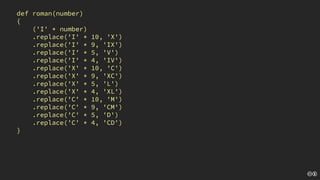
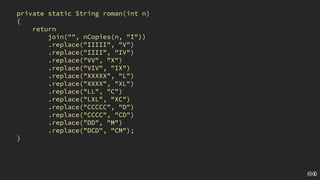
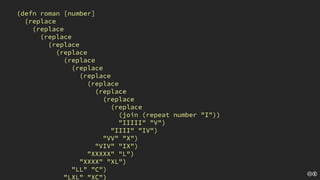
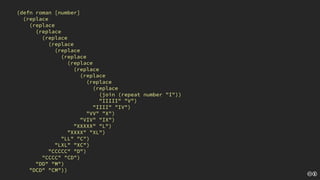
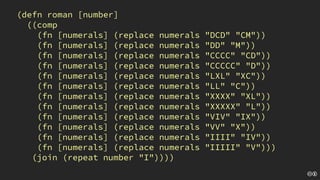
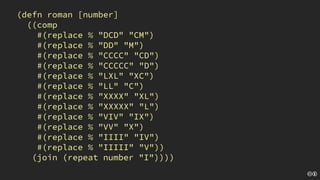
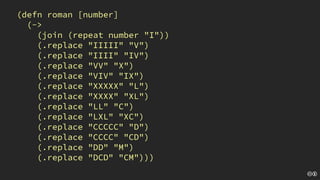
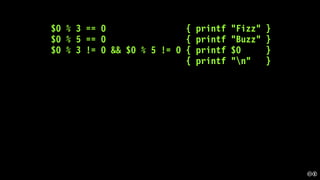
The document discusses the concept of deliberate practice for skill improvement, emphasizing its focus on mastery through repetition. It also explains the game of Fizz Buzz, which helps teach division and is used in programming interviews, outlining its rules and various coding implementations. Additionally, it touches on test-driven development principles through coding practices related to Fizz Buzz.























![Adults may play Fizz buzz as a
drinking game, where making
a mistake leads to the player
having to make a drinking-
related forfeit.
http://en.wikipedia.org/wiki/Fizz_buzz
[citation needed]](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-37-320.jpg)


















![fizzes = [''] + ([''] * 2 + ['Fizz']) * 33 + ['']
buzzes = [''] + ([''] * 4 + ['Buzz']) * 20
numbers = (0..100)*.toString()
def fizzbuzz(n)
{
fizzes[n] + buzzes[n] ?: numbers[n]
}](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-58-320.jpg)
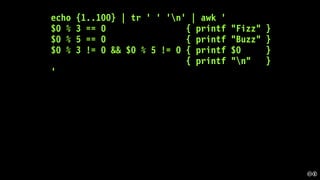
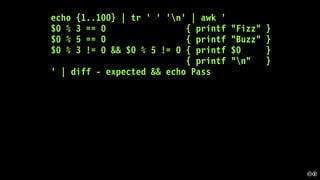
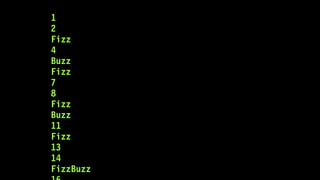
![We instituted a rigorous regression
test for all of the features of AWK. Any
of the three of us who put in a new
feature into the language [...], first
had to write a test for the new feature.
Alfred Aho
http://www.computerworld.com.au/article/216844/a-z_programming_languages_awk/](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-63-320.jpg)









![def fizzbuzz(n):
return {
1: lambda: '1',
2: lambda: '2',
3: lambda: 'Fizz',
4: lambda: '4',
5: lambda: 'Buzz',
6: lambda: 'Fizz',
7: lambda: '7',
8: lambda: '8',
9: lambda: 'Fizz',
10: lambda: 'Buzz',
11: lambda: '11',
12: lambda: 'Fizz',
13: lambda: '13',
14: lambda: '14',
15: lambda: 'FizzBuzz',
...
98: lambda: '98',
99: lambda: 'Fizz',
100: lambda: 'Buzz'
}[n]()](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-73-320.jpg)
![def fizzbuzz(n):
return {
1: '1',
2: '2',
3: 'Fizz',
4: '4',
5: 'Buzz',
6: 'Fizz',
7: '7',
8: '8',
9: 'Fizz',
10: 'Buzz',
11: '11',
12: 'Fizz',
13: '13',
14: '14',
15: 'FizzBuzz',
...
98: '98',
99: 'Fizz',
100: 'Buzz'
}[n]](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-74-320.jpg)
![def fizzbuzz(n):
return [
'1',
'2',
'Fizz',
'4',
'Buzz',
'Fizz',
'7',
'8',
'Fizz',
'Buzz',
'11',
'Fizz',
'13',
'14',
'FizzBuzz',
...
'98',
'Fizz',
'Buzz'
][n-1]](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-75-320.jpg)


![actual = [fizzbuzz(n) for n in range(1, 101)]
truths = [
every result is 'Fizz', 'Buzz', 'FizzBuzz' or a decimal string,
every decimal result corresponds to its ordinal position,
every third result contains 'Fizz',
every fifth result contains 'Buzz',
every fifteenth result is 'FizzBuzz',
the ordinal position of every 'Fizz' result is divisible by 3,
the ordinal position of every 'Buzz' result is divisible by 5,
the ordinal position of every 'FizzBuzz' result is divisible by 15
]
assert all(truths)](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-79-320.jpg)
![actual = [fizzbuzz(n) for n in range(1, 101)]
truths = [
all(a in {'Fizz', 'Buzz', 'FizzBuzz'} or a.isdecimal() for a in actual),
all(int(a) == n for n, a in enumerate(actual, 1) if a.isdecimal()),
all('Fizz' in a for a in actual[2::3]),
all('Buzz' in a for a in actual[4::5]),
all(a == 'FizzBuzz' for a in actual[14::15]),
all(n % 3 == 0 for n, a in enumerate(actual, 1) if a == 'Fizz'),
all(n % 5 == 0 for n, a in enumerate(actual, 1) if a == 'Buzz'),
all(n % 15 == 0 for n, a in enumerate(actual, 1) if a == 'FizzBuzz')
]
assert all(truths)](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-80-320.jpg)










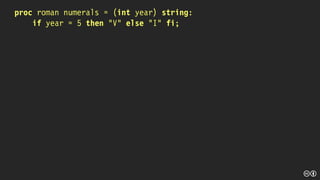
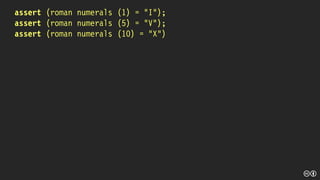
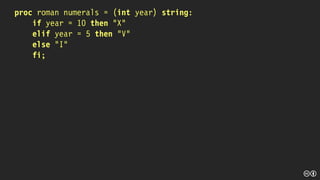
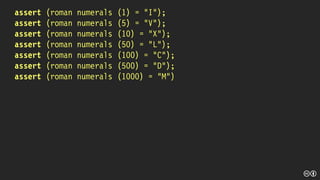
![[] struct (int value, string letters) mapping =
(
(1000, “M”),
(500, “D”),
(100, “C”),
(50, “L”),
(10, “X”),
(5, “V”),
(1, “I”)
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-104-320.jpg)
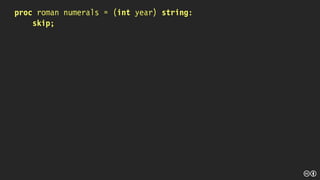
![proc roman numerals = (int year) string:
begin
string result := "";
for entry from lwb mapping to upb mapping do
if value of mapping[entry] = year then
result := letters of mapping[entry]
fi
od;
result
end;](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-105-320.jpg)
![proc roman numerals = (int year) string:
(
string result := "";
for entry from lwb mapping to upb mapping do
if value of mapping[entry] = year then
result := letters of mapping[entry]
fi
od;
result
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-106-320.jpg)
![[] proposition roman numerals spec =
(
("Decimal positions correspond to numerals",
((1, "I"), (10, "X"), (100, "C"), (1000, "M"))),
("Quinary values correspond to numerals",
((5, "V"), (50, "L"), (500, "D")))
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-107-320.jpg)

![[] proposition roman numerals spec =
(
("Decimal positions correspond to numerals",
((1, "I"), (10, "X"), (100, "C"), (1000, "M"))),
("Quinary intervals correspond to numerals",
((5, "V"), (50, "L"), (500, "D")))
);
test (roman numerals, roman numerals spec)](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-109-320.jpg)
![mode test = struct (int input, string expected);
mode proposition = struct (string name, flex [1:0] test tests);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-110-320.jpg)
![proc test = (proc (int) string function, [] proposition spec) void:
for entry from lwb spec to upb spec do
print (name of spec[entry]);
string report := "", separator := " failed:";
[] test tests = tests of spec[entry];
for test from lwb tests to upb tests do
int input = input of tests[test];
string expected = expected of tests[test];
string actual = function (input);
if actual /= expected then
report +:=
separator + " for " + whole (input, 0) +
" expected " + expected + " but was " + actual
separator := “,”
fi
od;
print (if report = "" then (new line) else (new line, report, new line) fi)
od;](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-111-320.jpg)
![[] proposition roman numerals spec =
(
("Decimal positions correspond to numerals",
((1, "I"), (10, "X"), (100, "C"), (1000, "M"))),
("Quinary intervals correspond to numerals",
((5, "V"), (50, "L"), (500, "D"))),
("Multiples of decimals are additive",
((2, "II"), (30, "XXX"), (200, "CC"), (4000, "MMMM")))
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-112-320.jpg)
![proc roman numerals = (int year) string:
(
string result := "";
int value = year;
for entry from lwb mapping to upb mapping do
if value mod value of mapping[entry] = 0 then
while value > 0 do
result +:= letters of mapping[entry];
value -:= value of mapping[entry]
od
fi
od;
result
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-113-320.jpg)
![[] proposition roman numerals spec =
(
("Decimal positions correspond to numerals",
((1, "I"), (10, "X"), (100, "C"), (1000, "M"))),
("Quinary intervals correspond to numerals",
((5, "V"), (50, "L"), (500, "D"))),
("Multiples of decimals are additive",
((2, "II"), (30, "XXX"), (200, "CC"), (4000, "MMMM"))),
("Non-multiples of decimals are additive",
((6, "VI"), (23, "XXIII"), (273, "CCLXXIII"), (1500, "MD")))
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-114-320.jpg)
![proc roman numerals = (int year) string:
(
string result := "";
int value = year;
for entry from lwb mapping to upb mapping do
while value >= value of mapping[entry] do
result +:= letters of mapping[entry];
value -:= value of mapping[entry]
od
od;
result
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-115-320.jpg)
![[] proposition roman numerals spec =
(
("Decimal positions correspond to numerals",
((1, "I"), (10, "X"), (100, "C"), (1000, "M"))),
("Quinary intervals correspond to numerals",
((5, "V"), (50, "L"), (500, "D"))),
("Multiples of decimals are additive",
((2, "II"), (30, "XXX"), (200, "CC"), (4000, "MMMM"))),
("Non-multiples of decimals are additive",
((6, "VI"), (23, "XXIII"), (273, "CCLXXIII"), (1500, "MD"))),
("Numeral predecessors are subtractive",
((4, "IV"), (9, "IX"), (40, "XL"), (90, "XC"), (400, "CD"), (900, "CM")))
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-116-320.jpg)
![[] struct (int value, string letters) mapping =
(
(1000, "M"), (900, "CM"),
(500, "D"), (400, "CD"),
(100, "C"), (90, "XC"),
(50, "L"), (40, "XL"),
(10, "X"), (9, "IX"),
(5, "V"), (4, "IV"),
(1, "I")
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-117-320.jpg)
![[] proposition roman numerals spec =
(
("Decimal positions correspond to numerals",
((1, "I"), (10, "X"), (100, "C"), (1000, "M"))),
("Quinary intervals correspond to numerals",
((5, "V"), (50, "L"), (500, "D"))),
("Multiples of decimals are additive",
((2, "II"), (30, "XXX"), (200, "CC"), (4000, "MMMM"))),
("Non-multiples of decimals are additive",
((6, "VI"), (23, "XXIII"), (273, "CCLXXIII"), (1500, "MD"))),
("Numeral predecessors are subtractive",
((4, "IV"), (9, "IX"), (40, "XL"), (90, "XC"), (400, "CD"), (900, "CM"))),
("Subtractive predecessors are additive",
((14, "XIV"), (42, "XLII"), (1968, "MCMLXVIII")))
);](https://image.slidesharecdn.com/getkata-190322074624/85/Get-Kata-118-320.jpg)