The document discusses key principles of functional programming, emphasizing its paradigm that focuses on treating computation as mathematical function evaluation, using pure functions, higher-order functions, and avoiding mutable state. It contrasts functional programming with other paradigms and provides examples in Python and Haskell to illustrate concepts. Additional references and reading materials related to functional programming are also mentioned.

1. A Few Function Programing Principles Every
Engineer Should Know
Jiaming Zhang
03/01/2017

2. Agenda
Scope
What's Functional Programing?
Functional Programing Principles
Reference/Reading

3. Scope
These won't be covered in this section (but already on my radar!)
FP Language
FP Design Pattern
FP Data Structures
FP w/ OOP
Success Stories

4. What's Functional Programing?
In computer science, functional programming is a programming
paradigm that treats computation as the evaluation of mathematical
functions and avoids changing-state and mutable data. [1]
[1] Wikipedia - Functional Programining

5. What's Functional Programing?
What's programing paradigm?
A style of building the structure and elements of computer programs.
Common paradiagm includes [1]:
Imperative
Declarative
Object-oriented
Functional
Note: Paradigm can overlap or can be used w/ each other.
[1] Definition of Programing Paradigms

6. FP Principles
Treat computation as the evaluation of math functions
Pure Function
High-order Function (or Functor)
Avoid Mutation
...

7. FP Principles
Treat computation as the
evaluation of math functions
A math function maps a set of input to a set of output.

8. FP Principles
Treat computation as the
evaluation of math functions
FP usually prefers expression over statement
# Assume val is int
# Statement
def abs1(val):
if val < 0:
return -val
else:
return val
# Expression
def abs2(val):
return -val if val < 0 else val

9. FP Principles
Treat computation as the
evaluation of math functions
An equivalent Haskell example

10. FP Principles
Treat computation as the
evaluation of math functions
An equivalent Haskell example
abs :: Int -> Int
abs val
| val < 0 = -val
| otherwise = val

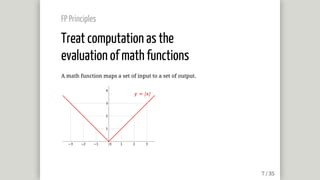
11. FP Principles
Treat computation as the
evaluation of math functions
FP usually prefers recursion over iteration
# Iteration - Procedural Style
def sum1(nums):
total = 0
for num in nums:
total += num
return total
# Recursion - Functional Style
def sum2(nums):
# Not very efficient in Python but you got the idea
return 0 if len(nums) == 0 else nums[0] + sum2(nums[1:])

12. FP Principles
Treat computation as the
evaluation of math functions
An equivalent Haskell example
sum :: [Int] -> Int
sum nums = case nums of
[] -> 0
x:xs -> x + sum2 xs

13. FP Principles
Pure Function
1. No side effect
2. Same input, same output

14. FP Principles
Pure Function
#1 No side effect
Example of Function w/ Site Effect

15. FP Principles
Pure Function
#1 No side effect
Example of Function w/ Site Effect
def sayhi(name)
print("Hi there, my name is %s" % name)
def write_to_file(file, text):
with open(file, 'w+') as f:
f.write(text)
def sort_nums(nums):
nums.sort() # inplace sort
return nums

16. FP Principles
Pure Function
#1 No side effect
But why create an app that can't change the "world"?

17. FP Principles
Pure Function
#1 No side effect
But why create an app that can't change the "world"?
In practice, applications need to have some side effects. Simon
Peyton-Jones, a major contributor to the functional programming
language Haskell, said the following: "In the end, any program must
manipulate state. A program that has no side effects whatsoever is a
kind of black box. All you can tell is that the box gets hotter." The key
is to limit side effects, clearly identify them, and avoid scattering
them throughout the code. [1]
[1] Why are side-effects considered evil in functional programming?

18. FP Principles
Pure Function
#2 Same input, same output
Example of Function that Violates this

19. FP Principles
Pure Function
#2 Same input, same output
Example of Function that Violates this
gloabl_counter = 0
function foo(x){
gloabl_counter += 1;
return gloabl_counter + x;
}
foo(1) // => 2
foo(1) // => 3

20. FP Principles
Pure Function
#2 Same input, same output
Example of Function that Violates this
gloabl_counter = 0
function foo(x){
gloabl_counter += 1;
return gloabl_counter + x;
}
foo(1) // => 2
foo(1) // => 3
Other examples?

21. FP Principles
High-order Function (or Functor)
1. Take at least one function as input or
2. Return a function

22. FP Principles
High-order Function (or Functor)
Example: A function that takes another function as input
nums = [1,2,3]
map(lambda x: x*2, nums)
# => [2,4,6]
filter(lambda x: x % 2 == 0, nums)
# => [2]
reduce(lambda total, num: total * num, nums)
# => 6

23. FP Principles
High-order Function (or Functor)
Example: A function that returns a function as output
dirs = ['lib', 'bin', 'log']
# `functools` is a built-in Python module
# `functools.partial` return a partial-applied func
func = functools.partial(os.path.join, '/User/jason')
map(func, dirs)
# => ['/User/jason/lib', '/User/jason/bin', '/User/jason/log']

24. FP Principles
High-order Function (or Functor)
Q: Can you do this w/ just lambda?

25. FP Principles
High-order Function (or Functor)
Q: Can you do this w/ just lambda?
map(lambda dirname: os.path.join('/User/jason', dirname), dirs)
# => ['/User/jason/lib', '/User/jason/bin', '/User/jason/log']

26. FP Principles
High-order Function (or Functor)
Another Example -- Compose
def compose(f, g):
def composed_func(val):
return g(f(val))
return composed_func

27. FP Principles
High-order Function (or Functor)
Another Example -- Compose
def compose(f, g):
def composed_func(val):
return g(f(val))
return composed_func
dirname = '~/lib/../log'
os.path.abspath(os.path.expanduser(dirname))
# => /Users/jiamingz/log
expandpath = compose(os.path.expanduser, os.path.abspath)
expandpath(dirname)
expandpath('~/lib/python/..')

28. FP Principles
High-order Function (or Functor)
Compose is a common high-order function in FP lang

29. FP Principles
High-order Function (or Functor)
Compose is a common high-order function in FP lang
add5 :: Int -> Int
add5 x = 5 + x
mul5 :: Int -> Int
mul5 x = 5 * x
mul5_and_add5 :: Int -> Int
mul5_and_add5 = add5 . mul5

30. FP Principles
Avoid Mutation
[1,2,3] -> [1,2,42]

31. FP Principles
Avoid Mutation
[1,2,3] -> [1,2,42]
Example: Mutation
def change(arr, idx, new_val):
arr[idx] = new_val
return arr

32. FP Principles
Avoid Mutation
[1,2,3] -> [1,2,42]
Example: Mutation
def change(arr, idx, new_val):
arr[idx] = new_val
return arr
Example: No Mutation
def change(arr, idx, new_val):
return arr[:idx] + [new_val] + arr[idx+1:]
change([1,2,3], 2, 42)
# => [1,2,42]

33. FP Principles
Avoid Mutation
Wait ... what about the efficiency?

34. FP Principles
Avoid Mutation
Wait ... what about the efficiency?
Persistent data structure
Not gonna cover to this time. If you're interested, check this Ideal Hash Tree

35. Reference/Reading
Wikipedia - Functional Programing
Wikipedia - Pure Function
Wikipedia - Higher Order Function
Anjana Vakil: Learning Functional Programming with JavaScript -
JSUnconf 2016
The Origins of Scala
Eassy - Why Functional Programing Matters by John Hughes
Youtube - Why Functional Programming Matters by John Hughes at
Functional Conf 2016