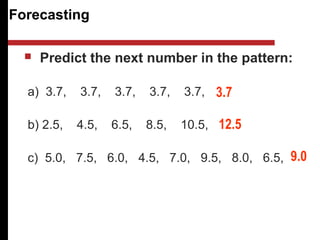
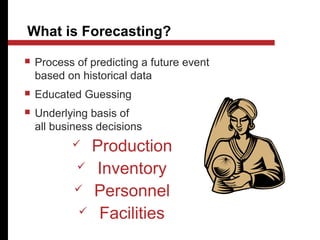
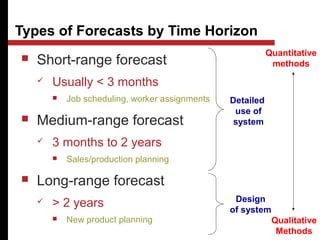
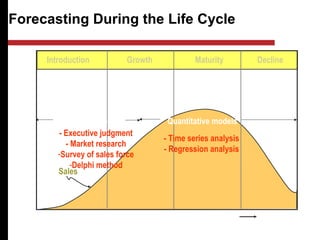
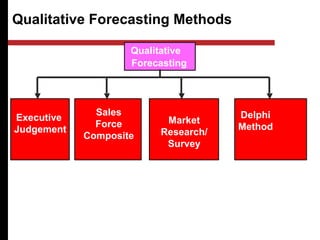
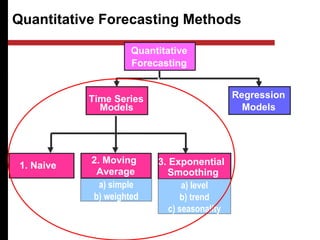
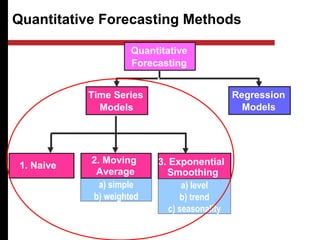
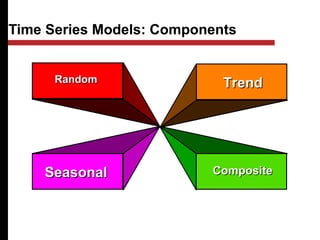
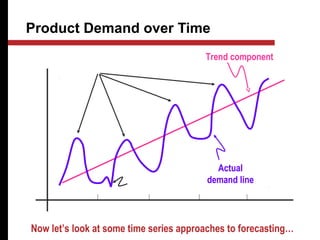
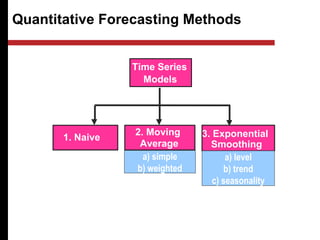
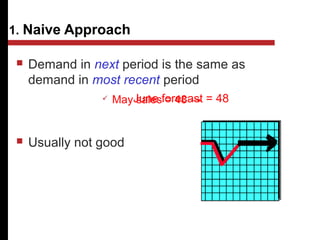
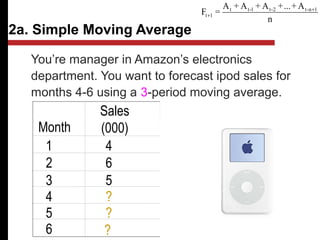
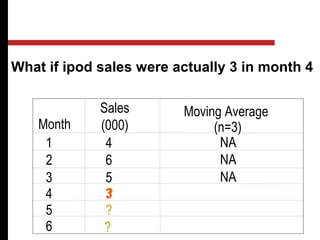
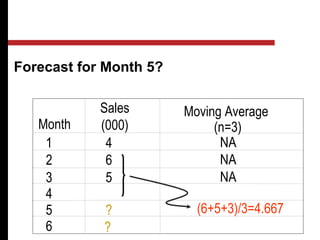
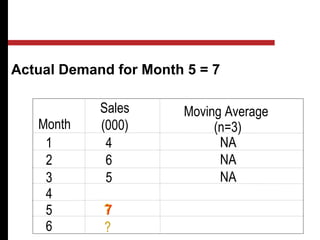
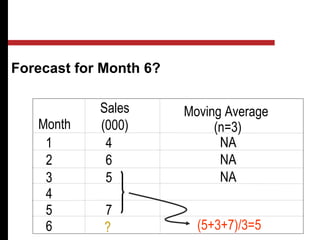
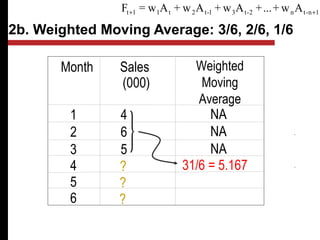
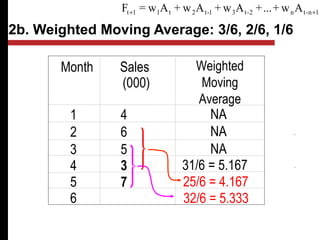
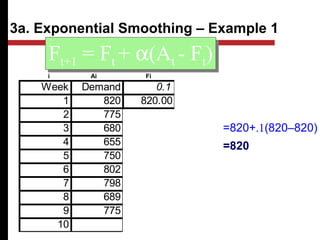
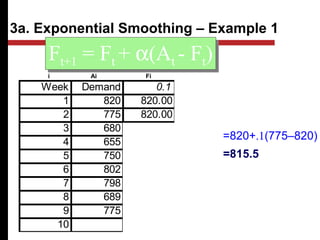
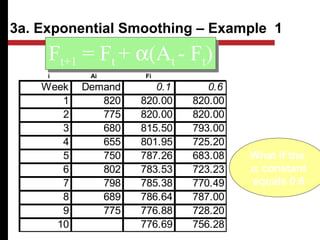
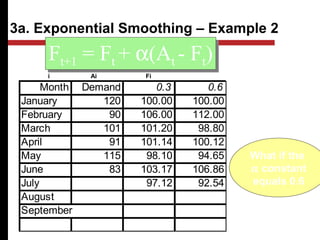
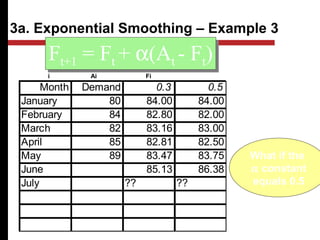
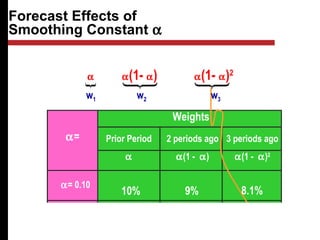
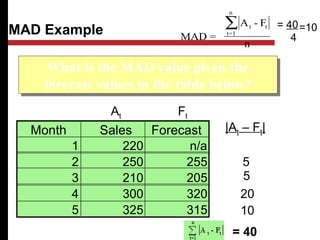
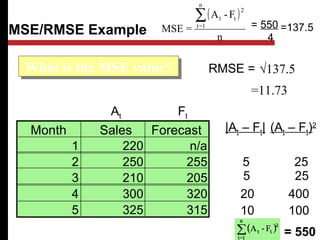
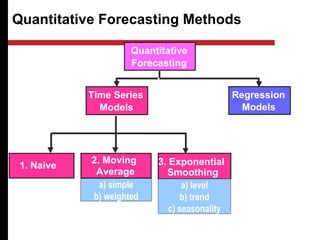
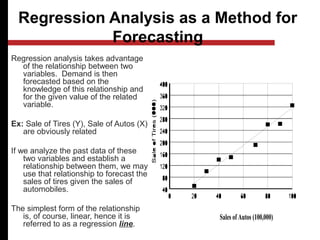
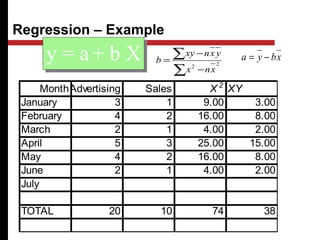
The document discusses various quantitative and qualitative forecasting methods. It begins by introducing forecasting and explaining its importance for business planning. It then outlines different types of forecasts based on time horizon (short, medium, long-range). The document proceeds to describe several quantitative time series forecasting models including naive, moving average (simple, weighted), and exponential smoothing (simple, with trend and seasonality components). It also briefly discusses qualitative methods such as executive judgment, sales force composite, market research, and the Delphi method. Examples are provided to illustrate exponential smoothing calculations.