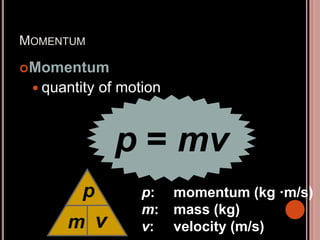
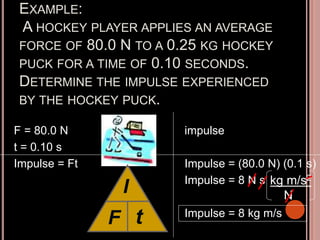
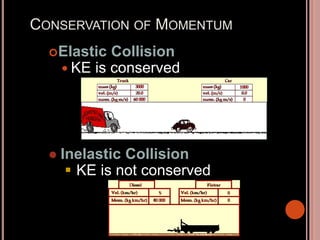
This document discusses Newton's three laws of motion. Newton's first law states that an object at rest stays at rest and an object in motion stays in motion unless acted upon by an external force. Newton's second law relates force, mass, and acceleration using the equation F=ma. Newton's third law states that for every action there is an equal and opposite reaction. The document also covers concepts such as inertia, momentum, impulse, and conservation of momentum.

1. CHAPTER 11 FORCE

2. NEWTON’S FIRST LAW
An object at rest will remain at rest and
an object in motion will continue in
motion at a constant velocity unless
acted upon by a net force

3. NEWTON’S FIRST LAW
Newton’s First Law of Motion
 “Law of Inertia”
Inertia
 tendency of an object to resist any
change in its motion
 increases as mass increases

4. INERTIA
 Inertia is the tendency to resist change in
motion
 Change in motion is always caused by a
force
 An object will keep doing what it’s doing
until a force acts on it

5. MASS AND INERTIA
 Massive objects resist change in motion
 Objects with more mass need larger forces to
change their motion

6. NEWTON’S 1ST LAW
 An object at rest (still) will
stay at rest until a force acts
on it.
 An object in motion will stay
in motion until a force acts
on it.

7. NEWTON’S 1ST LAW
 You aren’t wearing a seatbelt while driving
(NOT a good idea). You run your car into a
wall. Your car stops, but you remain in
motion, so you fly through the windshield.
 If you’re wearing your seatbelt, you slow
down with the car. Airbags can reduce the
force of the impact.

8. FORCE, MASS, AND ACCELERATION
Exerting a larger
force on an
object causes a
greater change
in velocity.
 A greater change in velocity means there is greater
acceleration.

9. NEWTON’S SECOND LAW
Newton’s Second Law of Motion
 The acceleration of an object is
directly proportional to the net force
acting on it and inversely
proportional to its mass.
 AKA-When mass goes up,
acceleration goes down, and when
force goes up, acceleration goes up
F = ma

10. FORCE, MASS, AND ACCELERATION
If the same force is exerted on a more
massive and a less massive object, the
more massive object can’t accelerate as
much.
The more massive object will have a
lower velocity.

11. NEWTON’S SECOND LAW
F = ma
F: force (N)
m: mass (kg)
a: accel (m/s2)
1 N = 1 kg ·m/s2

a
m
F
a
F
m

12. GRAVITY
Gravity
 force of attraction between any two
objects in the universe
 increases as...
mass increases (one or both
objects)
distance decreases

13. GRAVITY
Who experiences more gravity - the
astronaut or the politician?
less
distance
more
mass
 Which exerts more gravity -
the Earth or the moon?

14. GRAVITY
Weight
 the force of gravity on an object
MASS
always the same
(kg)
WEIGHT
depends on gravity
(N)
W = mg
W: weight (N)
m: mass (kg)
g: acceleration
due to gravity
(m/s2)

15. GRAVITY
Would you weigh more on Earth
or Jupiter?
greater gravity
greater weight
greater mass
 Jupiter because...

16. GRAVITY
Accel. due to gravity (g)
 In the absence of air
resistance, all falling objects
have the same acceleration!
 On Earth: g = 9.8 m/s2
m
W
g 
elephant
m
W
g 
feather
Animation from “Multimedia Physics Studios.”

17. CALCULATIONS
 What force would be required to
accelerate a 40 kg mass by 4 m/s2?
GIVEN:
F = ?
m = 40 kg
a = 4 m/s2
WORK:
F = ma
F = (40 kg)(4 m/s2)
F = 160 N
m
F
a

18. CALCULATIONS
 A 4.0 kg shotput is thrown with 30 N of
force. What is its acceleration?
GIVEN:
m = 4.0 kg
F = 30 N
a = ?
WORK:
a = F ÷ m
a = (30 N) ÷ (4.0 kg)
a = 7.5 m/s2
m
F
a

19. CALCULATIONS
 Mrs. Ellis weighs 572 N. What is her
mass?
GIVEN:
F(W) = 572 N
m = ?
a(g) = 9.8 m/s2
WORK:
m = F ÷ a
m = (572 N) ÷ (9.8 m/s2)
m = 58.4 kg
m
F
a

20. CONCEPTEST
Is the following statement true or false?
 An astronaut has less mass on the moon
since the moon exerts a weaker
gravitational force.
 False! Mass does not depend on
gravity, weight does. The astronaut has
less weight on the moon.

21. FREE-FALL
Free-Fall
 when an object is influenced only
by the force of gravity
Weightlessness
 sensation produced when an
object and its surroundings are in
free-fall
 object is not weightless!
CUP DEMO

22. FREE-FALL
Weightlessness
 surroundings are falling at the same
rate so they don’t exert a force on the
object

23. FREE-FALL
NASA’s KC-135 - “The Vomit Comet”
Go
to
NASA.
Go
to
CNN.com.
Go
to
Space
Settlement
Video
Library.
Space Shuttle Missions

24. CONCEPTEST 1
TRUE or FALSE:
An astronaut on the Space Shuttle
feels weightless because there is no
gravity in space.
FALSE!
There is gravity which is causing the
Shuttle to free-fall towards the Earth.
She feels weightless because she’s
free-falling at the same rate.

25. NEWTON’S THIRD LAW
 Newton’s Third Law of Motion
 When one object exerts a force on a second object, the
second object exerts an equal but opposite force on the
first.

26. NEWTON’S THIRD LAW
 One object exerts a force on the second object
 The second exerts a force back that is equal in
strength, but opposite in direction

27. NEWTON’S THIRD LAW
Problem:
 How can a horse
pull a cart if the cart
is pulling back on
the horse with an equal but
opposite force?
NO!!!
 Aren’t these “balanced forces”
resulting in no acceleration?

28. NEWTON’S THIRD LAW
 forces are equal and opposite but
act on different objects
 they are not “balanced forces”
 the movement of the horse
depends on the forces acting on
the horse
 Explanation:

29. NEWTON’S THIRD LAW
 Action and Reaction
forces do not cancel –
they can act on different
objects or spread in
different directions

30. NEWTON’S THIRD LAW
Action-Reaction Pairs
 The hammer exerts
a force on the nail
to the right.
 The nail exerts an
equal but opposite
force on the
hammer to the left.

31. NEWTON’S THIRD LAW
Action-Reaction Pairs
 The rocket exerts a
downward force on the
exhaust gases.
 The gases exert an
equal but opposite
upward force on the
rocket.
FG
FR

32. NEWTON’S THIRD LAW
Action-Reaction Pairs
 Both objects accelerate.
 The amount of acceleration
depends on the mass of the object.

a F
m
 Small mass  more acceleration
 Large mass  less acceleration

33. MOMENTUM
Momentum
 quantity of motion
p = mv
p: momentum (kg ·m/s)
m: mass (kg)
v: velocity (m/s)
m
p
v

34. MOMENTUM:
 inertia in motion
 when you’re moving,
momentum keeps you
moving
 an object with lots of
momentum is hard to stop

35. MOMENTUM:
 p = mv
 p = momentum (in kg m/s)
 m = mass (in kg)
 v = velocity (in m/s)
 momentum is a vector quantity, so a complete
answer will include magnitude and direction
m
p
v

36. IS IT POSSIBLE FOR A MOTORCYCLE AND
A LARGE TRUCK TO HAVE THE SAME
MOMENTUM?
m = 40,000 kg
m = 400 kg

37. MOMENTUM
 Find the momentum of a bumper car if it
has a total mass of 280 kg and a velocity
of 3.2 m/s.
GIVEN:
p = ?
m = 280 kg
v = 3.2 m/s
WORK:
p = mv
p = (280 kg)(3.2 m/s)
p = 896 kg·m/s
m
p
v

38. MOMENTUM
 The momentum of a second bumper car
is 675 kg·m/s. What is its velocity if its
total mass is 300 kg?
GIVEN:
p = 675 kg·m/s
m = 300 kg
v = ?
WORK:
v = p ÷ m
v = (675 kg·m/s)÷(300 kg)
v = 2.25 m/s
m
p
v

39. EXAMPLE:
WHAT IS THE MOMENTUM OF A 150 KG
DEFENSIVE TACKLE AT 5 M/S NORTH
TOWARDS THE END ZONE?

40. EXAMPLE:
WHAT IS THE MOMENTUM OF A 325
POUND DEFENSIVE TACKLE AT 5 M/S
NORTH TOWARDS THE END ZONE?
m = 150 kg)
v = 5 m/s north
p = mv
momentum
p = (150 kg) (5 m/s)
p = 750 kg m/s north

41. TO CHANGE THE MOMENTUM OF AN
OBJECT, YOU MUST CHANGE…
 mass and/or velocity
 usually velocity changes
 change in velocity is acceleration
 to make an object accelerate, a force is required
 So a force causes a change in the momentum of an
object.
 Size of force and the time the force acts both affect
change in momentum.

42. THE IMPORTANCE OF “FOLLOWING
THROUGH” IN SPORTS
 The follow-through
increases the time of
collision and thus
increases the change in
momentum, making the
ball have a higher
velocity!

43. IMPULSE:
 what changes the momentum
 Depends on force and time of collision
 Impulse = Ft
 Impulse = change of momentum
 units for impulse are same as units for momentum
 Impulse = Δp
OR
 Ft = m(Δv)
F
I
t
m
I
Δv

44. EXAMPLE:
A HOCKEY PLAYER APPLIES AN AVERAGE
FORCE OF 80.0 N TO A 0.25 KG HOCKEY
PUCK FOR A TIME OF 0.10 SECONDS.
DETERMINE THE IMPULSE EXPERIENCED
BY THE HOCKEY PUCK.

45. EXAMPLE:
A HOCKEY PLAYER APPLIES AN AVERAGE
FORCE OF 80.0 N TO A 0.25 KG HOCKEY
PUCK FOR A TIME OF 0.10 SECONDS.
DETERMINE THE IMPULSE EXPERIENCED
BY THE HOCKEY PUCK.
F = 80.0 N
t = 0.10 s
Impulse = Ft
impulse
Impulse = (80.0 N) (0.1 s)
Impulse = 8 N s
Impulse = 8 kg m/s
kg m/s2
N
F
I
t

46. EXAMPLE #2
 What is the change in momentum (impulse) of a
950 kg car that travels from 40 m/s to 31 m/s?
GIVEN:
I = ?
m = 950 kg
Δv = 40-31 m/s
= 9 m/s
WORK:
I = m Δ v
I = (950 kg)(9m/s)
I = 8550 kg·m/s
m
I
Δv

47. EXAMPLE #3
 If the from the last problem had an impulse of 8550
kg*m/s, and it took 30 seconds to change speeds,
then what force caused the change?
GIVEN:
I = 8550 kg* m/s
F = ? N
t= 30 s
WORK:
F= I÷ t
F = (8550)÷ (30)
F = 285 N
F
I
t

48. THE EFFECT OF COLLISION TIME UPON THE
FORCE
Impulse (kg m/s) Time (s) Force (N)
100 1 100
100 2 50
100 4 25
100 10 10
100 25 4
100 50 2
100 100 1
100 1000 0.1
F
I
t

49. TIME AND FORCE ARE ________
PROPORTIONAL.
 For an object in a collision,
 to decrease the effect of the force, the time
must be increased
 To Increase the effect of the force, the time
must be decreased.
inversely

50. AIR BAGS
 Air bags increase the
time allowed to stop
the momentum of the
driver and passenger,
decreasing the force
of impact.
 Time increases 100
times!
 Force decreases
100 times!

51. USE OF MATS IN SPORTS
 Mats increase the time
allowed to stop the
momentum of the
athlete, decreasing the
force of impact.

52. “RIDING THE PUNCH”
 When a boxer recognizes
that he will be hit in the head
by his opponent, the boxer
often relaxes his neck and
allows his head to move
backwards upon impact.
 “Riding the punch” increases
the time the force is applied,
decreasing the force of
impact.

53. CONSERVATION OF MOMENTUM
Law of Conservation of Momentum
 The total momentum in a group of
objects doesn’t change unless
outside forces act on the objects.
pbefore = pafter

54. CONSERVATION OF MOMENTUM
Elastic Collision
 KE is conserved
 Inelastic Collision
 KE is not conserved

55. CONSERVATION OF MOMENTUM
 A 5-kg cart traveling at 1.2 m/s strikes a
stationary 2-kg cart and they connect.
Find their speed after the collision.
BEFORE
Cart 1:
m = 5 kg
v = 4.2 m/s
Cart 2 :
m = 2 kg
v = 0 m/s
AFTER
Cart 1 + 2:
m = 7 kg
v = ?
p = 21 kg·m/s
p = 0
pbefore = 21 kg·m/s pafter = 21 kg·m/s
m
p
v
v = p ÷ m
v = (21 kg·m/s) ÷ (7 kg)
v = 3 m/s

56. CONSERVATION OF MOMENTUM
 A 50-kg clown is shot out of a 250-kg
cannon at a speed of 20 m/s. What is
the recoil speed of the cannon?
BEFORE
Clown:
m = 50 kg
v = 0 m/s
Cannon:
m = 250 kg
v = 0 m/s
AFTER
Clown:
m = 50 kg
v = 20 m/s
Cannon:
m = 250 kg
v = ? m/s
p = 0
p = 0
pbefore = 0
p = 1000 kg·m/s
pafter = 0
p = -1000 kg·m/s

57. CONSERVATION OF MOMENTUM
 So…now we can solve for velocity.
GIVEN:
p = -1000 kg·m/s
m = 250 kg
v = ?
WORK:
v = p ÷ m
v = (-1000kg·m/s)÷(250kg)
v = - 4 m/s
(4 m/s backwards)
m
p
v