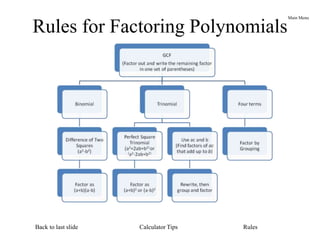
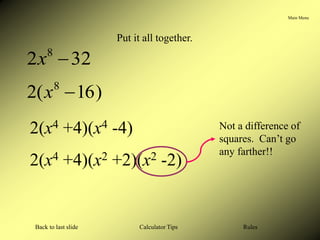This document provides step-by-step instructions for factoring polynomials. It begins with an overview of the general process, including checking for a greatest common factor, determining if the polynomial is binomial, trinomial, or four-term, and applying specific factoring patterns. The document then works through examples of factoring various polynomials like trinomials, differences of squares, and perfect square trinomials. It concludes with tips for using a calculator to find factors of the ac term when factoring trinomials.

1. Main Menu
Calculator Tips
Back to last slide Rules
Factoring Polynomials
A presentation for the
greatest Algebra I kids at RJR
By Mrs. Sexton

2. Main Menu
Calculator Tips
Back to last slide Rules
24
14
2

 x
x
Main Menu
Rules
Step by Step
Easy Problems Medium Problems
Hard Problems Word Problems
2
3
9
3 x
x 
16
4 2

s
p
py
m
my 15
3
20
4 


2
2
200
8 t
s 
6
5
6 2

 y
y
x
x
x 9
15
6 2
3


32
2 8

x
Division of polynomial by monomial
Find dimensions when area is given

3. Main Menu
Calculator Tips
Back to last slide Rules
Rules for Factoring Polynomials

4. Main Menu
Calculator Tips
Back to last slide Rules
Step by Step
• Is there a GCF?
– Yes
• Factor as the product of the GCF and one other factor—i.e.
GCF•(the other factor). Look at the other factor and go to the
next step below with it.
– No
• Go the the next step.
• Is it a binomial?
– Yes
• Is it a difference of two squares? (a2-b2)
– Yes—Factor as (a+b)(a-b).
– No—It can’t be factored any more.
– No
• Go to the next step.

5. Main Menu
Calculator Tips
Back to last slide Rules
• Is it a trinomial?
– Yes
• Do you recognize it as a pattern for a perfect square
trinomial? (a2+2ab+b2) or (a2-2ab+b2)
– Yes—Factor as (a+b)2 or (a-b)2
– No—Go to next step.
• Use the ac and b pattern to look for factors.
• Can you find factors of ac that add up to b?
– Yes—Rewrite the equation with those factors, group, and
factor.
– No—You can’t do anything else. If there’s no GCF, it’s a
prime polynomial.
– No
• Go to the next step.

6. Main Menu
Calculator Tips
Back to last slide Rules
• Is it a four-term polynomial?
– Yes
• Are there two sets of terms that you can group
together that have a common factor?
– Yes—Group and factor.
– No—If it doesn’t have a GCF, it’s a prime polynomial.
– No
• If it doesn’t have a GCF, it’s a prime polynomial.

7. Main Menu
Calculator Tips
Back to last slide Rules
NOTE:
At EVERY step along the way, you
must look at the factors that you get to
see if they can be factored any more.
Factoring completely means that no factors can be
broken down any further using any of the rules
you’ve learned.

8. Main Menu
Calculator Tips
Back to last slide Rules
Practice
24
14
2

 x
x
Factor completely.
Is there a GCF?
No. Is it a binomial, trinomial, or four-term polynomial?
It’s a trinomial.
Do you recognize it as a perfect square trinomial?
No. Use ac and b.

9. Main Menu
Calculator Tips
Back to last slide Rules
Use your handy-dandy calculator or
your super math skills to find 12
and 2 as the factors to use.
ac b
1 • 24 14
24
12, 2
Rewrite the equation with those two factors in the middle.
24
2
12
2


 x
x
x
24
14
2

 x
x
Group.
)
24
2
(
)
12
( 2


 x
x
x Factor out the GCF
from each group.
)
12
(
2
)
12
( 

 x
x
x Write the two factors.
)
2
)(
12
( 
 x
x Neither one of these factors can be
broken down any more, so you’re done.

10. Main Menu
Calculator Tips
Back to last slide Rules
2
3
9
3 x
x 
Factor completely
Is there a GCF?
Is it a binomial, trinomial, or four-term polynomial?
Yes. Write the GCF first and the remaining factor after it.
)
3
(
3 2

x
x Look at the remaining factor. (x-3)
It’s a binomial. Is it a difference of two squares? (a2-b2)
No. You can’t do anything else.
)
3
(
3 2

x
x is the completely factored form.

11. Main Menu
Calculator Tips
Back to last slide Rules
Factor completely
16
4 2

s Is there a GCF?
Yes. Write the GCF first and the remaining factor after it.
)
4
(
4 2

s Look at the remaining factor. (s2-4)
Is it a binomial, trinomial, or four-term polynomial?
It’s a binomial. Is it a difference of two squares? (a2-b2)
Yes. s2 is a square (s • s) and 4 is a square (2 • 2).
Factor as (s+2)(s-2). Then write the complete
factorization.
)
2
)(
2
(
4 
 s
s

12. Main Menu
Calculator Tips
Back to last slide Rules
Factor completely
p
py
m
my 15
3
20
4 

 Is there a GCF?
No. There is no single factor that goes into all four of the terms.
Is it a binomial, trinomial, or four-term polynomial?
It’s a four-term polynomial. Factor by grouping.
)
15
3
(
)
20
4
( p
py
m
my 

 Factor out the
GCF from each
group.
)
5
(
3
)
5
(
4 

 y
p
y
m
)
5
)(
3
4
( 
 y
p
m Write the two factors.

13. Main Menu
Calculator Tips
Back to last slide Rules
Factor completely
)
25
(
8 2
2
t
s 
Is there a GCF?
Yes. Write the GCF first and the remaining factor after it.
Look at the remaining factor. (s2-25t2)
Is it a binomial, trinomial, or four-term polynomial?
It’s a binomial. Is it a difference of two squares? (a2-b2)
Yes. s2 is a square (s • s) and 25t2 is a square (5t • 5t).
Factor as (s+5t)(s-5t). Then write the complete
factorization.
)
5
)(
5
(
8 t
s
t
s 

2
2
200
8 t
s 

14. Main Menu
Calculator Tips
Back to last slide Rules
Factor completely
6
5
6 2

 y
y Is there a GCF?
Is it a binomial, trinomial, or four-term polynomial?
No.
It’s a trinomial.
Do you recognize it as a perfect square trinomial?
No. Use ac and b.

15. Main Menu
Calculator Tips
Back to last slide Rules
ac b
6 • -6 -5
-36
4, -9
Look for factors of –36 that add up
to –5. Use your calculator or your
math skills to find 4 and -9 as the
factors to use.
Rewrite the equation with those two factors in the middle.
)
6
4
(
)
9
6
( 2


 y
y
y
6
5
6 2

 y
y
Group.
6
4
9
6 2


 y
y
y
Factor out the GCF
from each group.
)
3
2
(
2
)
3
2
(
3 

 y
y
y Write the two factors.
)
2
3
)(
3
2
( 
 y
y

16. Main Menu
Calculator Tips
Back to last slide Rules
x
x
x 9
15
6 2
3


Factor completely
Is there a GCF?
Yes. Write the GCF first and the remaining factor after it.
)
3
5
2
(
3 2

 x
x
x Look at the remaining factor.
)
3
5
2
( 2

 x
x
Is it a binomial, trinomial, or four-term polynomial?
It’s a trinomial.
Do you recognize it as a perfect square trinomial?
No. Use ac and b.

17. Main Menu
Calculator Tips
Back to last slide Rules
ac b
2 • -3 5
-6
6, -1
Look for factors of -6 that add up to
5. Use your calculator or your
math skills to find 6 and -1 as the
factors to use.
Rewrite the equation with those two factors in the middle.
Group. Remember to change the –3 to a
+3 because of the minus sign in the
grouping!!
Factor out the GCF
from each group.
Write all three factors.
)
3
5
2
(
3 2

 x
x
x
]
3
1
6
2
[
3 2


 x
x
x
x
)]
3
1
(
)
6
2
[(
3 2


 x
x
x
x
)]
3
(
1
)
3
(
2
[
3 

 x
x
x
x
)
1
2
)(
3
(
3 
 x
x
x

18. Main Menu
Calculator Tips
Back to last slide Rules
32
2 8

x
Factor completely
Is there a GCF?
Yes. Write the GCF first and the remaining factor after it.
)
16
(
2 8

x Look at the remaining factor.
)
16
( 8

x
Is it a binomial, trinomial, or four-term polynomial?
Yes. x8 is a square (x4 • x4) and 16 is a square
(4 • 4). Factor as (x4 + 4)(x4 - 4).
It’s a binomial. Is it a difference of two squares? (a2-b2)
So far we have 2(x4 + 4)(x4 - 4).
(Please continue—not done yet!!)

19. Main Menu
Calculator Tips
Back to last slide Rules
2(x4 +4)(x4 -4)
Look at what you have. Can either of the binomials be broken
down?
(x4 +4)
Is this binomial a difference of two squares? (a2-b2)
No. It can’t be broken down. So, we have to keep this factor.
(x4 -4)
Is this binomial a difference of two squares? (a2-b2)
Yes. x4 is a square (x2 • x2) and 4 is a square
(2 • 2). Factor as (x2 + 2)(x2 - 2).
What about the other binomial?

20. Main Menu
Calculator Tips
Back to last slide Rules
Put it all together.
32
2 8

x
)
16
(
2 8

x
2(x4 +4)(x4 -4)
2(x4 +4)(x2 +2)(x2 -2)
Not a difference of
squares. Can’t go
any farther!!

21. Main Menu
Calculator Tips
Back to last slide Rules
Word Problem #1
What is the quotient when
x
x
x 16
8
12 2
3

 is divided by 4x?
2
3x
This question is
asking you to find
the OTHER
FACTOR after you
take out the greatest
common factor of 4x.
Simplify each term.
x
x
x
x
x
x
x
x
x
x
4
16
4
8
4
12
4
16
8
12 2
3
2
3





x
2 4
 
4
2
3 2

 x
x

22. Main Menu
Calculator Tips
Back to last slide Rules
Word Problem #2
A rectangular garden plot has an area
represented by the expression
28
3
18 2

 x
x
Find the dimensions of the garden plot.
This is a factoring problem. You need to
find the two factors that multiply together
to give you 28
3
18 2

 x
x

23. Main Menu
Calculator Tips
Back to last slide Rules
Is there a GCF?
Is it a binomial, trinomial, or four-term polynomial?
No.
It’s a trinomial.
Do you recognize it as a perfect square trinomial?
No. Use ac and b.
28
3
18 2

 x
x

24. Main Menu
Calculator Tips
Back to last slide Rules
ac b
18 • -28 -3
-504
21, -24
Look for factors of –504 that add
up to –3. Use your calculator or
your math skills to find 21 and -24
as the factors to use.
Rewrite the equation with those two factors in the middle.
)
28
21
(
)
24
18
( 2


 x
x
x
Group.
28
21
24
18 2


 x
x
x
Factor out the GCF
from each group.
)
4
3
(
7
)
4
3
(
6 

 x
x
x Write the two factors.
)
7
6
)(
4
3
( 
 x
x
28
3
18 2

 x
x
Length is 3x - 4 and width is 6x + 7

25. Main Menu
Calculator Tips
Back to last slide Rules
Calculator Tips
To find factors of the ac term, use the following steps in your
calculator:
•Press the Y= button.
•In Y1=, type the ac value / X.
•In Y2=, type X + VARS, arrow to Y_VARS, Enter, Enter
•Go to Table and look for the b in column Y2. When you find it, use the
values in the X column and the Y1 column as your two factors to put in the
equation. IF YOU CAN’T find the b value in the Y2 column, the trinomial
can’t be factored.
•NOTE: Remember that you might need to scroll up the screen
to find negative numbers that give you the correct value in the Y2
column.