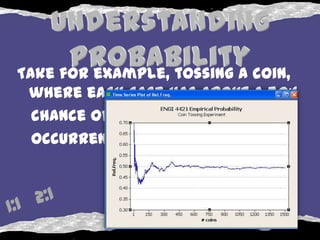
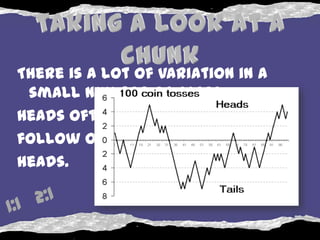
1) The document discusses probability and examples involving coin flips, dice rolls, and birthdays. 2) Probability is determined by considering all possible outcomes of an event, not any single outcome. Each individual event is independent. 3) The probability of two people sharing a birthday in a group increases as the number of people increases, reaching 50% once the group size reaches approximately 23 people.

2. ...that a flipped coin will turn up
heads
... that when you meet one
twin, she is the older one
Odds like 1:2 are depressing.
A 50% chance seems helpless
but sometimes, the odds aren’t

3. 1

4. 1

5. %#$&!!!
1

7. Initially, door #3 had 1:3
odds at being the winning
1
door and 2:3 odds at
being empty
However, when door #1
turned out to be empty,
door #3 still had 1:3
odds at being the winner
but door #2 had 2:3 odds

8. If only I
had taken
EDUC 211
Door Door Door
#1 #2 #3
1
Case  
1
Case  
2
Case  

9. WHAT: Probe meaning to "find out"
AND
“proof” means what is claimed to
be true.
WHERE: Probability originated from
the study of
games of chance and gambling
during the 16th century.
BY WHOM: Probability theory was a

11. • The last 10 times this penny has
been flipped, it has shown heads
• What is most probable to show
next? Heads, or Tails?
• Many people believe that
betting on Tails offers a higher
probability
Is this a Myth or are your

12. • Probability is long-term
outcome, is does not rely on
individual events.
• Each probabilistic event is an
isolated event, unaffected by
past or future events.
• Probability is the pattern of
infinitely many of such events.

13. Take for example, tossing a coin,
where each case has about a 50%
chance of
occurrence.

14. There is a lot of variation in a
small number of cases.
Heads often
follow other
heads.

15. It is only upon observing a
MASSIVE amount ofa cases that
Tossing Coin Infinite Times
probability
100
90
80
sketches 70 60
50
Itself out. 30
40
20
10
0
0 . . . . . . . . and
on

16. • A single event is uninfluenced by
past events
• Probability takes into account
ALL events
• When tossing a coin a single
time, it is either Heads or Tails
• The probability is 100% of either
or

17. Lesson?
Each event is isolated and
unaffected by other events
Even if a coin has shown heads the
Yes! past 10 times, the next toss has and
equal probability of showing heads
After flipping heads twenty
or tails. This can also be
demonstrated with the birth of
times, each event is still a single
children.
event.
A coin is not influenced by past or
future events.
Each individual event has equal
chance of showing heads or
tails, it is only over the long

18. Lets go back to the birthday
question:
How many people are needed
in a room so that the
probability that there are
at least two people whose
birthdays are the same day

19. Using the same format as the dice
questions earlier, we can easily
find the answer to this question.
• Remember that a way determine
the probability of something
happening is to subtract the
probability of something not
happening from 1 (or 100%).

20. A die has six sides.
Each roll will reveal one side.
The probability of any one
number showing is 1/6.
Let's say we have 2 dice, what is
the probability of having two
different numbers showing?
We can find the answer easier by

21. When we roll a pair of dice, there
are 36 (6 x 6) equally likely
outcomes.
The ones that have the same number
are 1 and 1, 2 and 2, 3 and 3, 4 and
4, 5 and 5, and 6 and 6 (6/36).
Instead of listing all the possible
outcomes, we can go 1 (100%)
subtract 6/36 (the probability of

22. The probability of an event
occurring E can be represented
by the equation: 1 – probability
of E not occurring.
So the birthday question has the
same format.
• Please turn to page 594.

23. Let's try to find the probability of
two people share the same
birthday.
We can begin by finding the answer of
the opposite question: the
probability that two people do not
share the same birthday.
365 possible birthdays for the first
person
364 possible birthdays for the second

24. So using what we learned previously
from the dice question:
For two people to have the same
birthday, the probability will
equal to
How many people are needed, then, so
that we can find a probability of
roughly one-half for two people

25. So if we had kept going with that
pattern...
Number of people Probability that at least two
in the room people share a birthday
5 0.027...
10 0.116...
15 0.252...
20 0.411...
25 0.568...
30 0.706
... ...