Embed presentation
Download to read offline


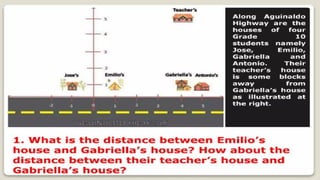
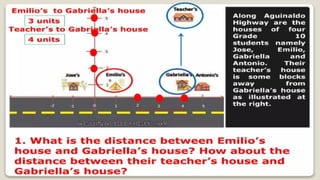
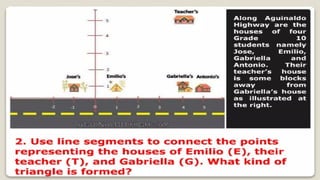
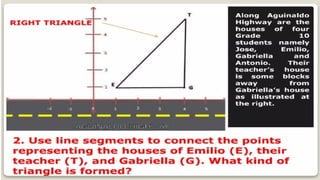
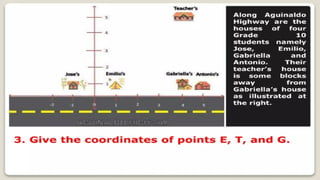
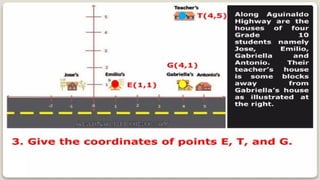
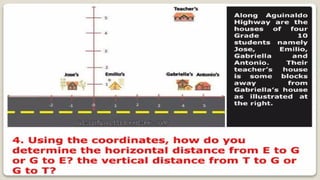
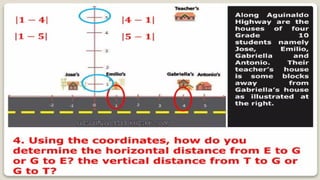


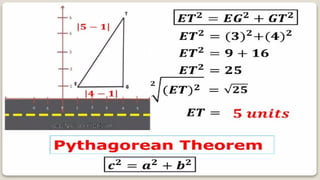


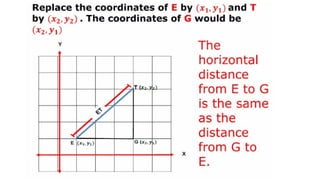
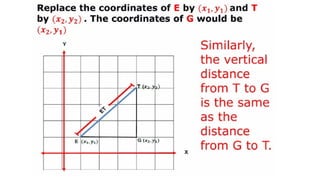
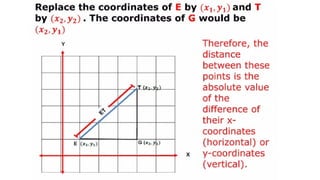
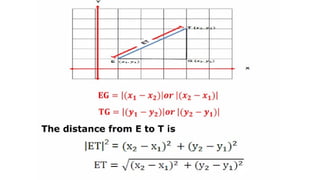







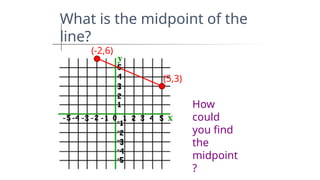




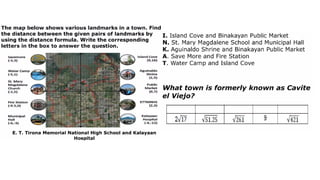








DISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS FORMDISTANCE FORMULA and CENTER-RADIUS F







































