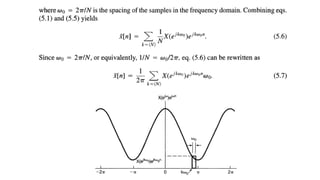
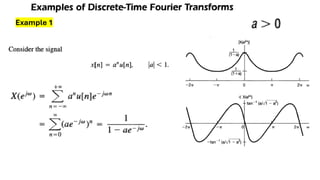
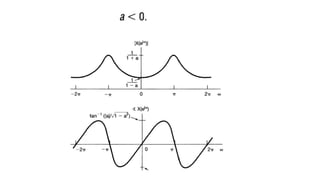
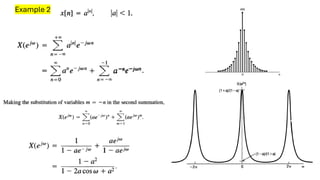
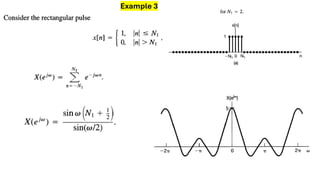
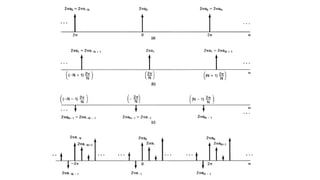
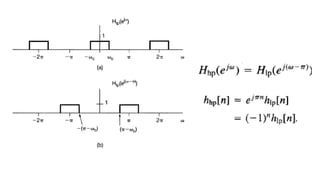
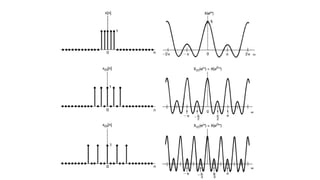
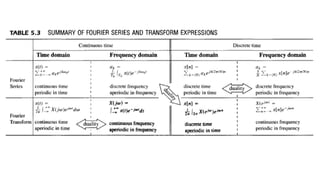
The document discusses the discrete time Fourier transform (DTFT) representation of discrete time aperiodic signals as combinations of complex exponentials, highlighting the transformation from time to frequency domain. It differentiates between periodic and aperiodic convolution regarding integral evaluation, with the former being evaluated over a length of 2π. Several examples are provided to illustrate these concepts.

1. Discrete Time Fourier
Transform (DTFT)
Representation of Discrete Time Aperiodic Signals as a linear
combination of complex exponentials
Transforming Discrete signals from time domain to frequency
domain

6. Example 1

8. Example 2

9. Example 3

14. Example

25. It corresponds to a periodic convolution of and the
integral in this equation can be evaluated over any interval of length 2Π . The usual
form of convolution (in which the integral ranges from -infinity to +infinity) is often
referred to as aperiodic convolution to distinguish it from periodic convolution.

38. Thank you