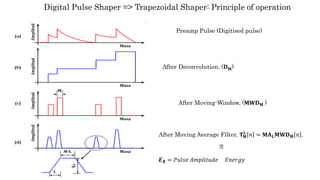
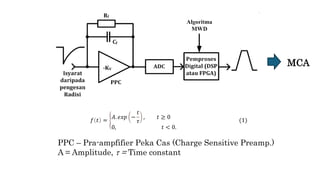
The document discusses a digital pulse processing technique utilizing moving window deconvolution (MWD) for enhanced signal resolution and reduced noise in pulse measurements. It explains the mathematical framework behind MWD, including algorithm components and comparisons between trapezoidal and triangular shaping methods. Key references are provided to foundational studies in digital pulse processing and signal conditioning.

1. Digital Pulse
Processor
Moving Window Deconvolution (MWD)

2. 𝑓 𝑡 =
𝐴. 𝑒𝑥𝑝 −
𝑡
𝜏
, 𝑡 ≥ 0
0, 𝑡 < 0.
(1)
PPC – Pra-ampfifier Peka Cas (Charge Sensitive Preamp.)
A = Amplitude,  = Time constant
MCA

3. Digital Pulse Shaper => Trapezoidal Shaper
Why? : Superior noise figure (High resolution), reduces ballistic
deficit &
excellent baseline stabilitiy @ high count-rate.
Algorithm:
Moving-Window Deconvolution (MWD) – Georgiev & Gast 1992,
Jordanov & Knoll (1993), Martin Lauer (2004)
Initial Pulse amplitude can be obtained at Amplitude at
any point within the signal by knowing the decay time &
starting point of the signal
A = 𝑓 𝑡𝑛 +
1
𝜏 ∞
𝑡𝑛
𝑓 𝑡 𝑑𝑡. <−− − Analogue domain
𝑓 𝑡𝑛 = Amplitude at time, 𝑡𝑛, 𝜏 = 𝑑𝑒𝑐𝑎𝑦 𝑡𝑖𝑚𝑒 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
𝐴 𝑛 = 𝑥 𝑛 +
1
𝜏𝑠
𝑘=−∞
𝑛−1
𝑥 𝑘 = 𝑥 𝑛 − 1 −
1
𝜏𝑠
𝑥 𝑛 − 1 + 𝐴 𝑛 − 1 , 2 . . 𝐷𝑖𝑔𝑖𝑡𝑎𝑙 𝑑𝑜𝑚𝑎𝑖𝑛
𝜏𝑠 = sampling time

4. Digital Pulse Shaper => Trapezoidal Shaper
𝐴 𝑛 = 𝑥 𝑛 +
1
𝜏𝑠
𝑘=−∞
𝑛−1
𝑥 𝑘 = 𝑥 𝑛 − 1 −
1
𝜏𝑠
𝑥 𝑛 − 1 + 𝐴 𝑛 − 1 , 2 . . 𝐷𝑖𝑔𝑖𝑡𝑎𝑙 𝑑𝑜𝑚𝑎𝑖𝑛
𝜏𝑠 = sampling time
Differentiation of (2) with moving window with width M yield MWD
equation:
𝐌𝐖𝐃𝐌 𝑛 = 𝐴 𝑛 − 𝐴 𝑛 − M = 𝑥 𝑛 − 𝑥 𝑛 − M +
1
𝜏𝑠
𝑘=𝑛−M
𝑛−1
𝑥 𝑘 (3).
With Deconvolution 𝐃𝐌 𝑛 = 𝑥 𝑛 − 𝑥[𝑛 − M] & Moving window 𝑛 =
𝑘=𝑛−M
𝑛−1
𝑥[𝑘] 𝐌𝐀𝐌
Eq.(3) deduced to:-
𝐌𝐖𝐃𝐌 𝑛 = 𝐃𝐌 𝑛 +
1
𝜏𝑠
𝐌𝐀𝐌 𝑛
MWD does not filter the noise? Need low-pass filter i.e., Moving Average
with sampling L (𝐌𝐀𝐋). Pulse , 𝐓𝐌
𝐋
𝑛 = 𝐌𝐀𝐋𝐌𝐖𝐃𝐌 𝑛 .
if L = M -> Triangular Shaper, L  M  Trapezoid Shaper (Flat top width
= M-L)

5. Digital Pulse Shaper => Trapezoidal Shaper: Principle of operation
Preamp Pulse (Digitised pulse)
After Deconvolution, (𝐃𝐌)
After Moving-Window, (𝐌𝐖𝐃𝐌 )
After Moving Average Filter, 𝐓𝐌
𝐋
𝑛 = 𝐌𝐀𝐋𝐌𝐖𝐃𝐌 𝑛 .
𝑬𝑹 = 𝑃𝑢𝑙𝑠𝑒 𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒 𝐸𝑛𝑒𝑟𝑔𝑦

6. Useful readings:
1. Jordanov, V., dan G. F. Knoll. 1993. Digital pulse processor using
moving average technique. Nuclear Science, IEEE Transactions on
40 (4):764-769
2. Georgiev, A., dan W. Gast. 1992. Digital pulse processing in high-
resolution, high-throughput, gamma-ray spectroscopy. Nuclear
Science Symposium and Medical Imaging Conference, 1992.,
Conference Record of the 1992 IEEE, 25-31 Oct 1992.
3. Lauer, Martin. 2004. PhD Thesis, Digital Signal Processing for
segmented HPGe Detectors: Preprocessing Algorithms and Pulse
Shape Analysis, Max-Planck-Insitut für Kernphysik, University of
Heidelberg, Heidelberg.