Downloaded 58 times
Uploaded byXiaomeng Chai
Data Mining Case Study
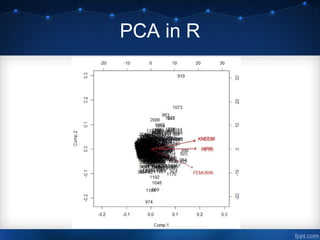
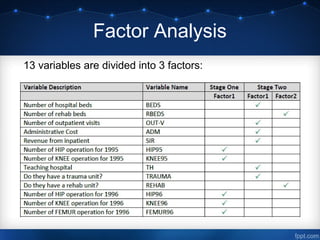
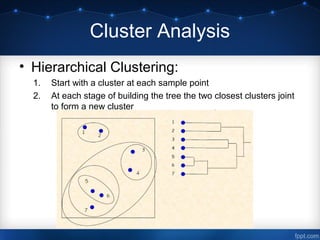
This document discusses using data mining techniques to analyze hospital data and increase sales of orthopedic equipment. It analyzes data on U.S. hospitals from selected midwestern states to identify target hospital segments. Dimension reduction using factor and principal component analysis identifies key factors related to operations, size, and rehabilitation. Cluster analysis segments hospitals into groups using hierarchical and k-means clustering. Regression analysis identifies hospitals with high sales potential based on their current sales levels. The overall aim is to use data mining to select hospital market segments to focus sales efforts on for increasing orthopedic equipment sales.
More Related Content
![Introduction to Pandas and Time Series Analysis [PyCon DE]](https://cdn.slidesharecdn.com/ss_thumbnails/introductiontopandasandtimeseriesanalysispyconde-170617163724-thumbnail.jpg?width=640&height=640&fit=bounds)
Data Mining Case Study
- 1. Sales of OrthopedicEquipment Xiaomeng (Mina) Chai 11/25/2014
- 2. Client’s Background • Client: alarge manufacturer of orthopedic equipment in the United States • Customer base: almost all hospitals over the 50 states
- 3. Client’s Products • Orthopedicparts and equipment • Medications administered in the process of surgery, rehabilitation, and recovery
- 4. The Company Thinks… • SALES! – High sales – Moderate sales (further sales potential) – Little or no sales (substantial potential gain)
- 5.
- 6. We think… • ORTHOPEDICACTIVITIES! – Small general hospitals (little or no interest) – Large general hospitals (moderate interest) – Specialized hospitals (main target group!)
- 7. Objective • Increase sales... …inthe more desirable groups! • How? – Identify target hospitals – Study them individually • Another objective: other ways to classify hospitals?
- 8. Dataset All U.S. hospitalsare in the dataset:
- 9. Variables A subset ofvariables is already selected
- 10.
- 11. Methodology • Data Mining –Dimension Reduction • Factor Analysis • Principal Component Analysis – Cluster Analysis • Hierarchical Clustering • Centroid Methods • Regression analysis
- 12. Data Mining • Overallgoal—to extract information from a data set and transform it into an understandable structure for further use. (Wikipedia) • The objective of data mining is to identify nuggets, small clusters of observations in these data that contain unexpected, yet potentially valuable, information. (The author)
- 13.
- 14. Approach to datamining 1. Dimension (variable) reduction – Principle components – Factor analysis 1. Data segmentation and selection – Cluster analysis – Tree methods – Neural nets 1. Data analysis of interesting segments
- 15.
- 16. PART 1:Select MarketSegments • Find state or group of states (at least 300 hospitals) – IL, IN, MI, WI are selected (590 hospitals)
- 17. Transformation Log or squareroot transformations are performed
- 18.
- 19.
- 20. Dimension Reduction • Twostages factor analysis – Operational factor (HIP95, KNEE95, HIP96, KNEE96, and FEMUR96) – Size factor (BEDS, OUTV, ADM, SIR, TH, and TRAUMA) and rehab factor (RBEDS and REHAB)
- 21.
- 22.
- 23. Factor Analysis: Rotate? •More interpretable results. • Orthogonal rotation methods (VARIMAX) is commonly used. e.g. Look at variable X33 here:
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36. Factor Analysis 13 variablesare divided into 3 factors:
- 37. Textbook Question: Graph themain principal components. Are there any visible clusters? The banding is relatively vertical, REHAB is affecting factor 2 (RBEDS and REHAB).
- 38.
- 39. Cluster Analysis • Todetermine the best cluster to concentrate on for improving sales. • Two popular methods – Hierarchical Clustering (interpoint distance) • Single linkage • Average linkage • Ward – Centroid Methods • K-means algorithm • Partitioning Around Medoids (PAM)
- 40. Cluster Analysis • HierarchicalClustering: 1. Start with a cluster at each sample point 2. At each stage of building the tree the two closest clusters joint to form a new cluster
- 41. Cluster Analysis • CentroidMethods (K-means algorithm) 1. K seed points are chosen and the data is distributed among k cluster 2. At each step, switch a point from one cluster to another if the R2 is increased 3. Clusters are slowly optimized by switching points until no improvement of the R2 is possible
- 42. Cluster Analysis • CentroidMethods (K-means algorithm)
- 43. Cluster Analysis • PartitioningAround Medoids (PAM) 1. Search for k representative medoids 2. K clusters are constructed by assigning each point to the nearest medoid 3. The goal is to find k medoids which minimize the sum of the dissimilarities of the observations to their closest representative medoid.
- 44. Cluster Analysis • PAMVS K-means – PAM operates on the dissimilarity matrix – PAM minimizes a sum of dissimilarities instead of a sum of squared Euclidean distances – Silhouette plot (select the optimal number of clusters)
- 45. Cluster Analysis • Todetermine the best cluster to concentrate on for improving sales. • Two popular methods – Hierarchical Clustering (interpoint distance) • Single linkage • Average linkage • Ward – Centroid Methods • K-means algorithm • Partitioning Around Medoids (PAM)
- 46.
- 47.
- 48.
- 49. PAM in R •Silhouette width: si=(bi-ai)/max(ai,bi) Large Si (almost 1) are very well clustered
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56. Part 2-Estimate PotentialSales • Part1 – Select Market Segments : DONE • Part2 – Estimate Potential Sales
- 57.
- 58.
- 59. Regression Analysis • Hospitalswith large negative residuals: HID CITY STATE RESIDUAL Gain 087043 Chicago IL -2.8766 68.590 915042 South Bend IN -1.7989 16.440 016045 Beloit WI -2.5633 24.893 020042 Columbus IN -2.5146 34.710 078045 Madison WI -2.2309 59.362 109043 Chicago IL -1.9317 47.980 262043 Peoria IL -2.5952 90.593
- 60. Thank you andHappy Holiday!
Editor's Notes
- #4 Orthopedic equipment refers to a variety of structural devices designed to stabilize, protect, and/or correct orthopedic disorders. Common medications used to treat orthopedic conditions include nonsteroidal anti-inflammatory medications (e.g. Motrin, Aleve, Naprosyn, Celebrex), Glucosamine, and others.
- #5 From the point of view of sales
- #7 From the point of view of activities
- #9 4703 hospitals and 19 variables Chicago has 45 hospitals
- #16 From raw data to small dataset
- #18 Independent var—linear trend Dependent var--normality
- #24 The elements of the Factor Pattern reflect the unique variance each factor contributes to the variance of an observed variable. The reason factor analysis is not stopped after this initial factoring stage, without rotating the factors, is that the factors as they currently exist are not easily interpretable. In an ideal solution, the variables should “load” highly (have a high value that approaches 1) on just one factor each.
- #25 Final Conmmunality Estimates: It can be derived by taking sum of squares of each row of the factor pattern. This is the variance of the observed variable that is accounted for by each factor.
- #34 The left and bottom axes are showing the loadings; the top and right axes are showing principal component scores. meaningful visual representation of the structure of cases and variables.
- #47 Cluster History section starts out with n (590) clusters of size 1 and continues until all the obs are included into one cluster. R^2: the proportion of variance explained by a particular cluster. In the first step, n-1 clusters are formed, R^2 are then computed to have the largest R^2. So the largest R^2 will form the first cluster. Thus, at each step of the algorithm clusters or observations are combined in such a way as to maximize the r2 value. the biggest jump between cluster 5 and 4 with almost 0.1 difference. Therefore, I chose 5 clusters for my future analysis.
- #50 Put a(i) = average dissimilarity between i and all other points of the cluster to which i belongs (if i is the only observation in its cluster, s(i) := 0 without further calculations). For all other clusters C, put d(i,C)= average dissimilarity of i to all observations of C. The smallest of these d(i,C) is b(i) := \min_C d(i,C), and can be seen as the dissimilarity between i and its “neighbor” cluster, i.e., the nearest one to which it does not belong. Finally,