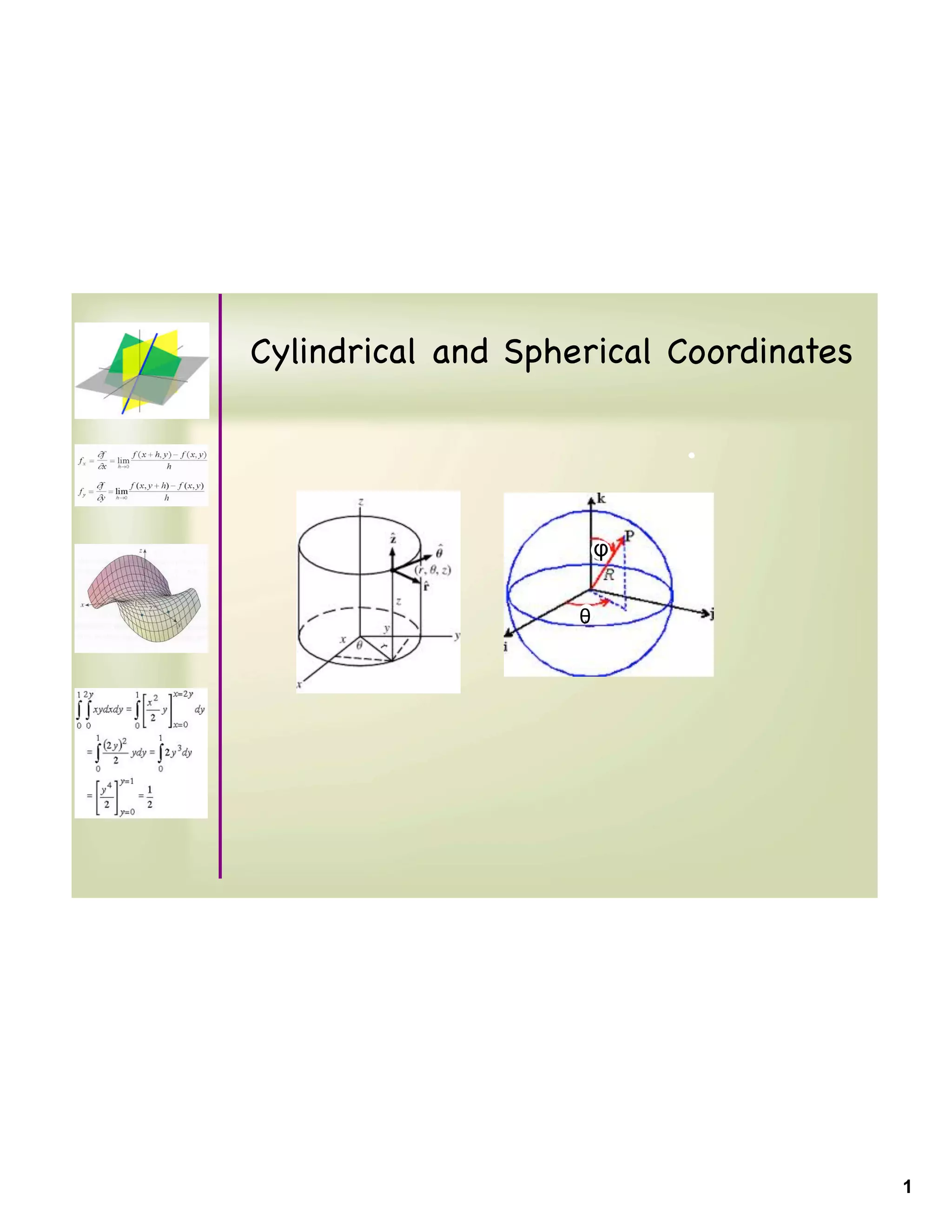
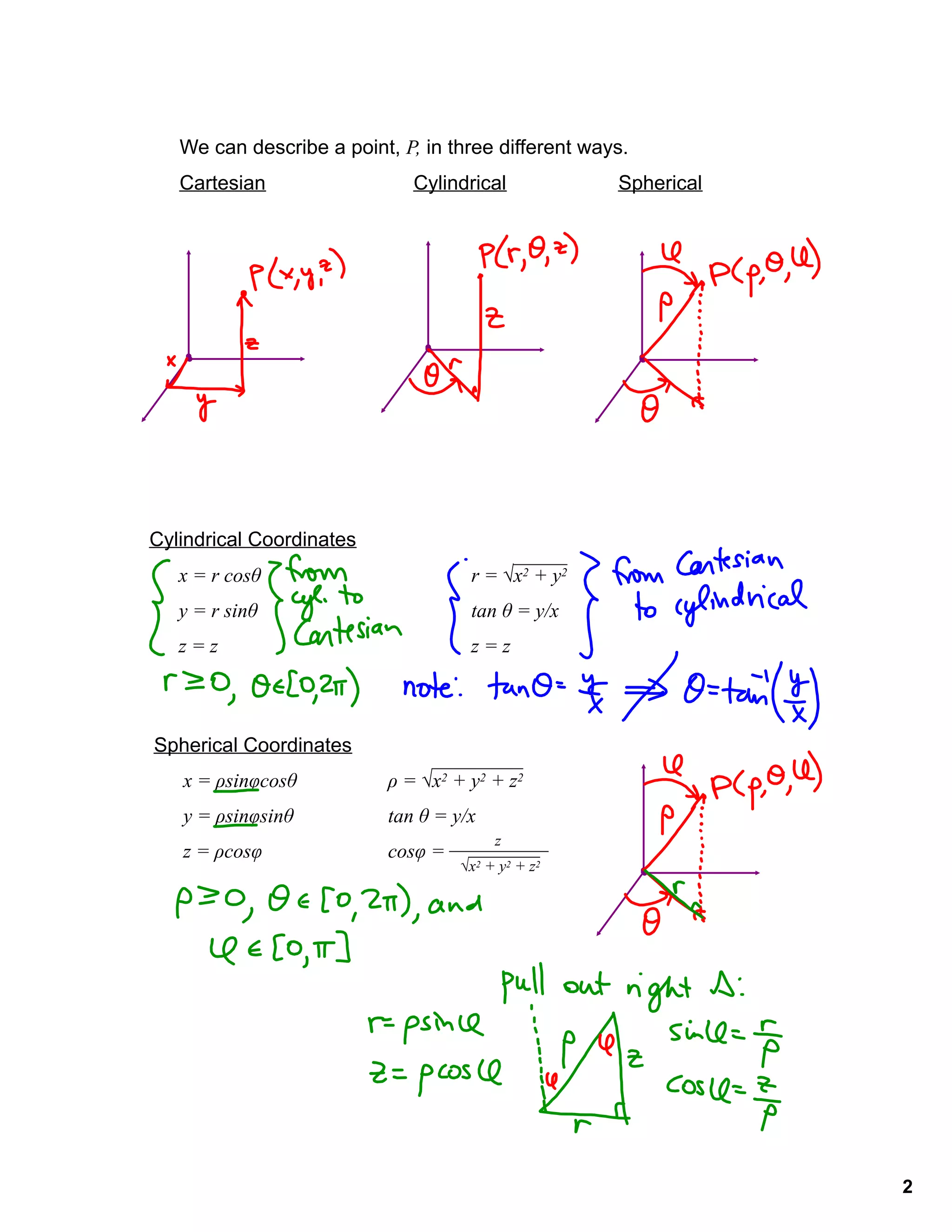
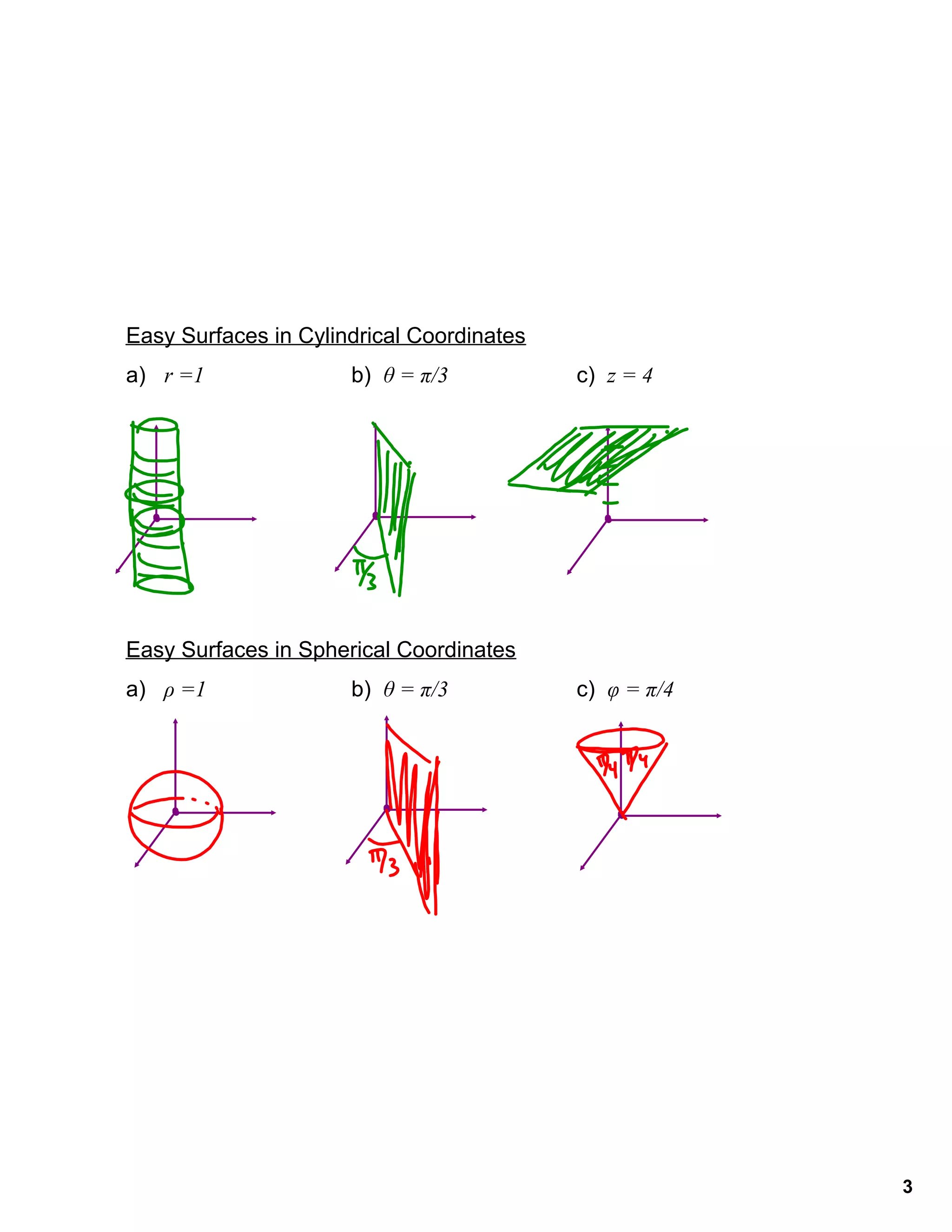
The document discusses three coordinate systems - Cartesian, cylindrical, and spherical coordinates. It provides the equations to convert between the three systems, gives examples of basic surfaces defined in each system, and includes practice problems to convert coordinates between systems and change equations into different coordinate representations.

1. 1
Cylindrical and Spherical Coordinates
θ
φ

2. 2
We can describe a point, P, in three different ways.
Cartesian Cylindrical Spherical
Cylindrical Coordinates
x = r cosθ r = √x2 + y2
y = r sinθ tan θ = y/x
z = z z = z
Spherical Coordinates
x = ρsinφcosθ ρ = √x2 + y2 + z2
y = ρsinφsinθ tan θ = y/x
z = ρcosφ cosφ =
√x2 + y2 + z2
z

3. 3
Easy Surfaces in Cylindrical Coordinates
a) r =1 b) θ = π/3 c) z = 4
Easy Surfaces in Spherical Coordinates
a) ρ =1 b) θ = π/3 c) φ = π/4

4. 4
EX 1 Convert the coordinates as indicated
a) (3, π/3, -4) from cylindrical to Cartesian.
b) (-2, 2, 3) from Cartesian to cylindrical.

5. 5
EX 2 Convert the coordinates as indicated
a) (8, π/4, π/6) from spherical to Cartesian.
b) (2√3, 6, -4) from Cartesian to spherical.

6. 6
EX 3 Convert from cylindrical to spherical coordinates.
(1, π/2, 1)

7. 7
EX 4 Make the required change in the given equation.
a) x2 - y2 = 25 to cylindrical coordinates.
b) x2 + y2 - z2 = 1 to spherical coordinates.
c) ρ = 2cos φ to cylindrical coordinates.

8. 8
EX 4 Make the required change in the given equation (continued).
d) x + y + z = 1 to spherical coordinates.
e) r = 2sinθ to Cartesian coordinates.
f) ρsin θ = 1 to Cartesian coordiantes.