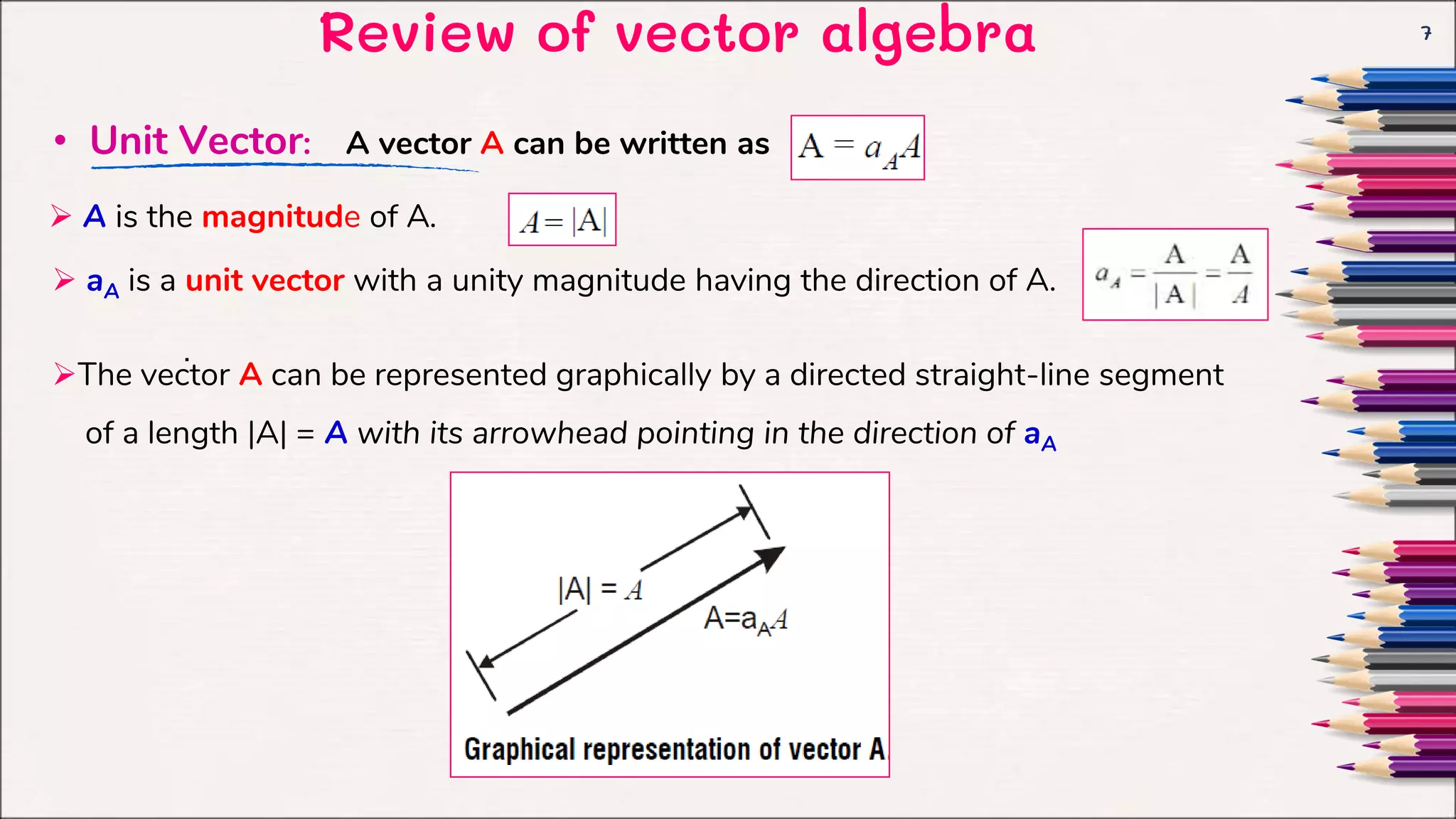
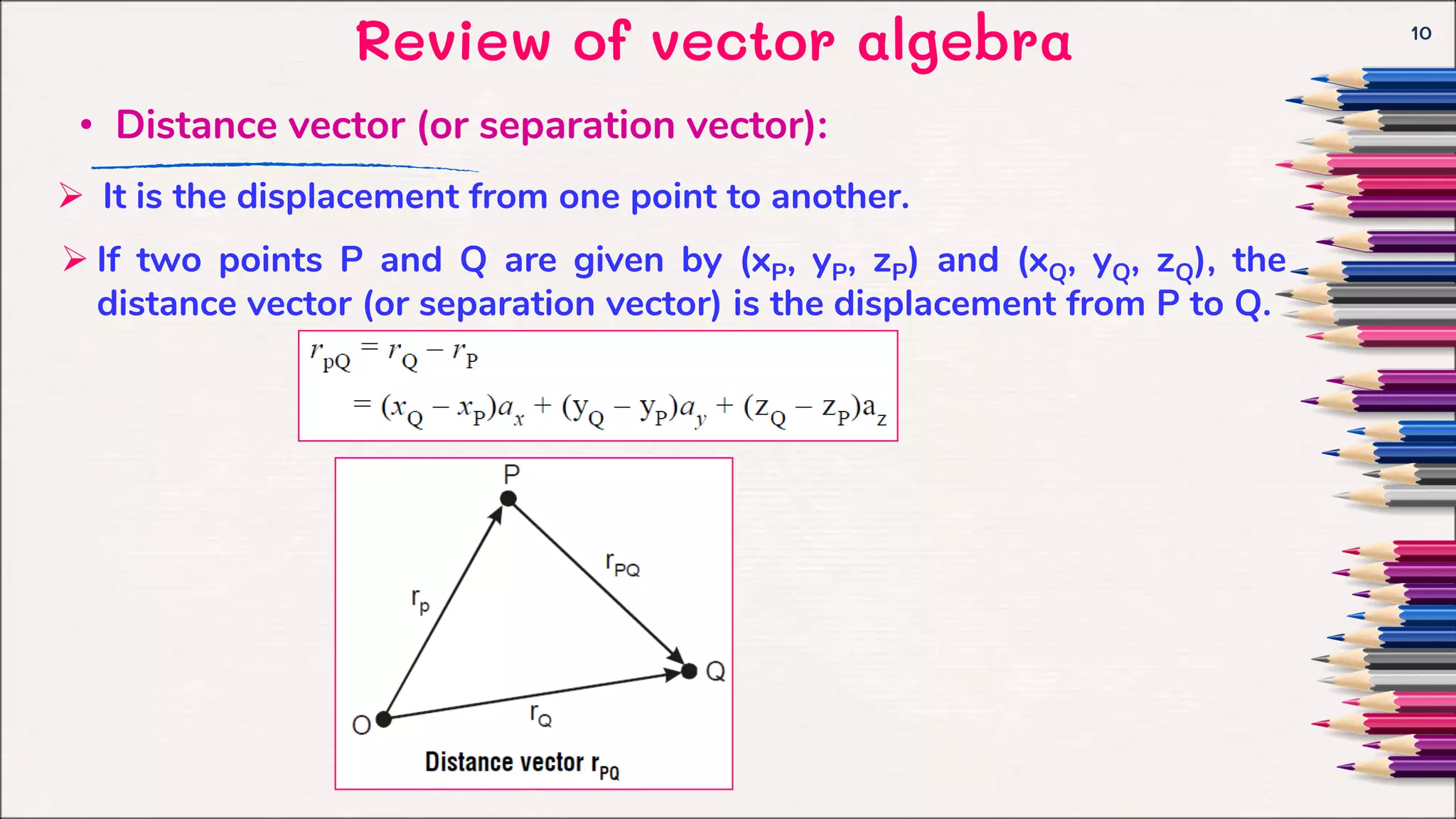
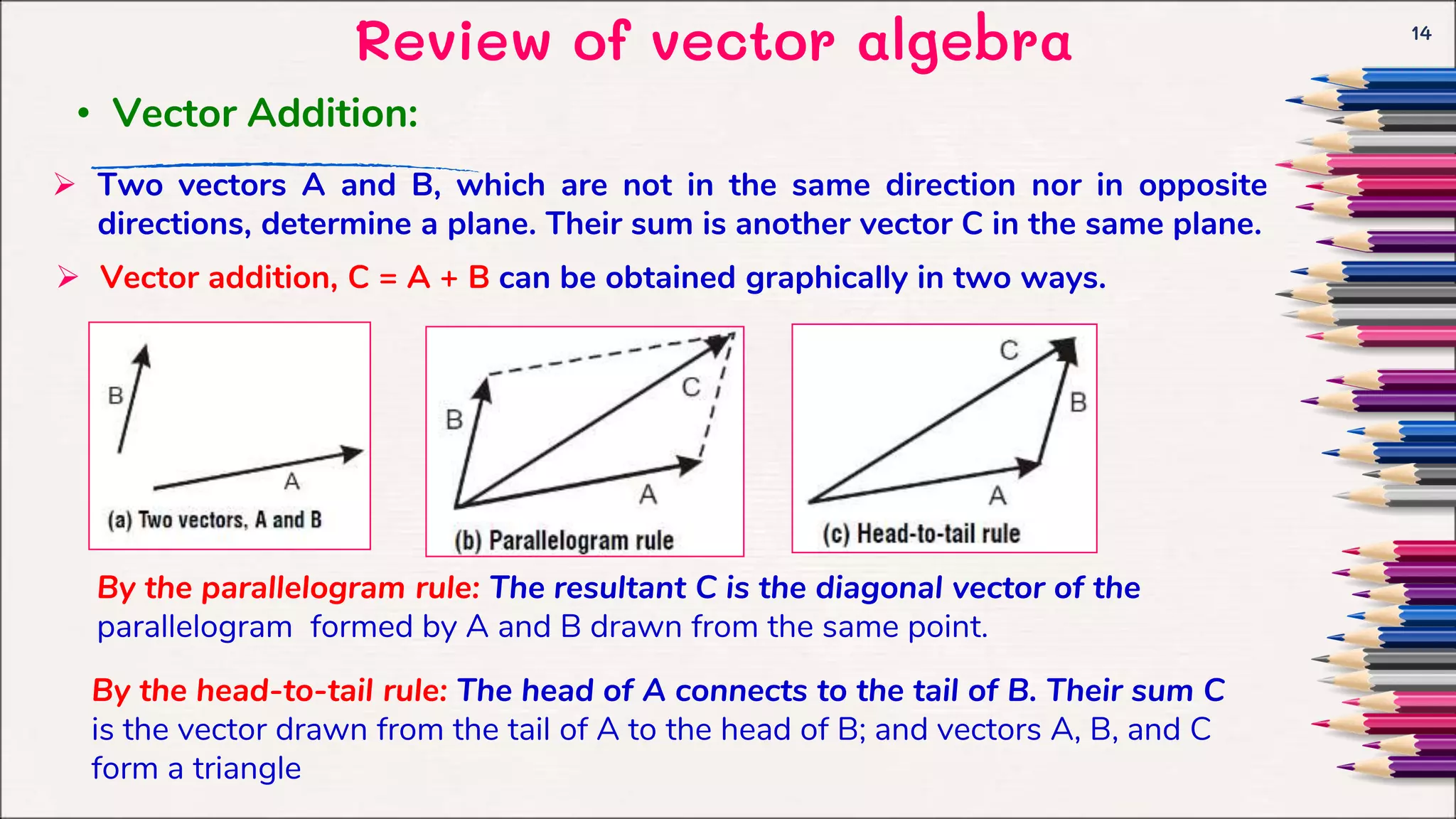
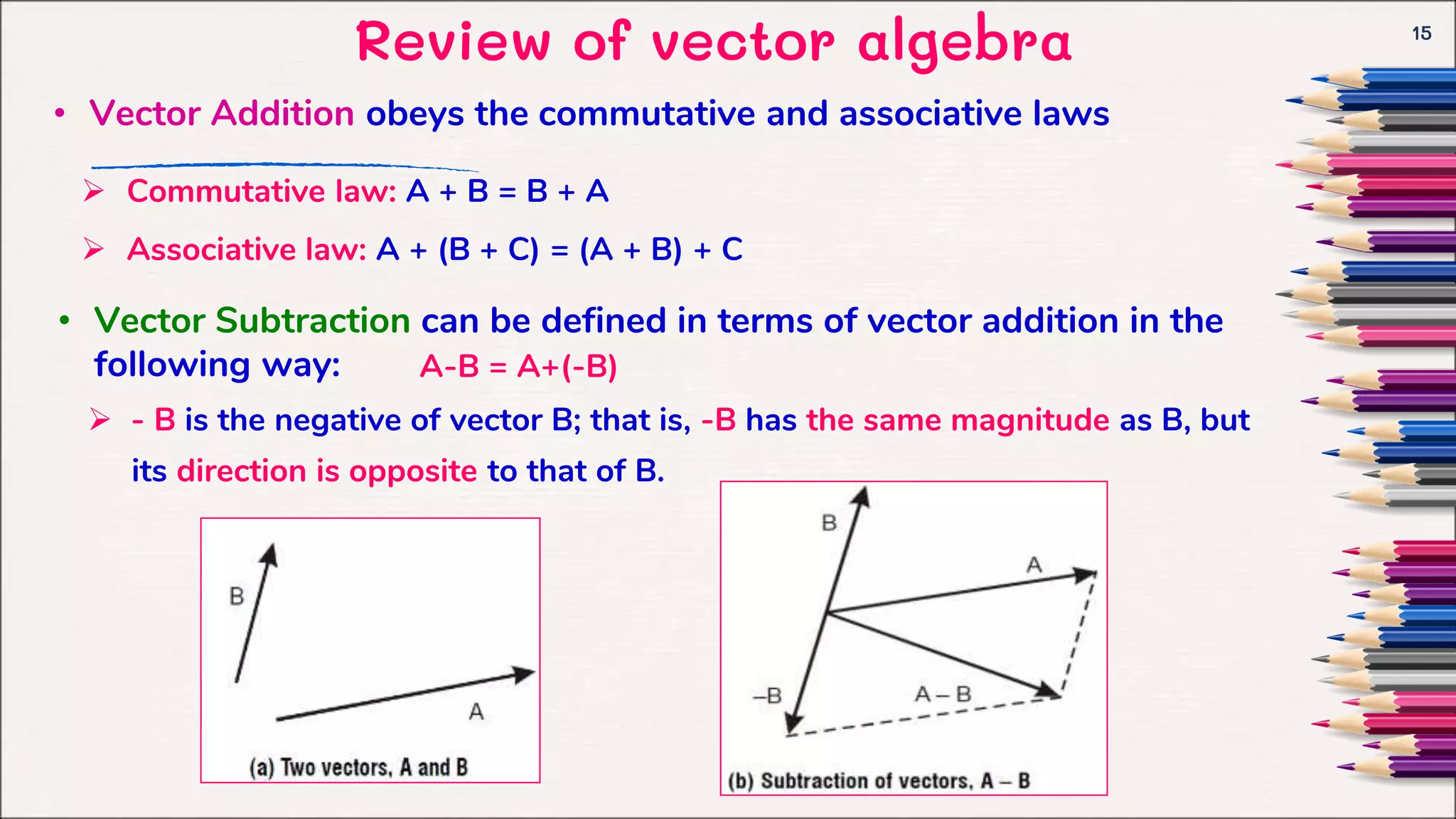
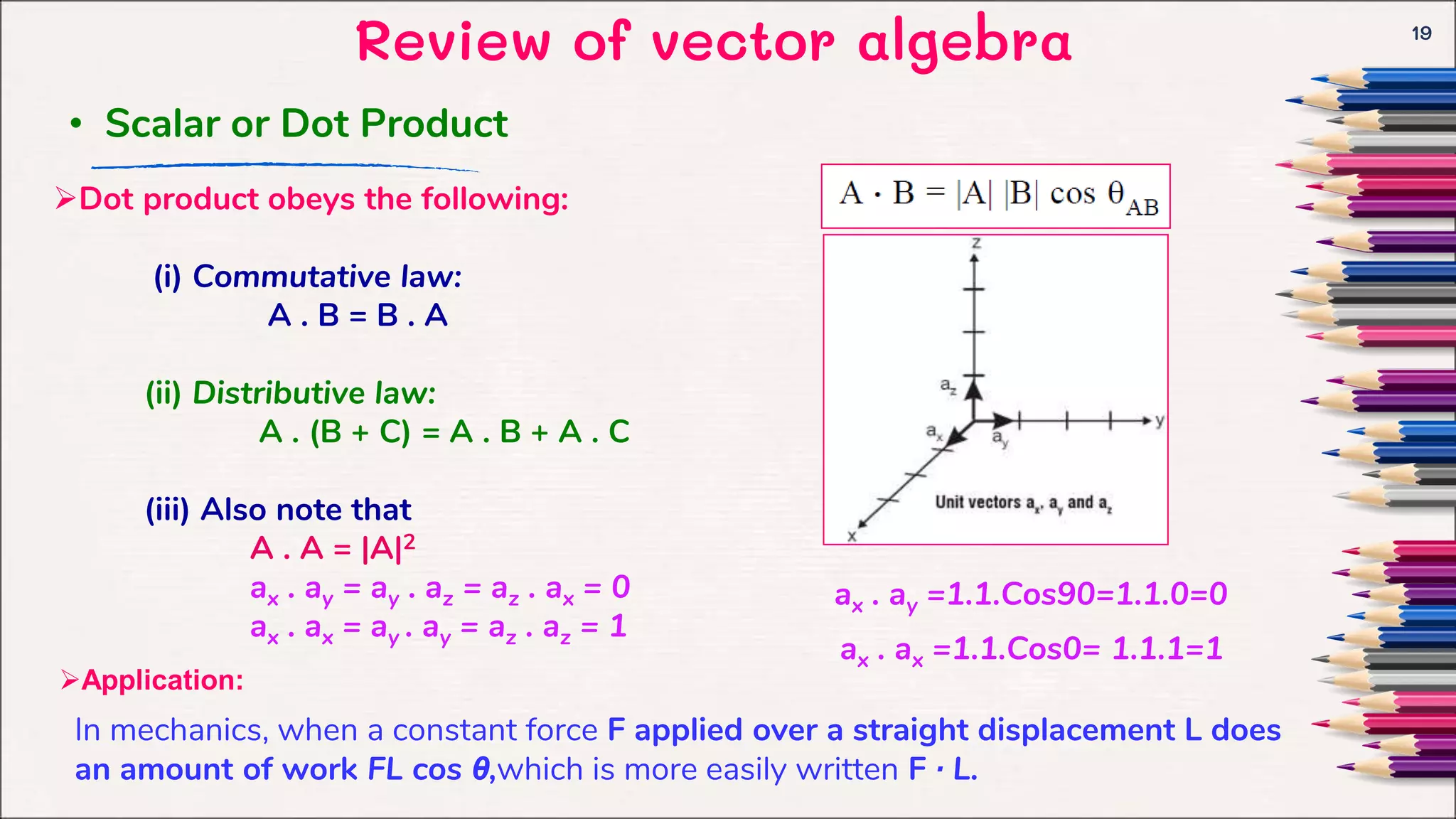
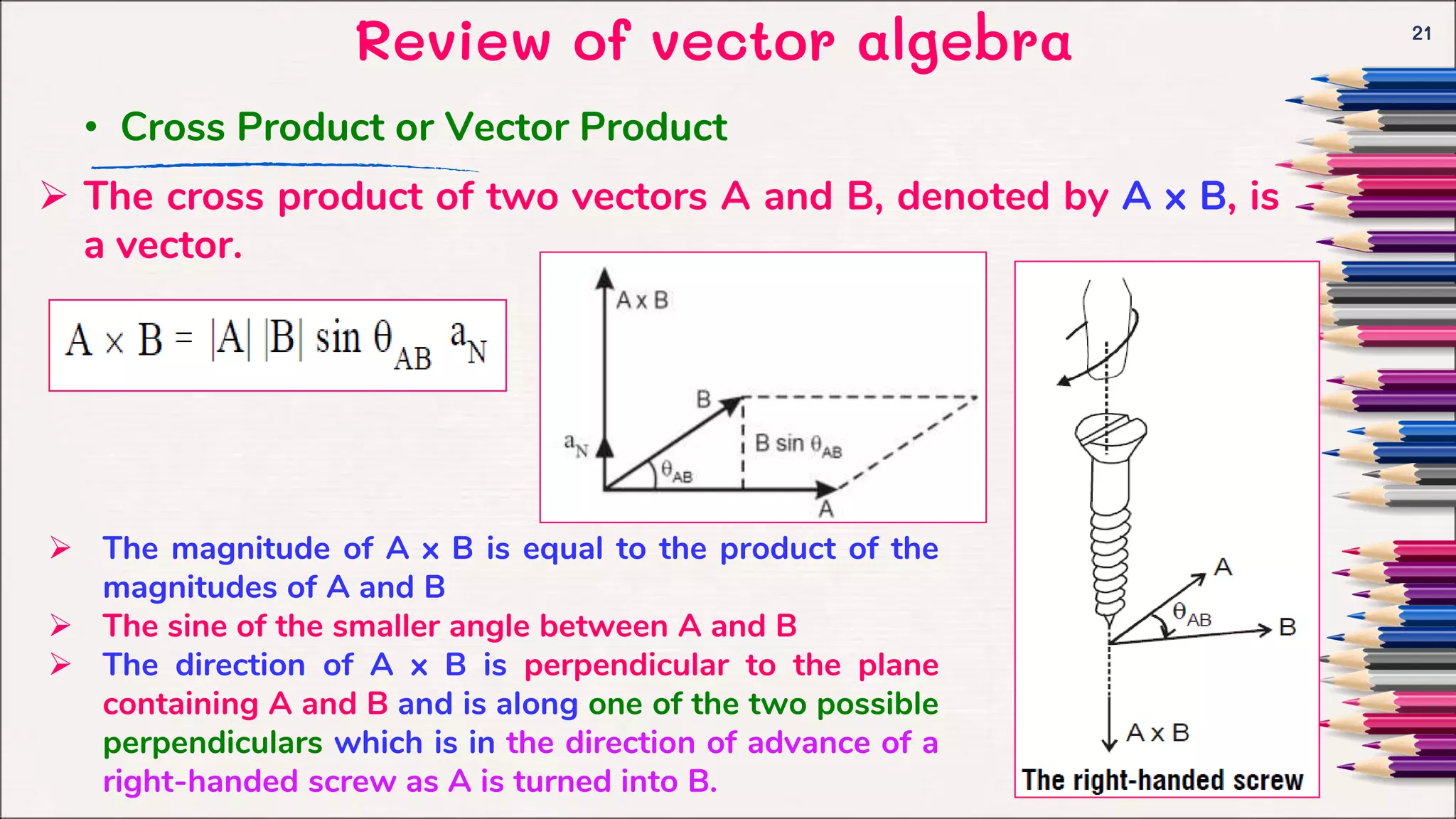
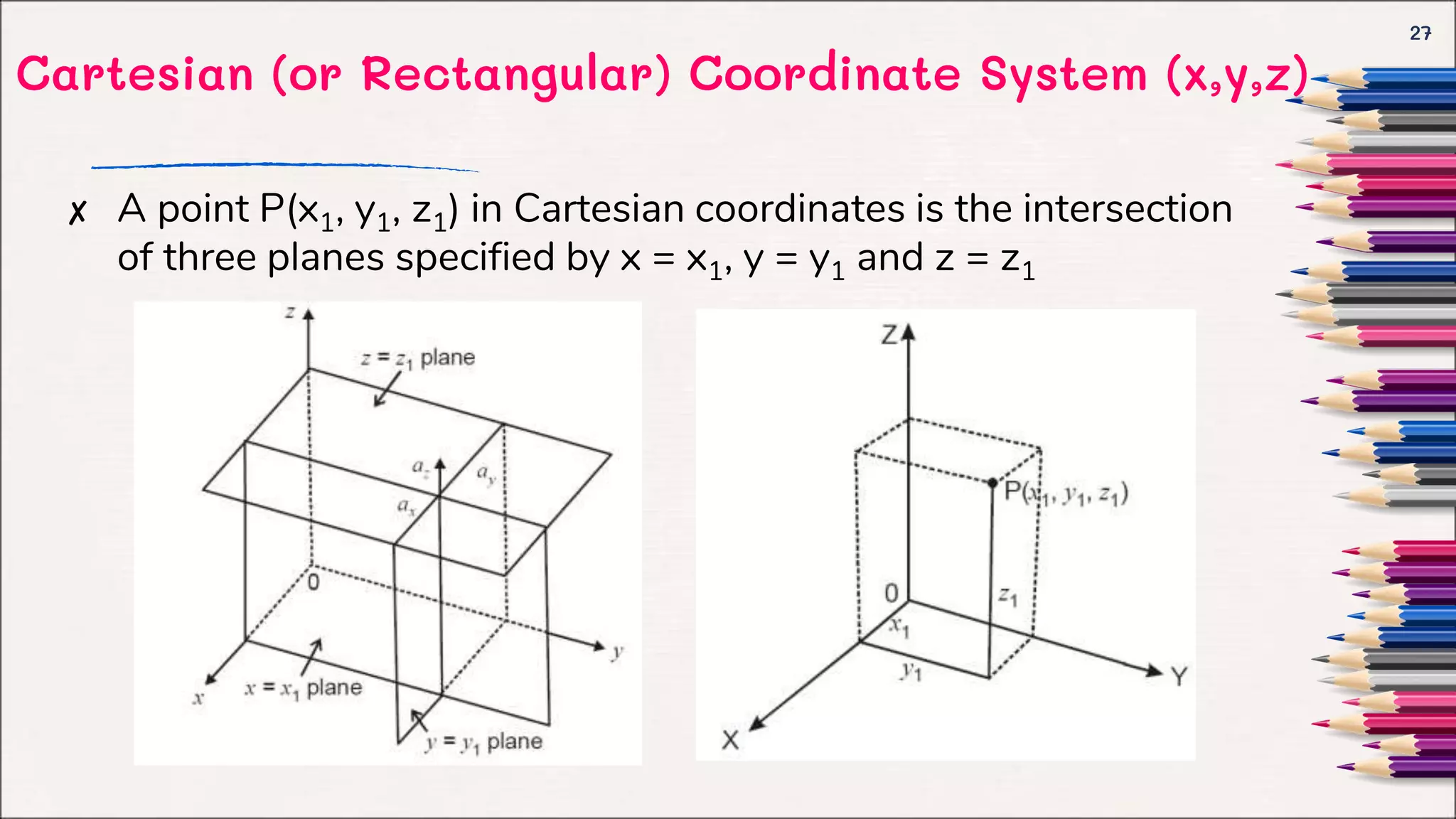
This document provides an introduction to electromagnetic fields and vector algebra concepts. It begins with an overview of vector algebra topics like vector addition, multiplication of vectors by scalars, and dot and cross products. It then discusses orthogonal coordinate systems, focusing on Cartesian coordinates. The document provides examples and solved problems for various vector algebra concepts. It aims to review key vector algebra that will be used as a mathematical tool for electromagnetic concepts.

1. EC8451- ELECTROMAGNETIC FIELDS
Dr.K.G.SHANTHI
Professor/ECE
shanthiece@rmkcet.ac.in
Review of vector algebra-Problems
•Unit Vector, Position Vector, Distance vector
•Vector Addition
•Multiplication of a Vector by a Scalar
•Scalar or dot product: A • B
•Vector or cross product: A x B
Orthogonal Coordinate Systems-Introduction

2. ✘ Electromagnetics is a branch of physics or electrical engineering that
deals electric and magnetic phenomena.
✘ Electromagnetics is the study of the effects of electric charges at rest
and in motion.
✘ Both positive and negative charges are sources of an electric field.
✘ Moving Charges produce a current, which gives rise to a magnetic field.
✘ A Field is a spatial distribution of a quantity, which may or may not be a
function of time. A time-varying electric field is accompanied by a
magnetic field, and vice versa resulting in electromagnetic field.
✘ Circuit theory Vs Field theory
✘ Inductive Approach Vs Deductive approach
✘ Electromagnetic model
✘ Units and Constants
2
UNIT-I: INTRODUCTION

3. Review of vector algebra
3
.
• Vector analysis is mathematical shorthand.
• Vector analysis is a mathematical tool with which
electromagnetic (EM) concepts are most conveniently expressed
and best comprehended.
• Three main topics on vector analysis are as follows:
1. Vector algebra – addition, subtraction, and multiplication of vectors.
2. Orthogonal coordinate systems – Cartesian, cylindrical, and spherical
Coordinates.
3. Vector calculus – differentiation and integration of vectors; line,
surface, and volume integrals;“del” operator; gradient, divergence,
and curl operations.

4. Review of vector algebra
4
.
• Scalar: At a given time and position, a scalar is completely
specified by its magnitude. The term scalar refers to a quantity
whose value may be represented by a single (positive or
negative) real number.
• Examples:
• A body falling a distance L in a time t
• The temperature T at any point in a bowl of soup whose
coordinates are x, y, and z
Here L, t, T, x, y, and z are all scalars.
• Other scalar quantities are mass, density, pressure, volume,
charge, electric potential, voltage and population.

5. Review of vector algebra
5
.
• Vector: The specification of a vector at a given
location and time requires both a magnitude
and a direction.
• Examples:
• Force, velocity, acceleration, displacement,
electric field intensity and a straight line from
the positive to the negative terminal of a
storage battery are examples of vectors.

6. Review of vector algebra
6
.
• Field:
A field is a function that specifies a particular quantity
everywhere in a region. The value of a field varies in general
with both position and time.
• Both scalar fields and vector fields exist.
• The temperature throughout the bowl of soup, temperature
distribution in a building, sound intensity in a theater are
examples of scalar fields.
• The gravitational force on a body in space, the velocity of
raindrops in the atmosphere are examples of vector fields.

7. Review of vector algebra 7
.
• Unit Vector: A vector A can be written as
 A is the magnitude of A.
The vector A can be represented graphically by a directed straight-line segment
of a length |A| = A with its arrowhead pointing in the direction of aA
 aA is a unit vector with a unity magnitude having the direction of A.

8. Review of vector algebra
8
.
 A vector A in Cartesian (or rectangular) coordinates may be represented as
where Ax, Ay, and Az are called the components of A in the x, y, and z directions respectively;
ax, ay and az are unit vectors in the x, y, and z directions, respectively.
The magnitude
of vector A is
given by
The unit vector along A is given by

9. Review of vector algebra 9
.
• Position Vector:
 A point P in Cartesian coordinates may be represented by (x, y, z).
 The position vector rp (or radius vector) of point P is defined as the
directed distance from the origin O to P given by

10. Review of vector algebra 10
• Distance vector (or separation vector):
 It is the displacement from one point to another.
 If two points P and Q are given by (xP, yP, zP) and (xQ, yQ, zQ), the
distance vector (or separation vector) is the displacement from P to Q.

11. SOLVED PROBLEMS-vector algebra 11

12. SOLVED PROBLEMS-vector algebra 12

13. SOLVED PROBLEMS-vector algebra 13
Specify the unit vector extending from the origin toward the point
G( 2, –2, –1).
Solution:

14. Review of vector algebra 14
• Vector Addition:
 Two vectors A and B, which are not in the same direction nor in opposite
directions, determine a plane. Their sum is another vector C in the same plane.
 Vector addition, C = A + B can be obtained graphically in two ways.
By the parallelogram rule: The resultant C is the diagonal vector of the
parallelogram formed by A and B drawn from the same point.
By the head-to-tail rule: The head of A connects to the tail of B. Their sum C
is the vector drawn from the tail of A to the head of B; and vectors A, B, and C
form a triangle

15. Review of vector algebra 15
• Vector Addition obeys the commutative and associative laws
 Commutative law: A + B = B + A
 Associative law: A + (B + C) = (A + B) + C
 - B is the negative of vector B; that is, -B has the same magnitude as B, but
its direction is opposite to that of B.
• Vector Subtraction can be defined in terms of vector addition in the
following way: A-B = A+(-B)

16. Review of vector algebra 16
• Multiplication of a Vector by a Scalar:
 Multiplication of a vector A by a positive scalar k changes the magnitude of A
by k times without changing its direction.
 The magnitude of the vector changes, but its direction does not when the scalar is
positive, although it reverses direction when multiplied by a negative scalar.
 Multiplication of a vector by a scalar also obeys the associative and
distributive laws of algebra

17. Review of vector algebra 17
• Vector Multiplication
 When two vectors A and B are multiplied, the result is either a scalar or a
vector depending on how they are multiplied.
 Thus there are two types of vector multiplication:
1. Scalar or dot product: A • B
2. Vector or cross product: A x B
• Scalar or Dot Product
 The scalar or dot product of two vectors A and
B, denoted by A • B, is a scalar, which equals
the product of the magnitudes of A and B and
the cosine of the angle between them.
θAB is the smaller angle between A and B and is less than π radians (180°).

18. Review of vector algebra 18
 If A =(Ax, Ay, Az) and B = (Bx, By, Bz), then
A . B = AxBx + AyBy + AzBz
which is obtained by multiplying A and B component by component.
• Scalar or Dot Product
 Two vectors A and B are said to be orthogonal (or perpendicular) with each
other if A • B =0
Hence A • B =0

19. Review of vector algebra 19
Dot product obeys the following:
(i) Commutative law:
A . B = B . A
(ii) Distributive law:
A . (B + C) = A . B + A . C
(iii) Also note that
A . A = |A|2
ax . ay = ay . az = az . ax = 0
ax . ax = ay . ay = az . az = 1
• Scalar or Dot Product
Application:
ax . ay =1.1.Cos90=1.1.0=0
ax . ax =1.1.Cos0= 1.1.1=1
In mechanics, when a constant force F applied over a straight displacement L does
an amount of work FL cos θ,which is more easily written F · L.

20. Problems on Scalar or Dot Product
20
Dot Product A . B = AxBx + AyBy + AzBz

21. Review of vector algebra 21
 The cross product of two vectors A and B, denoted by A x B, is
a vector.
• Cross Product or Vector Product
 The magnitude of A x B is equal to the product of the
magnitudes of A and B
 The sine of the smaller angle between A and B
 The direction of A x B is perpendicular to the plane
containing A and B and is along one of the two possible
perpendiculars which is in the direction of advance of a
right-handed screw as A is turned into B.

22. Review of vector algebra 22
 If A =(Ax, Ay, Az) and B = (Bx, By, Bz), then
• Cross Product or Vector Product
This is obtained by “crossing” terms in cyclic permutation, hence the name
cross product

23. Review of vector algebra 23
• The Cross Product has the following basic properties:
(i) It is not commutative:
Reversing the order of the vectors A and B results in a unit vector
in the opposite direction.
(ii) It is not associative:
(iii) It is distributive:
(iv)
(v)

24. Problems on Vector Product
24

25. Problems on Vector Product
25
Unit vector normal to the plane:

26. ORTHOGONAL COORDINATE SYSTEMS
 The physical quantities that are being dealt in Electromagnetics are
functions of space and time.
 In a three-dimensiona1 space, a point can be located as the intersection
of three surfaces.
 When these three surfaces are mutually perpendicular to one another,
then it is known as an orthogonal coordinate system.
 An orthogonal system is one in which the coordinates are mutually
perpendicular.
 The three orthogonal coordinate systems that are most common and
useful are:
1. Cartesian (or rectangular) coordinate system
2. Cylindrical coordinate system
3. Spherical coordinate system
26

27. Cartesian (or Rectangular) Coordinate System (x,y,z)
✘ A point P(x1, y1, z1) in Cartesian coordinates is the intersection
of three planes specified by x = x1, y = y1 and z = z1
27

28. Cartesian (or Rectangular) Coordinate System (x,y,z)
28
The unit vectors of the rectangular coordinate system have unit
magnitude and are directed toward increasing values of their
respective variables.

29. 29
THANK YOU