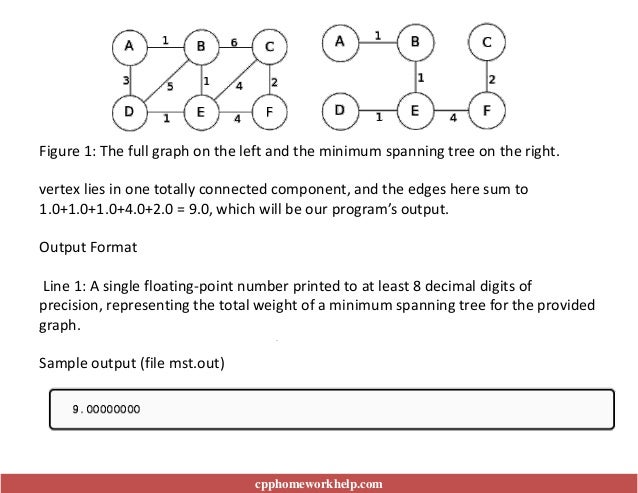
This document discusses implementing Prim's algorithm in C++ using the Standard Template Library to compute a minimum spanning tree (MST) for a graph represented by towns and roads on an island. It outlines the input format, including nodes and edges with weights, and presents a scenario where the goal is to establish affordable internet connectivity. The algorithm relies on a priority queue to find the least total sum of weights of the edges needed to connect all towns.

1. 1
For any help regarding C++ Homework Help
Visit :- https://www.cpphomeworkhelp.com/ ,
Email :- info@cpphomeworkhelp.com or
Call us at :- +1 678 648 4277

2. .
Problems:
The C++ standard template library provides us with a large number of containers and
data structures that we can go ahead and use in our programs. We’ll be learning how to
use a priority queue, which is available in the header.
The problem we can solve using a priority queue is that of computing a minimum
spanning tree. Given a fully connected undirected graph where each edge has a weight,
we would like to find the set of edges with the least total sum of weights. This may
sound abstract; so here’s a concrete scenario:
You’re a civil engineer and you’re trying to figure out the best way to arrange for
internet access in your small island nation of C-Land. There are N (3 ≤ N ≤ 250, 000)
towns on your island connected by M (N ≤ M ≤ 250, 000) various roads and you can walk
between any two towns on the island by traversing some sequence of roads.
However, you’ve got a limited budget and have determined that the cheapest way to
arrange for internet access is to build some fiber-optic cables along existing roadways.
You have a list of the costs of laying fiber-optic cable down along any particular road,
and want to figure out how much money you’ll need to successfully complete the
project–meaning that, at the end, every town will be connected along some sequence
of fiber-optic cables.
cpphomeworkhelp.com

3. .
Luckily, you’re also C-Land’s resident computer scientist, and you remember hearing
about Prim’s algorithm in one of your old programming classes. This algorithm is
exactly the solution to your problem, but it requires a priority queue...and ta-da! Here’s
the C++ standard template library to the rescue. If this scenario is still not totally clear,
look at the sample input description on the next page. Our input data describing the
graph will be arranged as a list of edges (roads and their fiber-optic cost) and for our
program we’ll covert that to an adjacency list: for every node in the graph (town in the
country), we’ll have a list of the nodes (towns) it’s connected to and the weight (cost of
building fiber-optic cable along).
This data structure might be a pain to allocate and keep track of everything in C. The
C++ STL will simplify things. First, our adjacency list can be represented as a list of C++
vectors, one for each node. To further simplify and abstract things, we’ve created a
wrapper class called AdjacencyList that you can use; it already has a method written
to help with reading the input.
Resource Limits
Your program will be allowed up to 3 seconds of runtime and 32MB of RAM.
input Format
cpphomeworkhelp.com

4. Input Explanation
We can visualize this graph as in Figure 1; let A,B,C , . . . represent the nodes with
IDs 0, 1, 2, . . . respectively. Looking at our input file, the we can see that the second
line 0 1 1.0 describes edge between A and B of weight 1.0 in our diagram, the third
line 1 3 5.0 describes the edge between B and D of weight 5.0, and so on. On the
right, we can see a minimum spanning tree for our graph. Every
cpphomeworkhelp.com
Line 1: Two space-separated integers: N , the number of nodes in the graph, and M ,
the number of edges.
Lines 2 . . . M : Line i contains three space-separated numbers describing an edge: si
and ti , the IDs of the two nodes involved, and wi , the weight of the edge.

5. .
Figure 1: The full graph on the left and the minimum spanning tree on the right.
vertex lies in one totally connected component, and the edges here sum to
1.0+1.0+1.0+4.0+2.0 = 9.0, which will be our program’s output.
Output Format
Line 1: A single floating-point number printed to at least 8 decimal digits of
precision, representing the total weight of a minimum spanning tree for the provided
graph.
Sample output (file mst.out)
cpphomeworkhelp.com

6. .
Template Code
If you take a look in the provided template file provided in the file mst.data.zip as a
basis for your program, you’ll see some data structures already written for you.
cpphomeworkhelp.com

7. .
Some questions to ask yourself for understanding:
• What does AdjacencyList() = delete; mean? Why did we do that?
• This is a fairly complicated line:
inline const std::vector& vert( size t node ) const. Justify or question each use of const.
• Why don’t we need to write our own destructor for the AdjacencyList class?
• How large is a single instance of the State class in memory, most likely?
Think these questions through and ask about anything that you’re unsure of on Piazza.
cpphomeworkhelp.com

8. Solutions:
cpphomeworkhelp.com
/* PROG: mst
LANG:
C++ */
#include <vector>
#include <queue>
#include <fstream>
#include <iostream>
#include <iomanip>
#include <unordered_map>
class State { size_t _node; double _dist;
public:
State( size_t aNode, double aDist ) : _node{aNode}, _dist{aDist} {}
inline size_t node()const { return _node; }
inline double dist()const { return _dist; } };
class
AdjacencyList { std::vector< std::vector< State> > _adj; AdjacencyList() = delete;
public:
AdjacencyList( std::istream &input );
inline size_t size() const { return _adj.size(); }
inline const std::vector& adj(size_t node )
const { return _adj[node]; } void print(); };

9. cpphomeworkhelp.com
inline bool operator<( const State &a, const State &b )
{
return a.dist() > b.dist();
}
AdjacencyList::AdjacencyList( std::istream &input ) : _adj{}
{
size_t nNodes; size_t nEdges;
input >> nNodes >> nEdges; _adj.resize( nNodes );
for( size_t e = 0; e < nEdges; ++e )
{
size_t v, w; double weight; input >> v >> w >> weight;
// Add this edge to both the v and w lists
_adj[v].push_back( State{ w, weight } );
_adj[w].push_back( State{ v, weight } );
} }
void AdjacencyList::print()
{
for( size_t i = 0; i < _adj.size(); ++i )
{
std::cout << i << ": ";
for( auto state : _adj[i] )
{
std::cout << "(" << state.node() << ", " << state.dist() << ") ";

10. cpphomeworkhelp.com
}
std::cout << "n";
} }
double prim( const AdjacencyList &adj )
{
std::unordered_map<int, bool> visited;
std::priority_queue<State> pq;
pq.push( State{ 0, 0.0 } );
double weight = 0.0;
while( visited.size() < adj.size() )
{
auto top = pq.top();
pq.pop();
if( visited.count( top.node() ) == 0 )
{
visited[top.node()] = true;
weight += top.dist();
for( auto vertex : adj.adj( top.node() ) )
{
pq.push( vertex );
} } }
return weight;
}

11. int main()
{
std::ifstream input{ "mst.in" };
std::ofstream output{ "mst.out" };
if( input.is_open() )
{
auto adj = AdjacencyList{ input };
output << std::fixed << std::setprecision( 8 );
output << prim( adj ) << "n";
}
else { std::cerr << "Could not open mst.inn"; return 1;
}
return 0;
}
cpphomeworkhelp.com

12. Below is the output using the test data:
mst:
1: OK [0.004 seconds]
2: OK [0.004 seconds]
3: OK [0.004 seconds]
4: OK [0.006 seconds]
5: OK [0.093 seconds]
6: OK [0.122 seconds]
7: OK [0.227 seconds]
8: OK [0.229 seconds]
9: OK [0.285 seconds]
10: OK [0.287 seconds]
cpphomeworkhelp.com