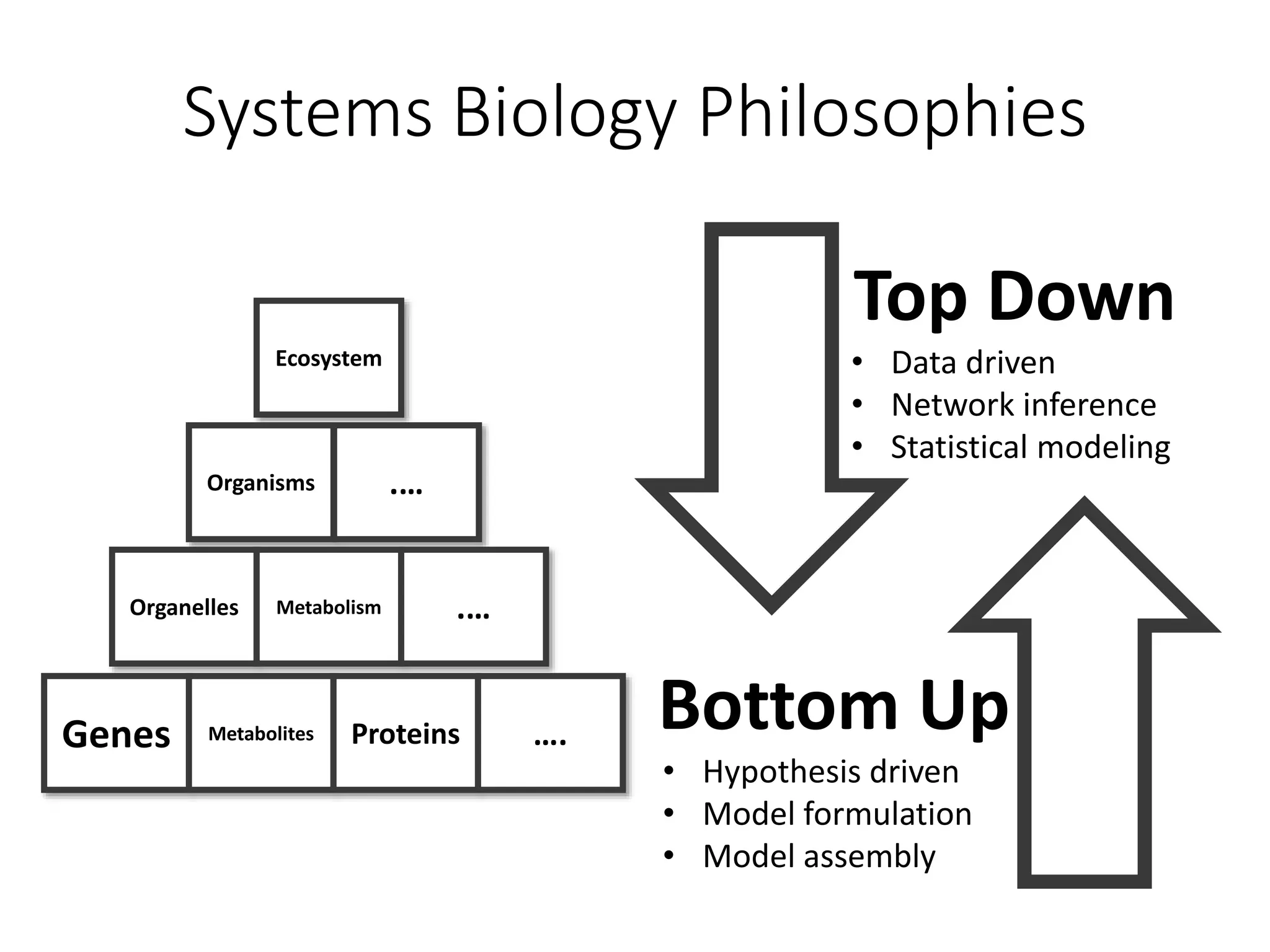
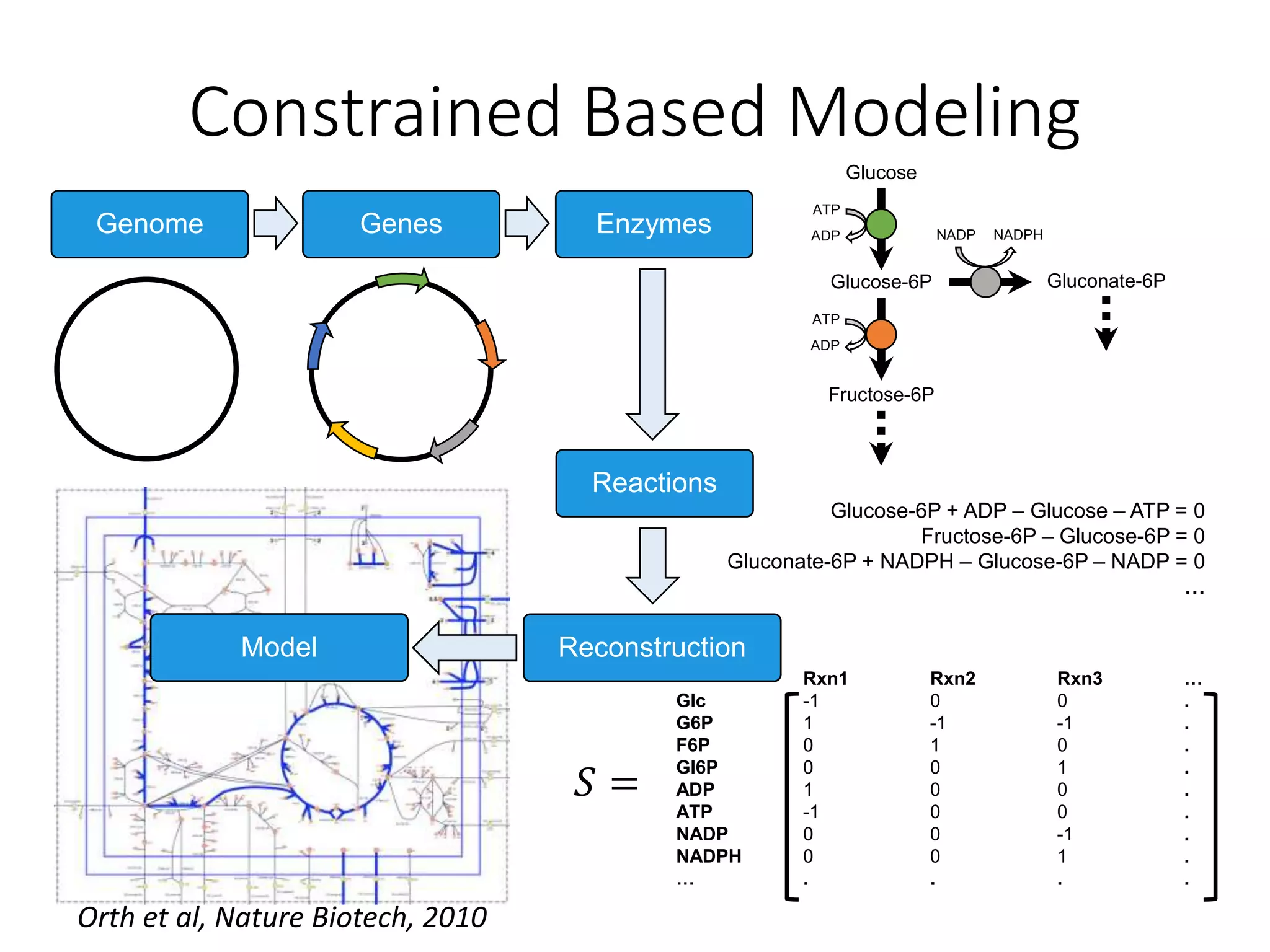
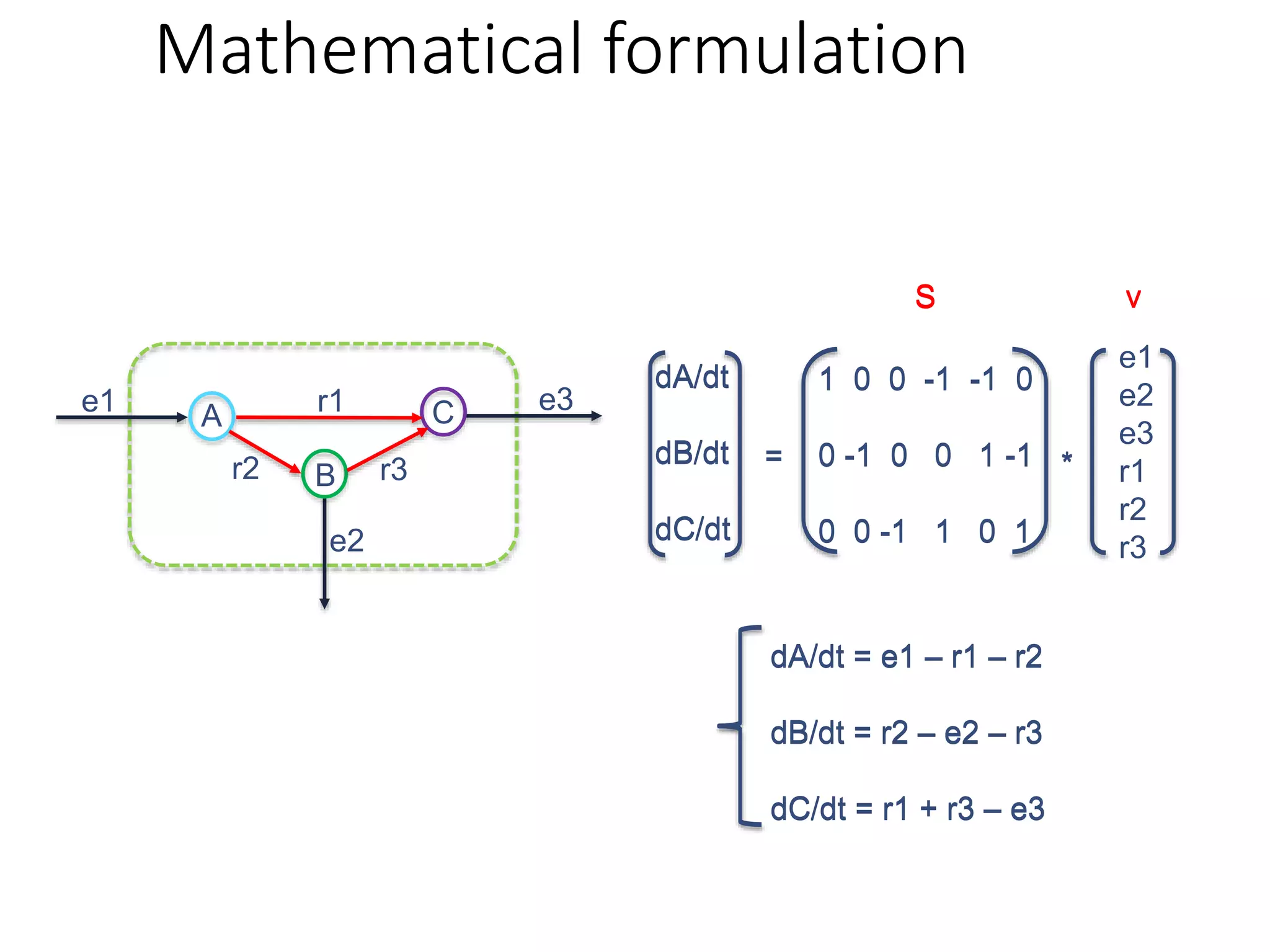
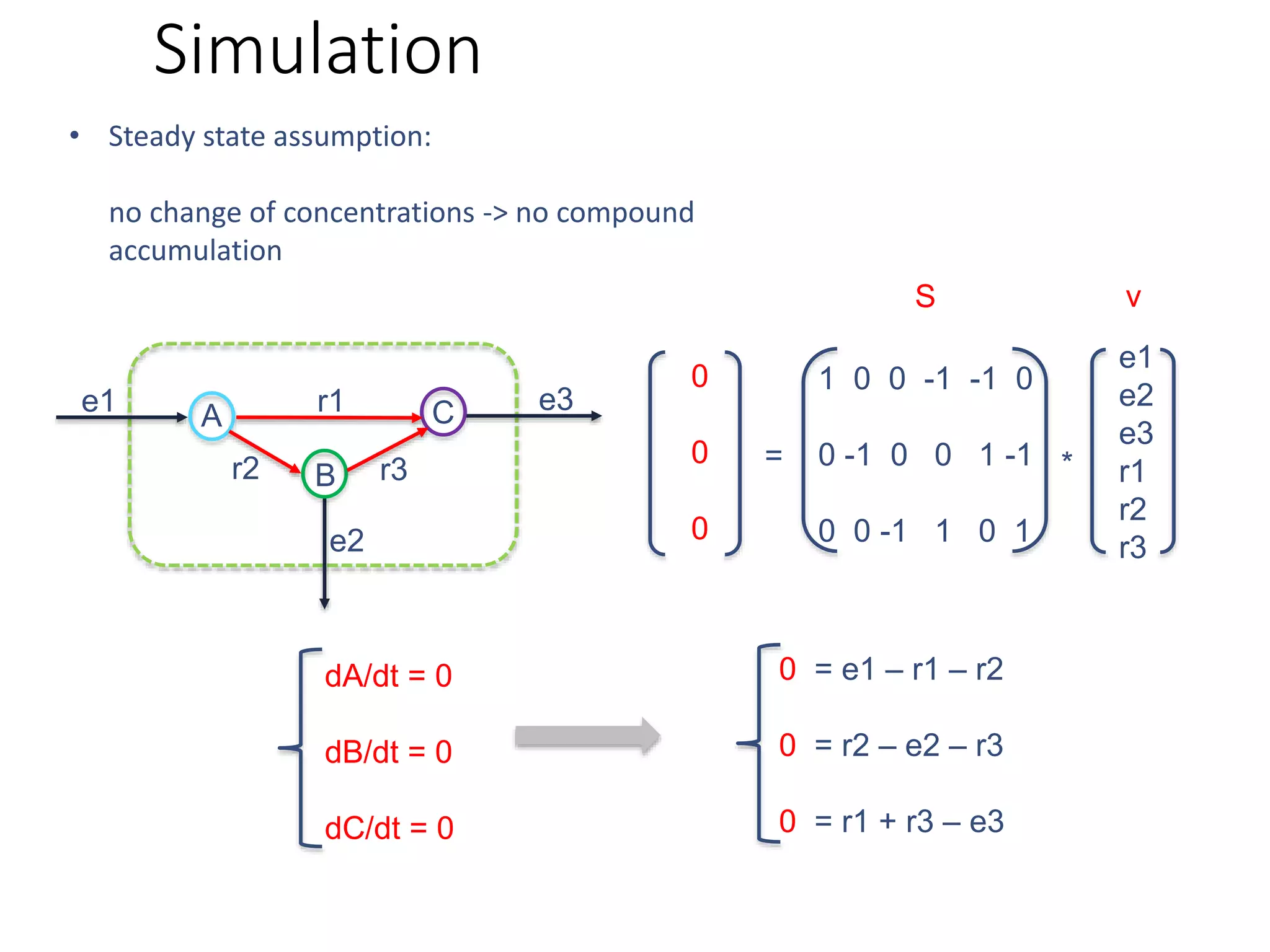
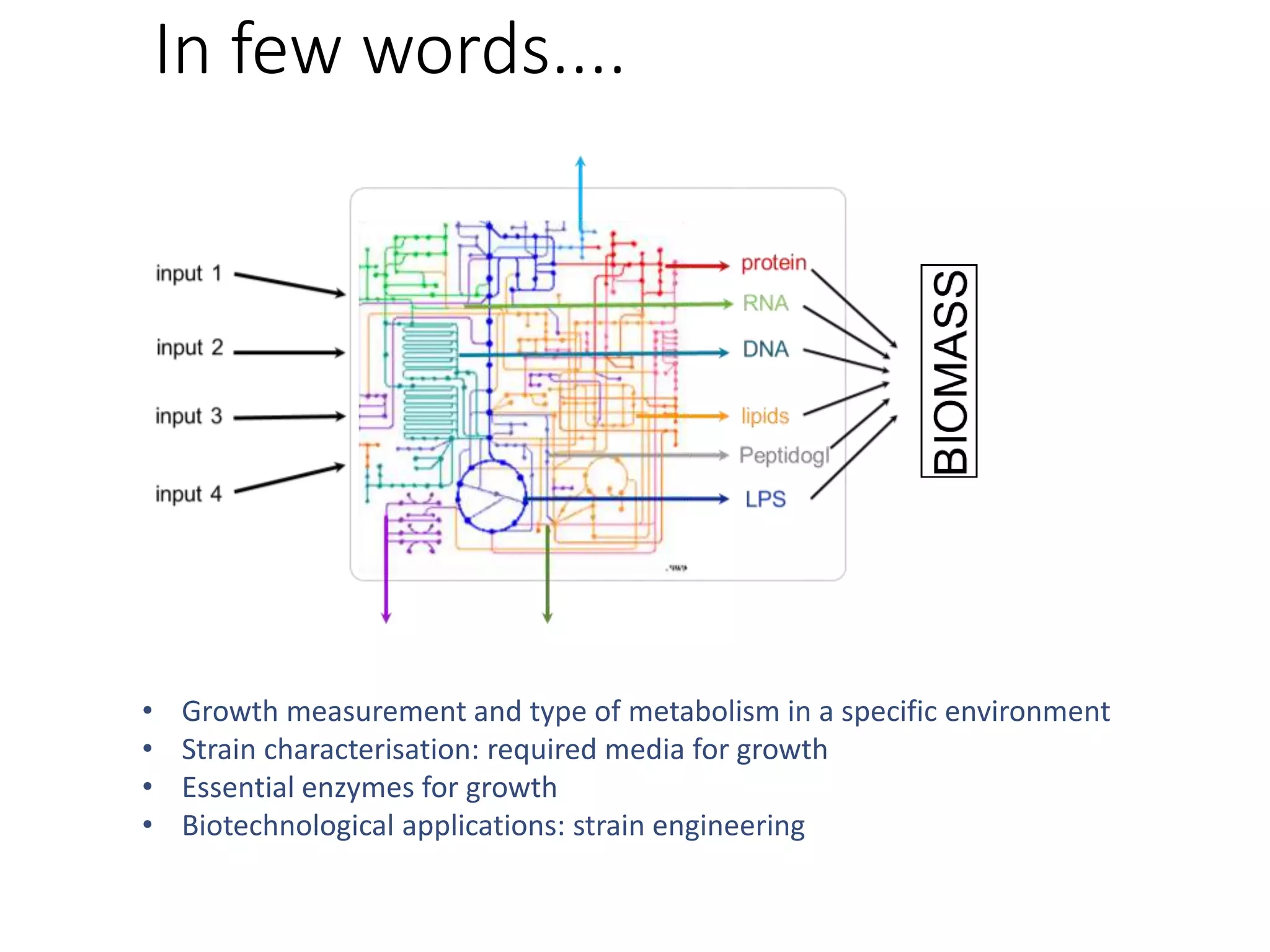
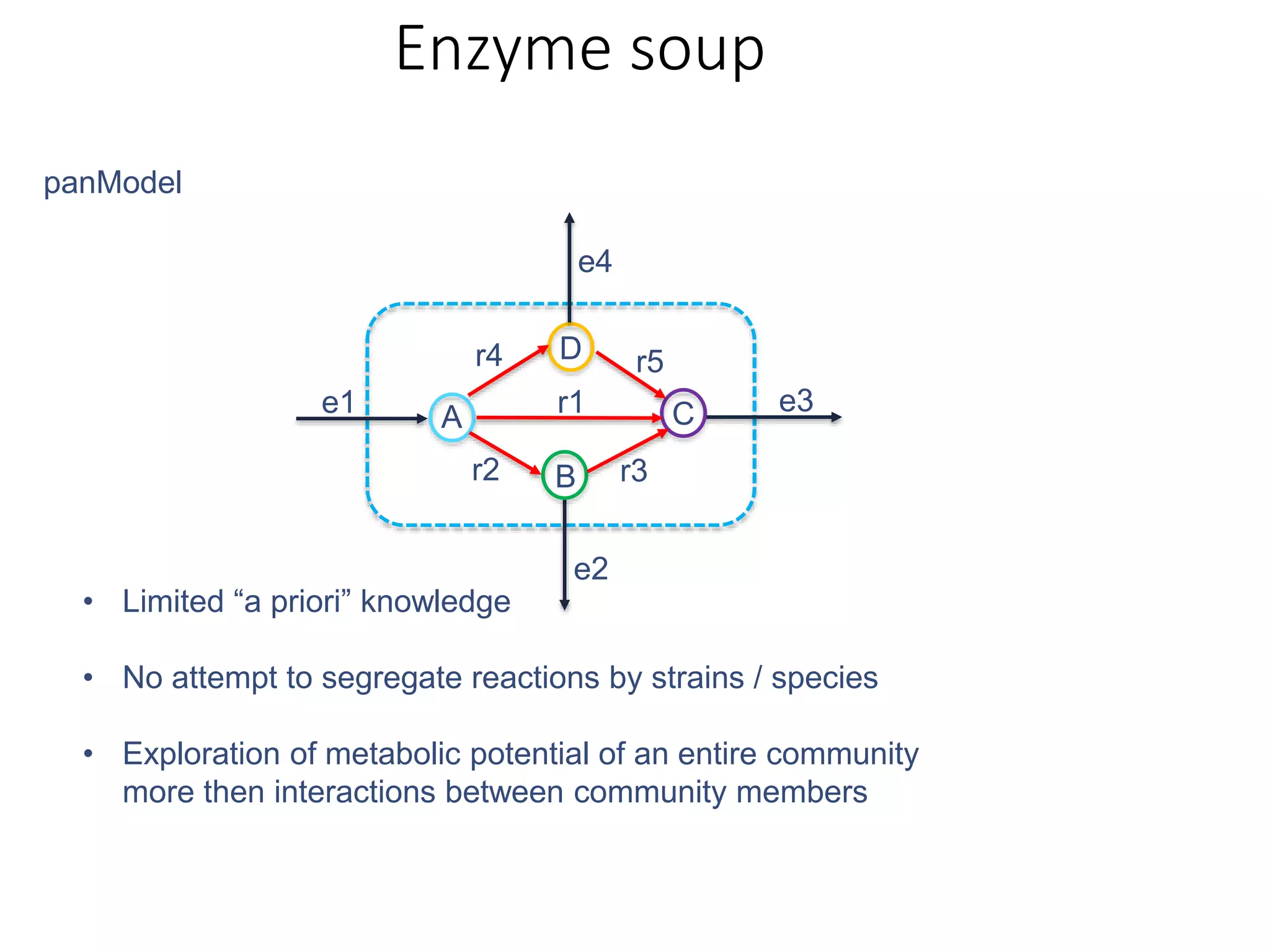
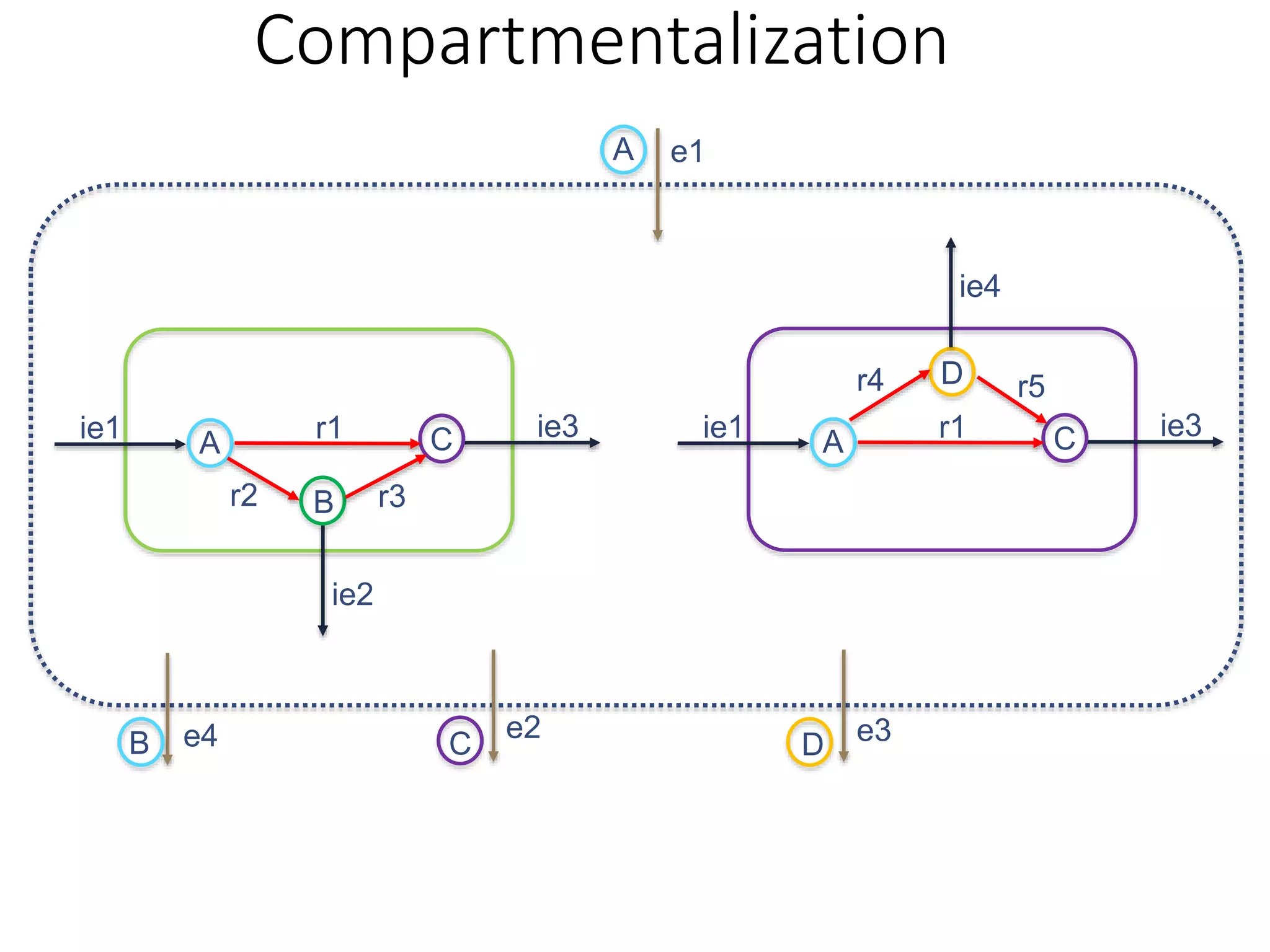
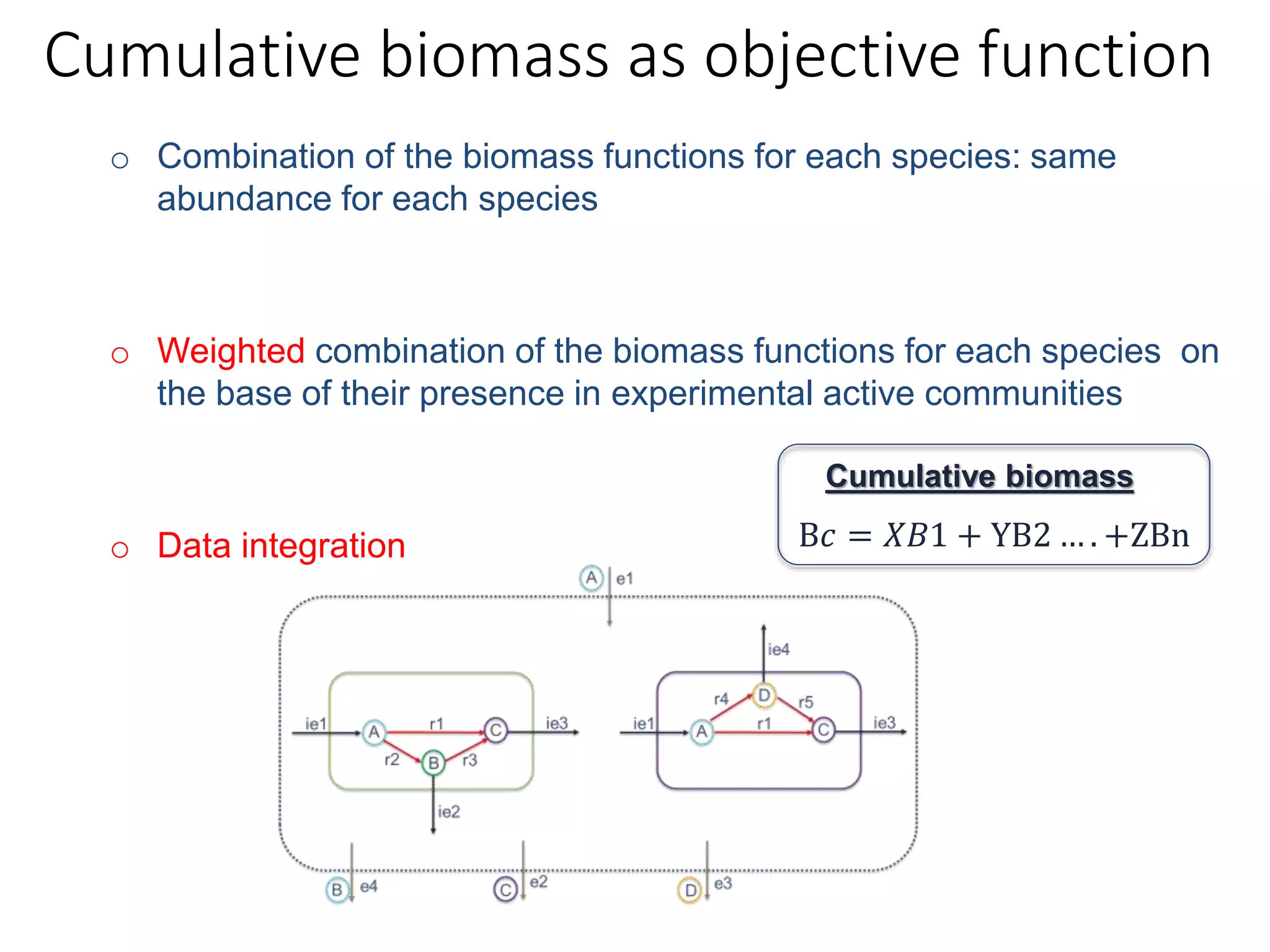
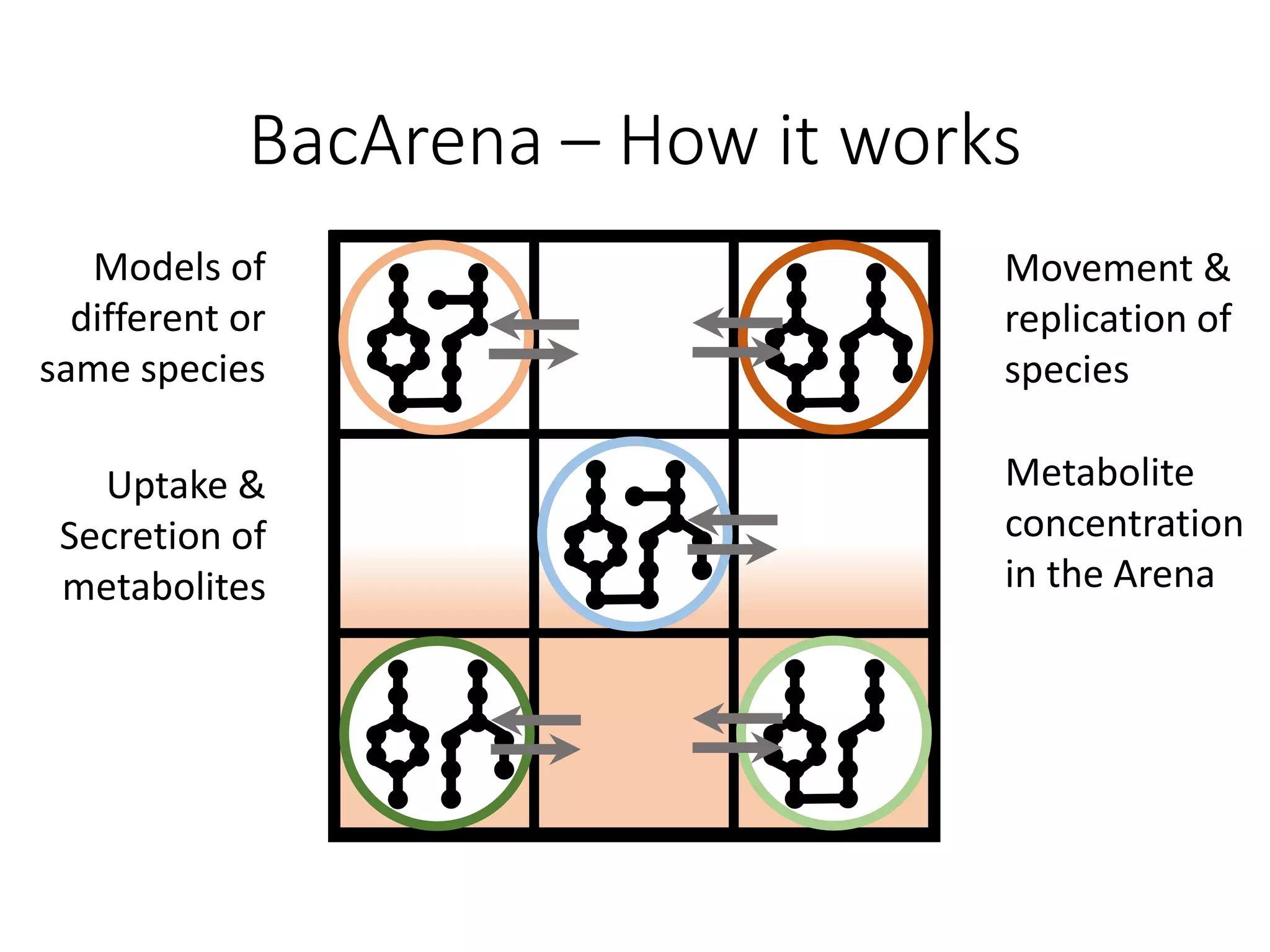
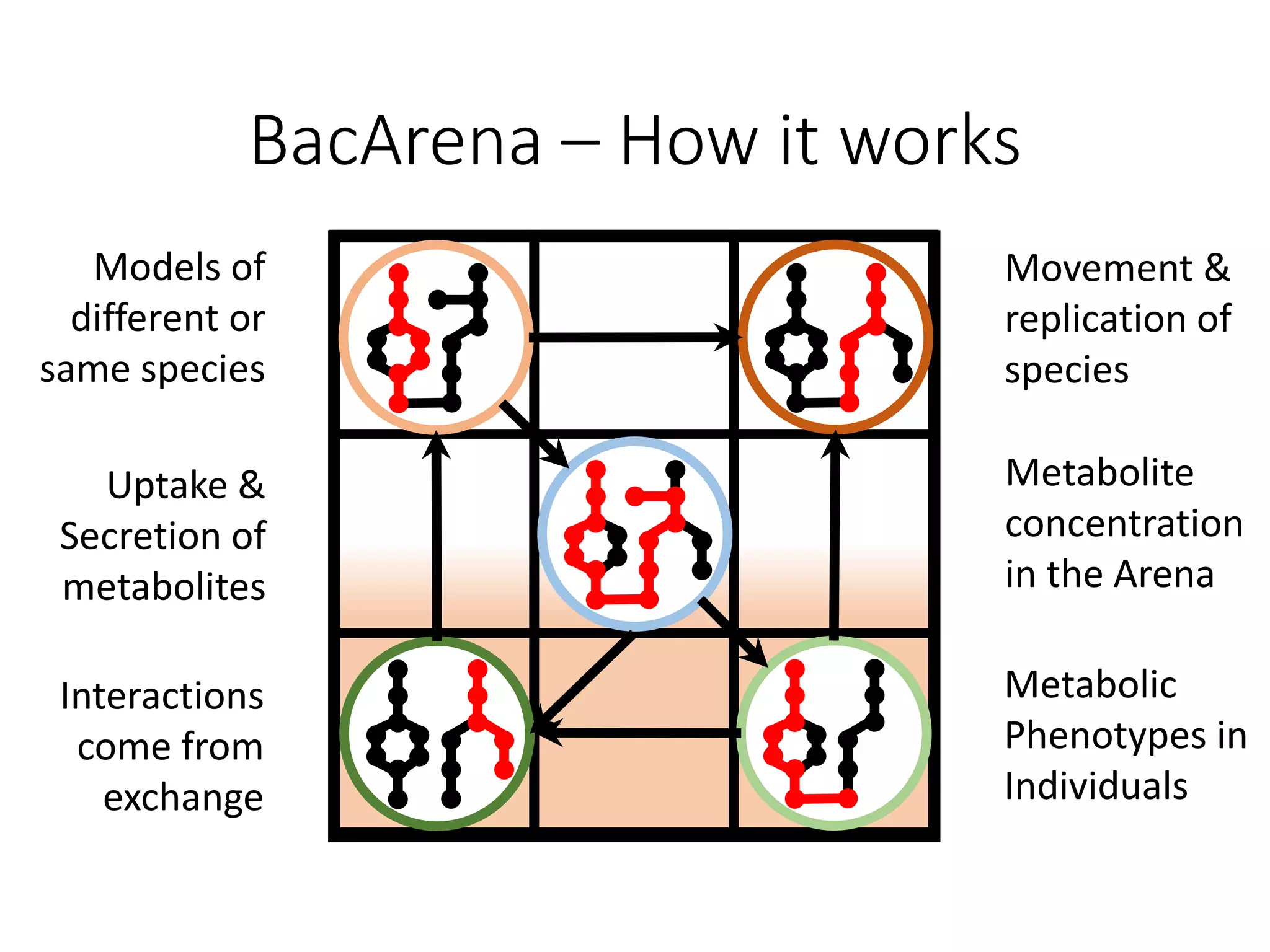
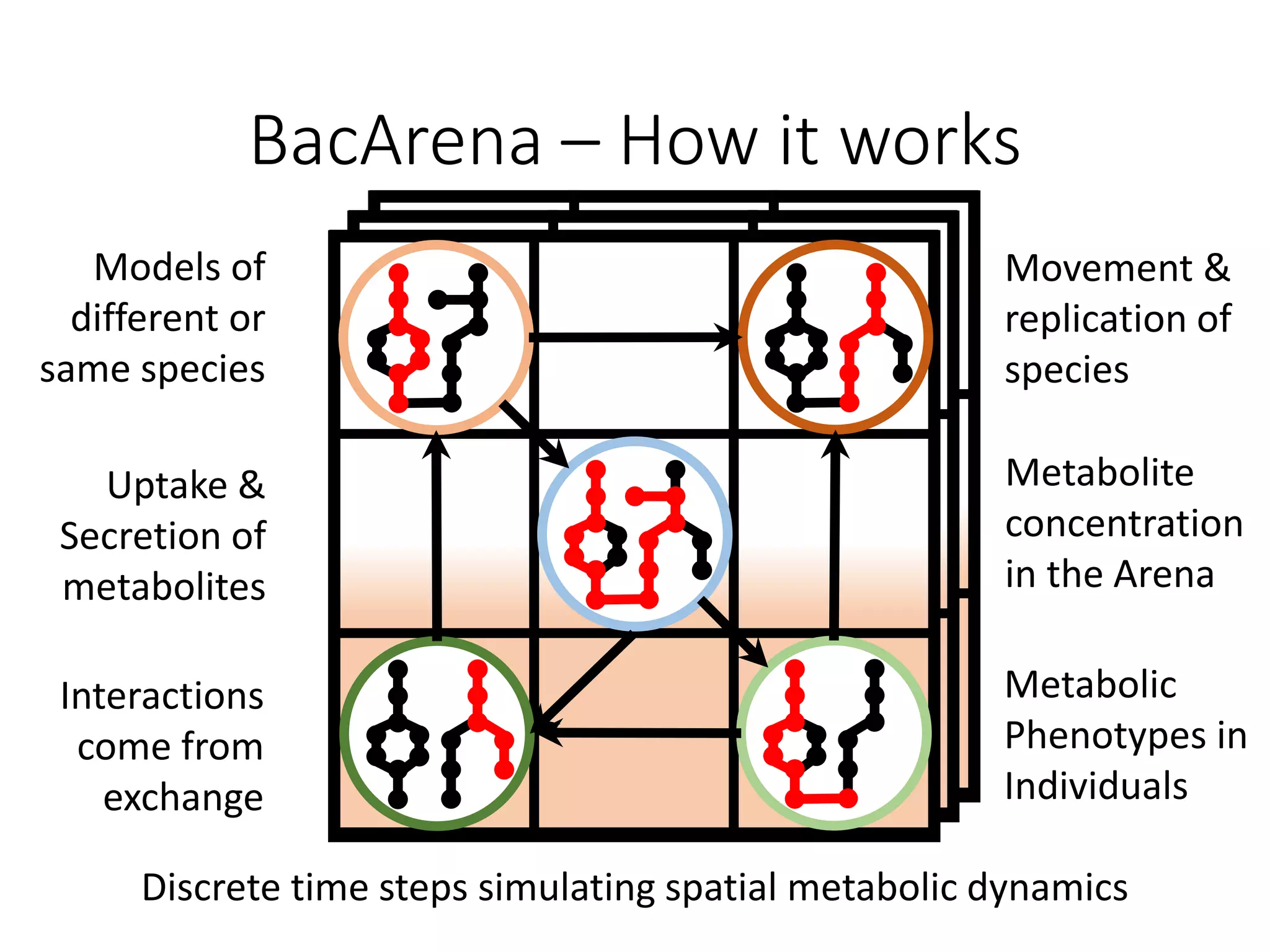
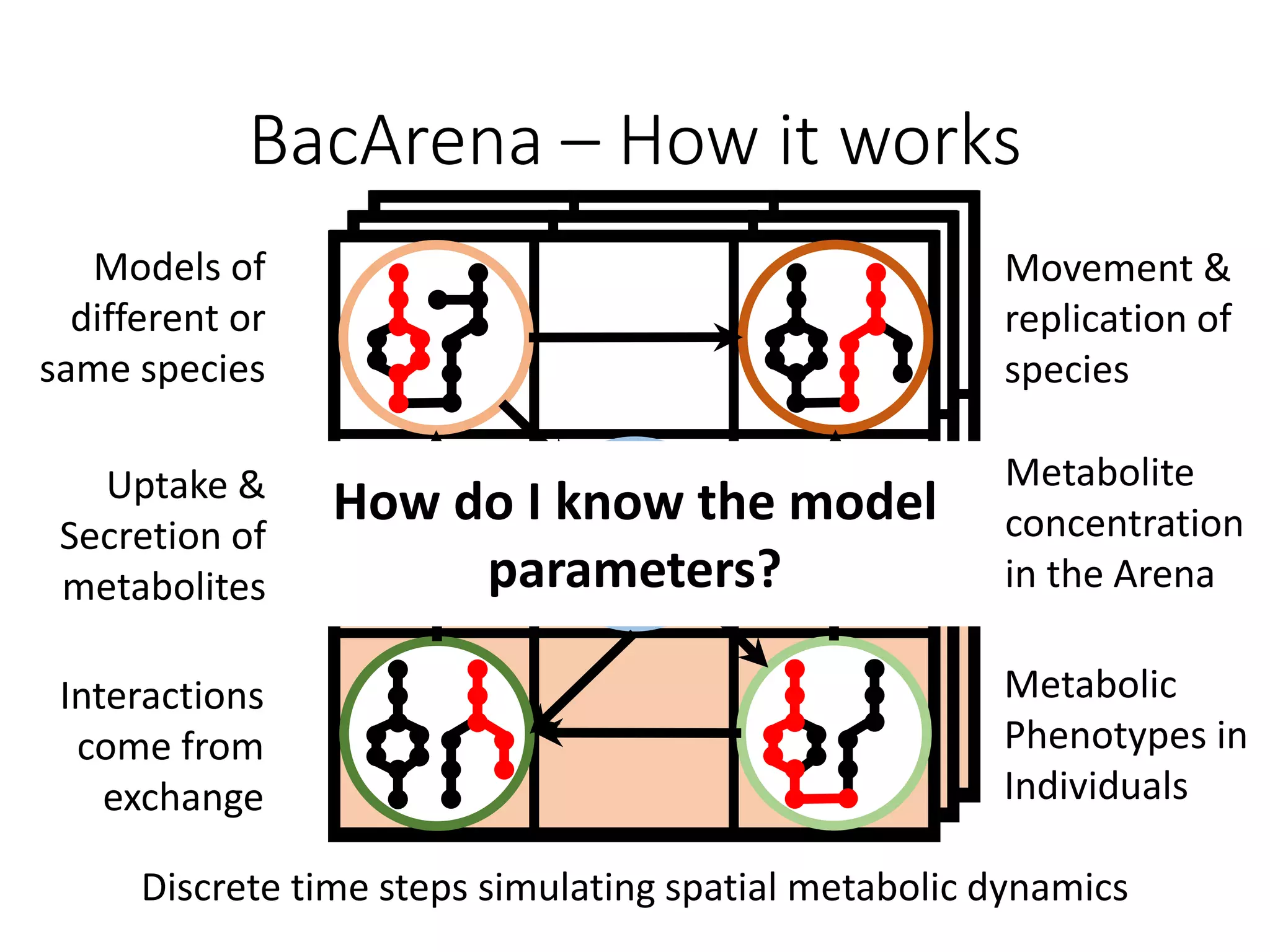
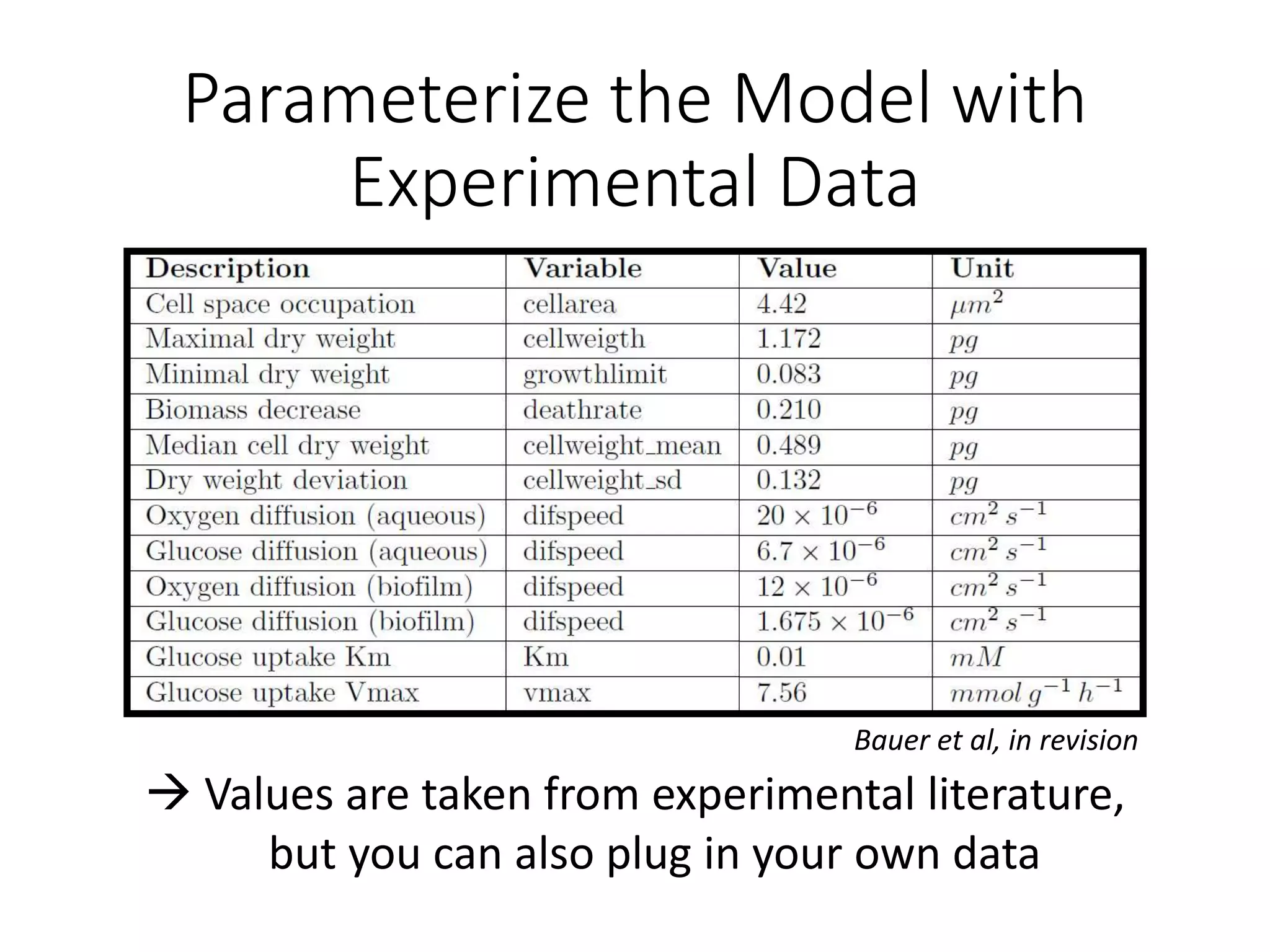
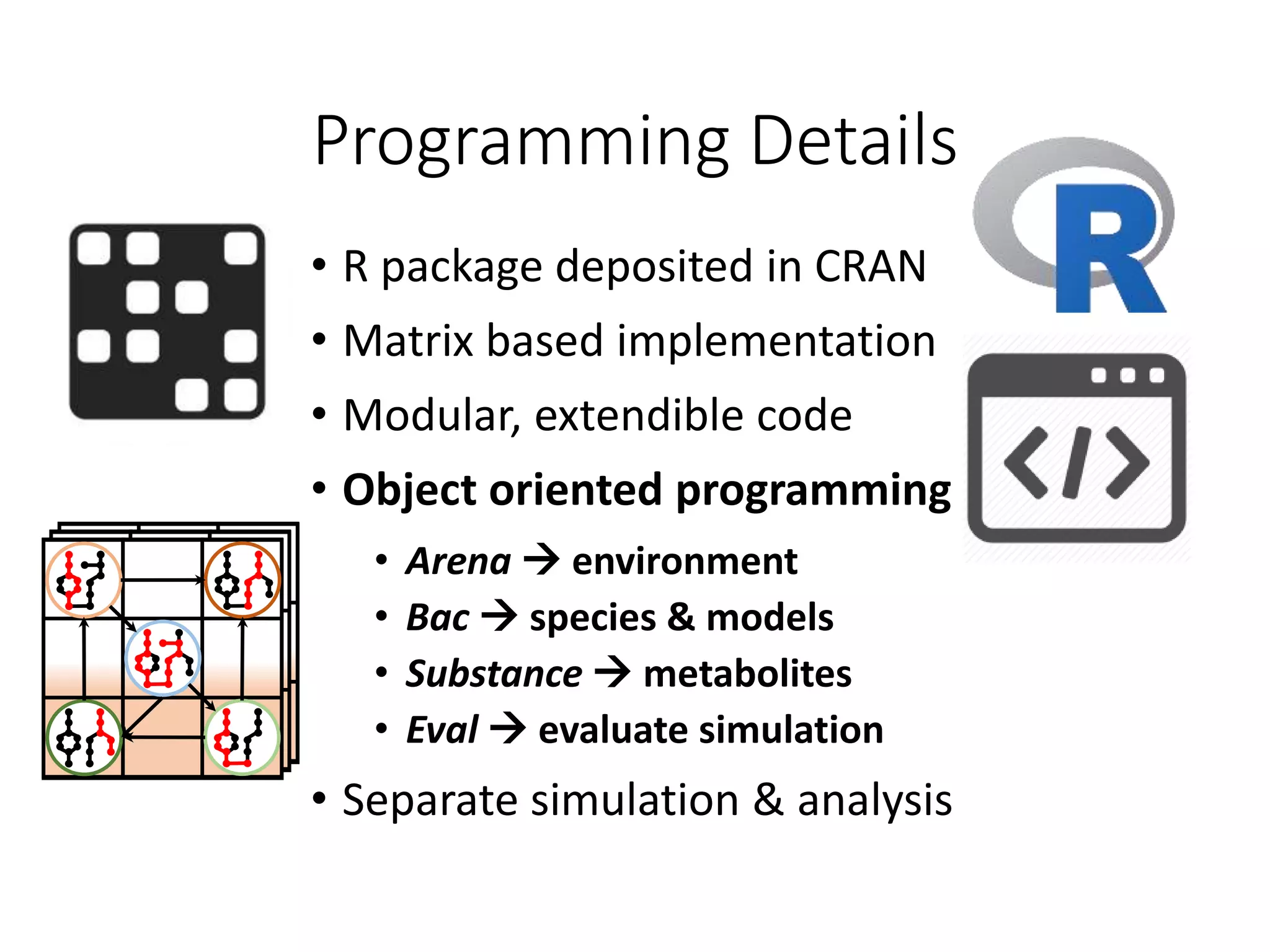
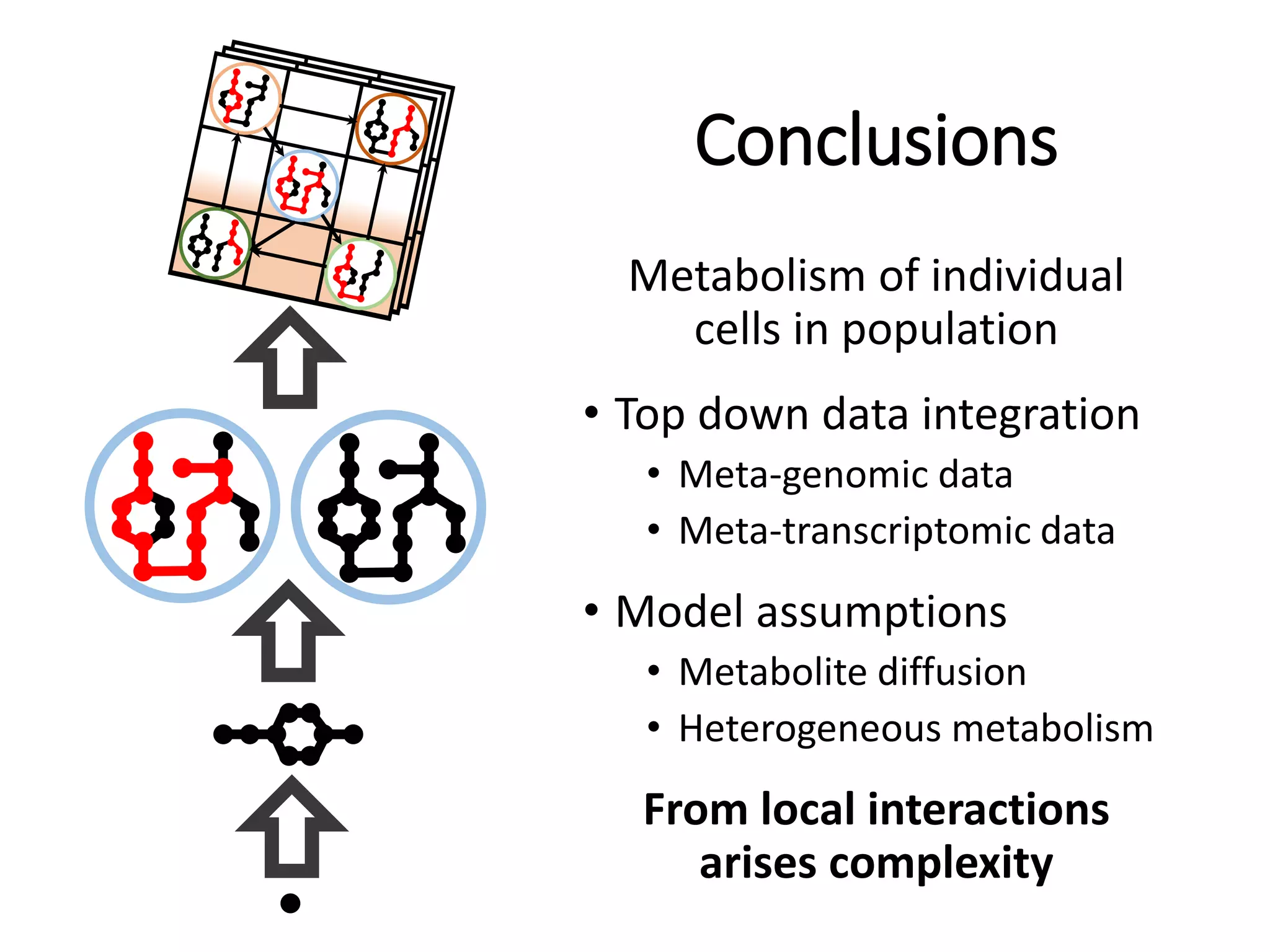
The document outlines a workshop on community modeling led by Federico Baldini and Eugen Bauer, focusing on systems biology and the significance of interactions among biological components. It introduces a tool named Bacarena for simulating metabolic dynamics within microbial communities, employing both constrained and agent-based models. The workshop includes discussions on theoretical frameworks, practical applications, and programming details for model implementation.

1. Community Modeling
Workshop
Federico Baldini & Eugen Bauer

2. What are we going to do today?
1. Motivation – Eugen
2. Introduction – Federico
3. Theory of BacArena – Eugen
4. BacArena practical – Eugen
5. Social event – Susanne

3. Why I study Science

4. Jeong et al, Nature, 2011
Why I study Systems Biology
Emergence: Phenomenon in which
larger components arise through local
interactions of smaller components such
that larger components have additional
properties
Systems biology: Study of the
interactions between the components of
biological systems, and how these
interactions give rise to the function of
that system

5. Systems Biology Philosophies
Top Down
• Data driven
• Network inference
• Statistical modeling
Bottom Up
• Hypothesis driven
• Model formulation
• Model assembly
Genes Metabolites Proteins ….
Organelles Metabolism .…
Organisms .…
Ecosystem

6. Systems Biology Philosophies
Top Down
• Data driven
• Network inference
• Statistical modeling
Bottom Up
• Hypothesis driven
• Model formulation
• Model assembly
Genes Metabolites Proteins ….
Organelles Metabolism .…
Organisms .…
Ecosystem

7. Genome GenomeGenes Enzymes
Glucose
Glucose-6P
Fructose-6P
Gluconate-6P
ATP
ADP
ATP
ADP
NADP NADPH
Constrained Based Modeling

8. Glucose-6P + ADP – Glucose – ATP = 0
Fructose-6P – Glucose-6P = 0
Gluconate-6P + NADPH – Glucose-6P – NADP = 0
…
Genome GenomeGenes Enzymes
Reactions
Reconstruction
Glucose
Glucose-6P
Fructose-6P
Gluconate-6P
ATP
ADP
ATP
ADP
NADP NADPH
Rxn1 Rxn2 Rxn3 …
Glc -1 0 0 .
G6P 1 -1 -1 .
F6P 0 1 0 .
Gl6P 0 0 1 .
ADP 1 0 0 .
ATP -1 0 0 .
NADP 0 0 -1 .
NADPH 0 0 1 .
… . . . .
𝑆 =
Model
Orth et al, Nature Biotech, 2010
Constrained Based Modeling

9. Now it’s Federicos turn

10. Mathematical formulation
A
B
Cr1
r2 r3
e1
e2
e3

11. Mathematical formulation
dA/dt
dB/dt
dC/dt
e1
e2
e3
r1
r2
r3
1 0 0 -1 -1 0
0 -1 0 0 1 -1
0 0 -1 1 0 1
= *
S v
dA/dt = e1 – r1 – r2
dB/dt = r2 – e2 – r3
dC/dt = r1 + r3 – e3
dA/dt
dB/dt
dC/dt
1 0 0 -1 -1 0
0 -1 0 0 1 -1
0 0 -1 1 0 1
= *
S v
dA/dt = e1 – r1 – r2
dB/dt = r2 – e2 – r3
dC/dt = r1 + r3 – e3
A
B
Cr1
r2 r3
e1
e2
e3

12. Simulation
• Steady state assumption:
no change of concentrations -> no compound
accumulation
0
0
0
e1
e2
e3
r1
r2
r3
1 0 0 -1 -1 0
0 -1 0 0 1 -1
0 0 -1 1 0 1
= *
S v
0 = e1 – r1 – r2
0 = r2 – e2 – r3
0 = r1 + r3 – e3
dA/dt = 0
dB/dt = 0
dC/dt = 0
A
B
Cr1
r2 r3
e1
e2
e3

13. A
B
Cr1
r2 r3
e1
e2
e3
1 0 0 -1 -1 0
0 -1 0 0 1 -1
0 0 -1 1 0 1
= *
S v
• Steady state assumption
• Constrained flux assumption
0
0
0
0 = e1 – r1 – r2
0 = r2 – e2 – r3
0 = r1 + r3 – e3
e1
e2
e3
r1
r2
r3
Simulation

14. Simulation: Flux Balance Analysis
e1
e2
e3
r1
r2
r3
1 0 0 -1 -1 0
0 -1 0 0 1 -1
0 0 -1 1 0 1
= *
S v
• Steady state assumption
• Constrained flux assumption
• Objective function (biomass) optimization
0 = e1 – r1 – r2
0 = r2 – e2 – r3
0 = r1 + r3 – e3
0
0
0

15. In few words....
• Growth measurement and type of metabolism in a specific environment
• Strain characterisation: required media for growth
• Essential enzymes for growth
• Biotechnological applications: strain engineering

16. Examples of applications

17. Examples of applications

18. Biofilm Gut microbiota
http://ausubellab.mgh.harvard.edu/picturehtml/pic20.html
Zoetendal, Raes et al. (2012)
Pseudomonas aeruginosa biofilm
Biofilm microcolony formed by P. aeruginosa strain PA14
carrying GFP. Biofilms were cultivated in flow chambers under
continuous culture conditions. Analysis of biofilm spatial
structures were done using confocal scanning laser microscopy
after 9 hours of incubation.
From single organism to community modeling

19. Enzyme soup
A
B
Cr1
r2 r3
e1
e2
e3
Model 1

20. A Cr1e1 e3
D
e4
r4 r5
Model 2
Enzyme soup

21. A
B
Cr1
r2 r3
e1
e2
e3
D
e4
r4 r5
panModel
• Limited “a priori” knowledge
• No attempt to segregate reactions by strains / species
• Exploration of metabolic potential of an entire community
more then interactions between community members
Enzyme soup

22. Compartmentalization
A
B
Cr1
r2 r3
e1
e2
e3 A Cr1e1 e3
D
e4
r4 r5

23. A
B
Cr1
r2 r3
ie1
ie2
ie3 A Cr1ie1 ie3
D
ie4
r4 r5
e1
e2 e3e4
A
B C D
Compartmentalization

24. Cumulative biomass as objective function
o Combination of the biomass functions for each species: same
abundance for each species
o Weighted combination of the biomass functions for each species on
the base of their presence in experimental active communities
o Data integration B𝑐 = 𝑋𝐵1 + YB2 … . +ZBn
Cumulative biomass

25. Simulating ecosystems: modeling bacteria communities
o Enzyme soup
Exploring community potential
No Individuals representation
o Compartmentalization
Abundances fixed and not changing
No concentrations
No time and space resolved simulation
Variable control problem
predict uptake and secretion of
metabolites with known species
abundances
predict community growth
with known uptake and secretion rates
o Agent Based modeling integration

26. Now it’s Eugens turn
What is BacArena?

27. BacArena = Bac + Arena

28. BacArena – How it works
Models of
different or
same species
Integration of constrained and agent based modeling

29. BacArena – How it works
Models of
different or
same species
Movement &
Replication of
species

30. BacArena – How it works
Models of
different or
same species
Movement &
Replication of
species
Metabolite
concentration
in the Arena

31. BacArena – How it works
Models of
different or
same species
Movement &
replication of
species
Metabolite
concentration
in the Arena
Uptake &
Secretion of
metabolites

32. BacArena – How it works
Models of
different or
same species
Movement &
replication of
species
Metabolite
concentration
in the Arena
Uptake &
Secretion of
metabolites
Interactions
come from
exchange

33. BacArena – How it works
Models of
different or
same species
Movement &
replication of
species
Metabolite
concentration
in the Arena
Uptake &
Secretion of
metabolites
Interactions
come from
exchange
Metabolic
Phenotypes in
Individuals

34. BacArena – How it works
Models of
different or
same species
Movement &
replication of
species
Metabolite
concentration
in the Arena
Uptake &
Secretion of
metabolites
Interactions
come from
exchange
Metabolic
Phenotypes in
Individuals
Discrete time steps simulating spatial metabolic dynamics

35. BacArena – How it works
Models of
different or
same species
Movement &
replication of
species
Metabolite
concentration
in the Arena
Uptake &
Secretion of
metabolites
Interactions
come from
exchange
Metabolic
Phenotypes in
Individuals
Discrete time steps simulating spatial metabolic dynamics
How do I know the model
parameters?

36. Parameterize the Model with
Experimental Data
Bauer et al, in revision
 Values are taken from experimental literature,
but you can also plug in your own data

37. Programming Details
• R package deposited in CRAN
• Matrix based implementation
• Modular, extendible code
• Object oriented programming
• Arena  environment
• Bac  species & models
• Substance  metabolites
• Eval  evaluate simulation
• Separate simulation & analysis

38. Programming Details
• R package deposited in CRAN
• Matrix based implementation
• Modular, extendible code
• Object oriented programming
• Arena  environment
• Bac  species & models
• Substance  metabolites
• Eval  evaluate simulation
• Separate simulation & analysis

39. Programming Details
• R package deposited in CRAN
• Matrix based implementation
• Modular, extendible code
• Object oriented programming
• Arena  environment
• Bac  species & models
• Substance  metabolites
• Eval  evaluate simulation
• Separate simulation & analysis

40. Programming Details
• R package deposited in CRAN
• Matrix based implementation
• Modular, extendible code
• Object oriented programming
• Arena  environment
• Bac  species & models
• Substance  metabolites
• Eval  evaluate simulation
• Separate simulation & analysis

41. Programming Details
• R package deposited in CRAN
• Matrix based implementation
• Modular, extendible code
• Object oriented programming
• Arena  environment
• Bac  species & models
• Substance  metabolites
• Eval  evaluate simulation
• Separate simulation & analysis

42. Now let’s start the
Demonstration
Everything will be uploaded here:
http://rsg-luxembourg.iscbsc.org/

43. Availability of BacArena
• Paper is currently under revision
• Official version is on CRAN:
• https://CRAN.R-project.org/package=BacArena
• Development version is hosted on GitHub:
• https://github.com/euba/BacArena

44. Compare with Experiments
Photomicrograph
of P. aeruginosa
biofilm cross
sections stained
for APase activity
Xu et al, Appl Environ Microbiol, 1998

45. Conclusions
Metabolism of individual
cells in population
• Top down data integration
• Meta-genomic data
• Meta-transcriptomic data
• Model assumptions
• Metabolite diffusion
• Heterogeneous metabolism
From local interactions
arises complexity

46. Acknowledgments
Molecular Systems
Physiology Group:
Ines Thiele (PI)
Stefania Magnusdottir
Marouen Guebilla
Dmitry Ravcheev
Laurent Heirendt
Alberto Noronha
Federico Baldini
Almut Heinken
Maike Aurich
Christian-Albrechts-Universität Kiel:
Christoph Kaleta
Johannes Zimmermann
Thanks to the HPC facilities of the University of Luxembourg

47. The RSG Luxembourg Board
… the RSG spirit

48. More RSG Courses – Stay Tuned!
20.03. B'RAIN Company Presentation
When? Monday 20.03.2017 from 17:00 to 19:00
Where? Maison du Savoir Room 4.410
05.04. Latex Workshop
When? Monday 05.04.2017 from 17:00 to 19:00
Where? Maison du Savoir Room 4.410
12.04. Git Workshop
When? Wednesday 12.04.2017 from 17:00 to 19:00
Where? TBA

49. Further Acknowledgments
Join us as a RSG Luxembourg member!
Thank you for attention

50. THE END