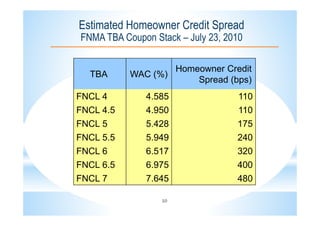
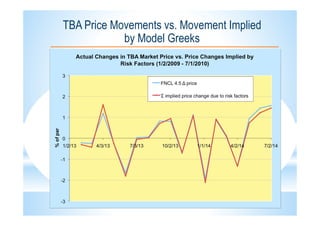
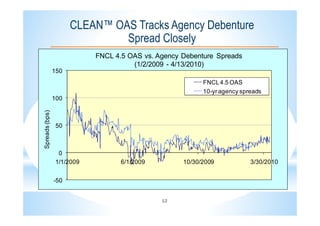
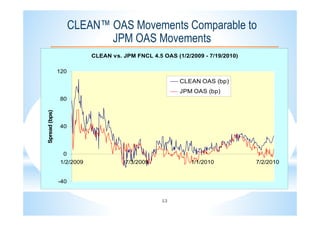
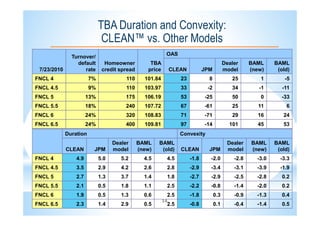
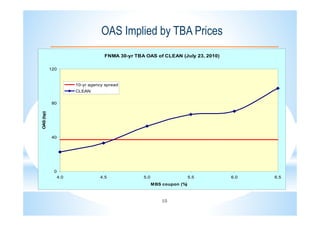
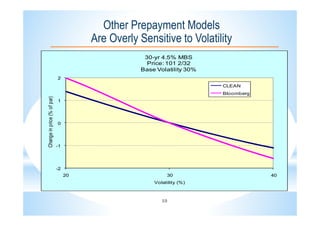
This document describes the CLEANTM model for valuing mortgage-backed securities (MBS). The CLEANTM model treats mortgages as callable amortizing bonds and models prepayments by dividing mortgage pools into buckets based on borrower behavior. The key risk factors in the model are interest rates, volatility, and homeowner credit spreads. The model calibrates quickly and intuitively based on observable market data. It provides realistic valuations, risk measurements, and trading opportunities without the limitations of other prepayment models.

1. 61 Broadway New York, NY 10006 212.482.0900 www.kalotay.com
CLEAN™: A Risk-Neutral
Approach to MBS Valuation

2. 2
What Is an Ideal MBS Valuation Model?
MBS price driven by parsimonious set of risk factors
Each factor is readily observed and measured
Risk factor values and sensitivities match reality
Leads to trading opportunities
Unhedged risk factors signal rich/cheap opportunities
Provides a robust basis for risk management
Probability distributions for risk factors imply probability distribution for the
MBS price

3. 3
Other Desirable Features
Minimal dependence on historical econometric data
No redesign required when market conditions change
Speed: fast calibration and valuation

4. 4
Initial Observations
Modeling prepayments is only a means to an end
The real goal is proper valuation and risk measurement
A mortgage is a callable amortizing bond
Prepayment models should be consistent with callable bond models
Bonds (mortgages) are called (refinanced) when the call (refinancing)
option is worth more dead than alive
Bond and MBS models should therefore respond similarly to changes in
interest rate levels and volatilities

5. 5
The CLEAN™ Way
Modeling prepayments
Turnover and defaults modeled using deterministic speeds
Refinancings modeled using stochastic interest rate model
Modeling a mortgage
As a callable amortizing bond
A financial engineer will refinance when the option is worth more dead than
alive
Others will refinance too early (never really happens) or too late
(“laggards”)
Modeling heterogeneous refinancing behavior
Divide mortgage pool into 10 buckets according to laggard parameter
Use a standard laggard distribution for a new pool
Modeling seasoned pools
Fastest refinancing buckets disappear first
Automatically accounts for ‘burnout’

6. 6
Risk Factors in the CLEAN™ MBS Model
Interest rate
USD swap curve
Swaption volatilities
Prepayment
Laggard distribution
Turnover speed
Default/buyout speed and recovery percentage
Refinancing cost
Homeowner credit spread
OAS (option-adjusted spread to swap curve)

7. 7
Calibration of CLEAN™:
Straightforward and Intuitive
Rarely adjusted
Laggard distribution
Default recovery percentage
Refinancing cost
Occasionally adjusted
Turnover speed
Default/buyout speed
Adjusted monthly
Homeowner credit spread

8. 8
CLEAN Uses Two Separate Credit Spreads
Homeowner credit spread
Specifies the homeowner’s borrowing curve
Determines when homeowner would refinance
Refinance if refinancing option is worth more dead than alive
OAS
Spread demanded by MBS investor
Used for discounting MBS cash flows
Reflects
Credit spread of guarantor
Plus market discount for unhedged uncertainty in price

9. 9
Homeowner Credit Spread:
Key Driver of Refinancing Speed
For current coupon pool
Conceptually the spread between a “par mortgage curve” and swap curve
Current primary mortgage rate minus volatility minus 10y swap rate
Implies refi option premium of approximately 40 bps
Comparable to single-A/BBB 10-year corporate credit
For higher coupon pool
Wider than current coupon spread due to credit impairment
Start with current coupon homeowner credit spread
Add difference between WAC minus primary mortgage rate
Fine-tune by matching duration and convexity to dealer consensus

10. 10
Estimated Homeowner Credit Spread
FNMA TBA Coupon Stack – July 23, 2010
TBA WAC (%)
Homeowner Credit
Spread (bps)
FNCL 4 4.585 110
FNCL 4.5 4.950 110
FNCL 5 5.428 175
FNCL 5.5 5.949 240
FNCL 6 6.517 320
FNCL 6.5 6.975 400
FNCL 7 7.645 480

11. 11
TBA Price Movements vs. Movement Implied
by Model Greeks

12. 12
CLEAN™ OAS Tracks Agency Debenture
Spread Closely
-50
0
50
100
150
1/1/2009 6/1/2009 10/30/2009 3/30/2010
Spreads(bps)
FNCL 4.5 OAS vs. Agency Debenture Spreads
(1/2/2009 - 4/13/2010)
FNCL4.5 OAS
10-yragency spreads

13. 13
CLEAN™ OAS Movements Comparable to
JPM OAS Movements
CLEAN vs. JPM FNCL 4.5 OAS (1/2/2009 - 7/19/2010)
-40
0
40
80
120
1/2/2009 7/3/2009 1/1/2010 7/2/2010
Spread(bps)
CLEAN OAS (bp)
JPM OAS (bp)

14. 14
TBA Duration and Convexity:
CLEAN™ vs. Other Models
7/23/2010
Turnover/
default
rate
Homeowner
credit spread
TBA
price
OAS
CLEAN JPM
Dealer
model
BAML
(new)
BAML
(old)
FNCL 4 7% 110 101.84 23 8 25 1 -5
FNCL 4.5 9% 110 103.97 33 -2 34 -1 -11
FNCL 5 13% 175 106.19 53 -25 50 0 -33
FNCL 5.5 18% 240 107.72 67 -61 25 11 6
FNCL 6 24% 320 108.83 71 -71 29 16 24
FNCL 6.5 24% 400 109.81 97 -14 101 45 53
Duration Convexity
CLEAN JPM
Dealer
model
BAML
(new)
BAML
(old) CLEAN JPM
Dealer
model
BAML
(new)
BAML
(old)
FNCL 4 4.9 5.0 5.2 4.5 4.5 -1.8 -2.0 -2.8 -3.0 -3.3
FNCL 4.5 3.5 2.9 4.2 2.6 2.8 -2.9 -3.4 -3.1 -3.9 -1.9
FNCL 5 2.7 1.3 3.7 1.4 1.8 -2.7 -2.9 -2.5 -2.8 0.2
FNCL 5.5 2.1 0.5 1.8 1.1 2.5 -2.2 -0.8 -1.4 -2.0 0.2
FNCL 6 1.9 0.5 1.3 0.6 2.5 -1.8 0.3 -0.9 -1.3 0.4
FNCL 6.5 2.3 1.4 2.9 0.5 2.5 -0.8 0.1 -0.4 -1.4 0.5

15. 15
OAS Implied by TBA Prices
FNMA 30-yr TBA OAS of CLEAN (July 23, 2010)
0
40
80
120
4.0 4.5 5.0 5.5 6.0 6.5
MBS coupon (%)
OAS(bp)
10-yr agency spread
CLEAN

16. 16
Why CLEAN™ Is Ideal for
Trading, Hedging, and Risk Management
Realistic transparent behavior
Based on well established financial and economic principles
Instead of ad hoc mathematical formulas and parameters
Consistent with valuation models for callable bonds and
cancelable swaps
Calibration is straightforward and intuitive
Concretely defined model parameters
Easier to simulate
Model behavior always realistic
Based on fundamental financial and economic principles
Not on statistical fitting of historical behavior
And ridiculously fast
Critical for simulation

17. 17
Challenges Faced by Other Prepayment
Models But Not by CLEAN
Burnout
As pool ages, refinancing speed decreases
Model parameters are mathematical and not economic
Need to be estimated using fit to historical data
Rather than direct observation
Ongoing need to update not just parameters but the model itself
Estimating a future primary mortgage rate
Many models assume a fixed formula using spread to an interpolated
Treasury yield
But mortgage rate contains premium for refinancing option, which depends
on volatility
Computation speed
Use of Monte Carlo forces tradeoff between speed and precision

18. 18
Heard It Through The Grapevine
"The actual sensitivity of MSRs to implied volatility is complex and
somewhat controversial”
Ben Golub in “Mark-to-Market Methodology, Mortgage Servicing Rights,
and Hedging Effectiveness”
“The model we use doesn’t even get the sign right for volatility
hedging of MSRs”
A/L management advisor
“The price response to skew adjustment seems exaggerated”
Hedge fund manager
Why do intuition and model disagree
when it comes to volatility?

19. 19
Other Prepayment Models
Are Overly Sensitive to Volatility
-2
-1
0
1
2
20 30 40
Changeinprice(%ofpar)
Volatility (%)
30-yr 4.5% MBS
Price: 101 2/32
Base Volatility 30%
CLEAN
Bloomberg

20. 20
Why Other Prepayment Models
Struggle with Interest Rate Volatility
Others model future mortgage rate as a formula
Say a function of 2-yr and 10-yr Treasuries plus a fixed spread
Where fixed spread is refinancing option premium
Does not widen when volatility increases
So prepayments overreact to change in volatility
For example, if volatility increase
Option premium spread underestimated
Future mortgage rates underestimated
Refinancing speed overestimated
Higher-coupon MBS prices decline too much

21. 21
References
Andrew Kalotay & Qi Fu (June 2009), A Financial Analysis of
Consumer Mortgage Decisions, Mortgage Bankers Association.
Andrew Kalotay & Qi Fu (May 2008), Mortgage servicing rights and
interest rate volatility, Mortgage Risk.
Andrew Kalotay, Deane Yang, & Frank Fabozzi (Vol. 1, 2008), Optimum
refinancing: bringing professional discipline to household
finance, Applied Financial Economics Letters.
Andrew Kalotay, Deane Yang, & Frank Fabozzi (Vol. 3, 2007), Refunding
efficiency: a generalized approach, Applied Financial Economics
Letters.
Andrew Kalotay, Deane Yang, & Frank Fabozzi (December 2004), An
option-theoretic prepayment model for mortgages and
mortgage-backed securities, International Journal of Theoretical
and Applied Finance.
Available from http://www.kalotay.com/research