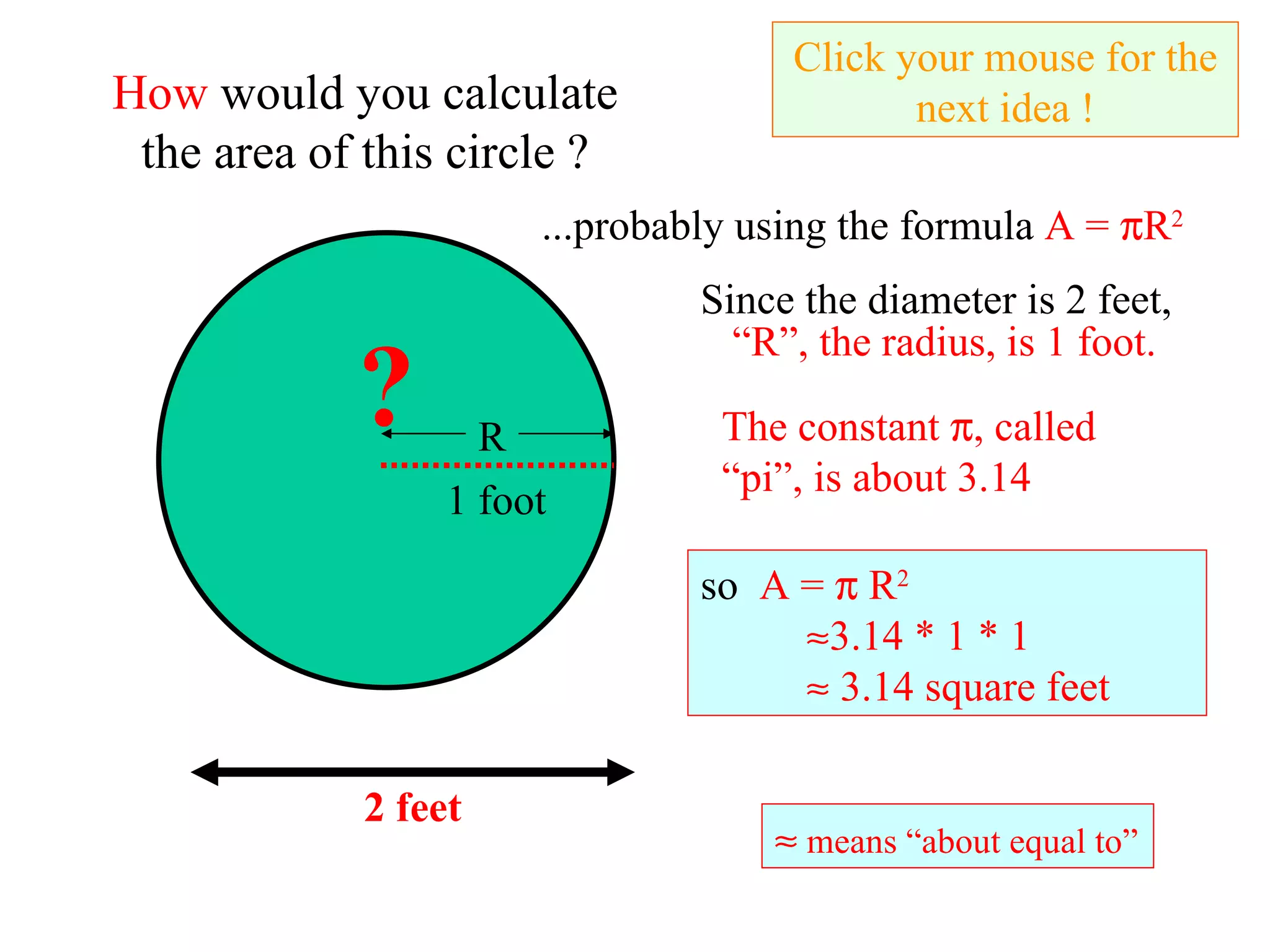
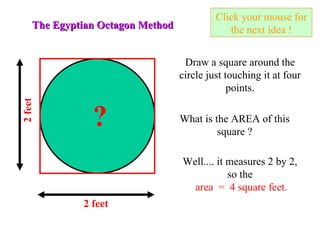
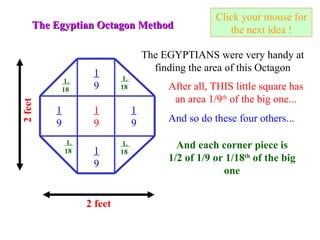
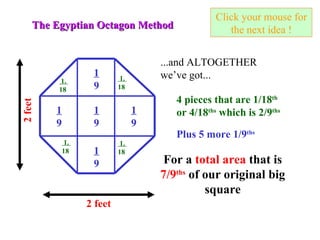
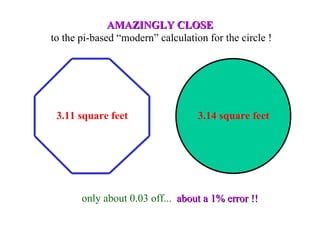
The document describes how to calculate the area of a circle with a diameter of 2 feet using the standard formula of A = πr^2 as well as an ancient Egyptian method. The Egyptian method involves drawing an octagon inside the circle and calculating its area, which approximates the area of the circle. It finds the octagon's area is 28/9 or 3 1/9 square feet, which is very close to the area calculated using pi.

1. How would you calculate the area of this circle ? ...probably using the formula A =  R 2 Since the diameter is 2 feet, Click your mouse for the next idea ! The constant  , called “pi”, is about 3.14 ? 2 feet so A =  R 2  3.14 * 1 * 1  3.14 square feet  means “about equal to” R 1 foot “ R”, the radius, is 1 foot.

2. Click your mouse for the next idea ! ? LETS explore how people figured out circle areas before all this  business ? The ancient Egyptians had a fascinating method that produces answers remarkably close to the formula using pi. 2 feet

3. Click your mouse for the next idea ! ? The Egyptian Octagon Method Draw a square around the circle just touching it at four points. What is the AREA of this square ? 2 feet Well.... it measures 2 by 2, so the area = 4 square feet. 2 feet

4. Click your mouse for the next idea ! The Egyptian Octagon Method 2 feet Now we divide the square into nine equal smaller squares. Sort of like a tic-tac-toe game ! Notice that each small square is 1/9 the area of the large one -- we’ll use that fact later ! 2 feet

5. Click your mouse for the next idea ! The Egyptian Octagon Method 2 feet Finally... we draw lines to divide the small squares in the corners in half, cutting them on their diagonals. Notice the 8-sided shape, an octagon, we have created ! Notice, also, that its area looks pretty close to that of our circle ! 2 feet

6. Click your mouse for the next idea ! The Egyptian Octagon Method 2 feet The EGYPTIANS were very handy at finding the area of this Octagon 2 feet 1 9 After all, THIS little square has an area 1/9 th of the big one... 1 9 1 9 1 9 1 9 And so do these four others... And each corner piece is 1/2 of 1/9 or 1/18 th of the big one 1. 18 1. 18 1. 18 1. 18

7. Click your mouse for the next idea ! The Egyptian Octagon Method 2 feet ...and ALTOGETHER we’ve got... For a total area that is 7/9 ths of our original big square 2 feet 1. 18 1. 18 1. 18 1. 18 4 pieces that are 1/18 th or 4/18 ths which is 2/9 ths 1 9 1 9 1 9 1 9 1 9 Plus 5 more 1/9 ths

8. Click your mouse for the next idea ! The Egyptian Octagon Method 2 feet FINALLY... Yep, we’re almost done ! The original square had an area of 4 square feet. So the OCTAGON’s area must be 7/9 x 4 or 28/9 or 3 and 1/9 or about 3.11 square feet 2 feet We have an OCTAGON with an area = 7/9 of the original square. 7 9

9. AMAZINGLY CLOSE to the pi-based “modern” calculation for the circle ! 3.11 square feet 3.14 square feet only about 0.03 off... about a 1% error !!