Chokudai Contest 001

©AtCoder Inc. All rights reserved. 1
Chokudai Contest 001
解説
AtCoder株式会社代表取締役
高橋直大

はじめに
• Writer（chokudai）が、約8時間のテストプレイで試せ
た方針のみ明記しています。
• もっと良い方針（89万点以上）は、Twitterのハッシュ
タグ#chokudai_1から見つけることが可能かもしれま
せん。そちらも併せてご確認ください。

問題概要
• N×Nのマスに、1～100の整数が書かれている。
• マスをなぞると、マスの中に書かれている整数が1
減る
– なぞる順は、中の整数が8,7,6,5…のように、1ずつ減って
いるようにしなければならない
– なぞれるマスは、今見ているマスの上下左右のみ
• なぞる回数を出来るだけ小さくしなさい
• 今回の問題ではN = 30

まずは点数を取ろう！
• 点数を取るには？
– 連鎖とか考えずにとりあえず0にすることだけ考えよう！
– 各マスについて、マスに書かれている整数分だけ座標を
出力する。
• これで、1～100で30*30マスあるとして、最大90000手
• 10万-手数がスコアなので、これで最低でも1ケース1万点
• 実際は平均50程度なので、45000手程度となり、5.5万点
– 10ケースあるのでおおよそ55万点が得られる。
2016/3/20 4

ちょっと工夫をしよう！
• 例えば、横に1個だけ繋げてみる
– 右の数が自分より1だけ小さかったら、そっちも減らす
• これだけでもスコアが結構あがる！
– それが出来たら、再帰処理をして、連続して減らす
• これだけでも物凄く上がる！
– これをちゃんと組むだけでも70万点くらい行きます。
• ちゃんと書いてないから自信ない
2016/3/20 5

その他の工夫
• スコアを減らすマスを選んでみよう！
– 大きい数から減らしていった方が良さそう？
• 例えば、こんな貪欲法がある
– 盤面の中から一番大きい整数を選ぶ。
– そこから上下左右を見て、繋げるところがあれば出来るだけ連鎖を
させることを繰り返す。
– これも80万点弱取れる。
– たくさん減らせるマスを採用するべき？
• こんな貪欲法もある
– とりあえず全部のマスから出来るだけ繋げてみる
– 一番長いものを採用する
– これを最後まで繰り返す。
– これも80万点弱くらい？
2016/3/20 6

ランダムを使おう！
• ここから、ランダムで色々変えてみる
– 色々試すと当然スコアも変わる！
• 選択するマスを変えてみる
• ルートを変えてみる
– 制限時間いっぱいまで試して、一番良いスコアを選ぶ
– これでもスコアは上がるが、そんなに上がらない
• もうちょっと賢い方法を考えよう！
2016/3/20 7

ランダムを使おう！
• ビームサーチや焼きなまし
– ビームサーチ
• 途中までの手番のうち、K番目に良いものを保持する
– 「良いもの」というのは、自分で適当な評価関数を作る
» 減らせてる数とか
» 各マスの減らされ具合の分布とか
» 隣り合う数の近さとか
» 孤立してるかとか
» もちろん全部入れる必要はない
• そのまま最後まで進めると、「ある程度良いものの候補」を保持して探索が出来る
ので、単純なランダムより良い
• 焼きなまし
– 前の解をちょっと変えて試す！
– 今回は使い辛そう？
• この辺を頑張ると多分85万くらいまでは行きます。
– ここから先は、もうちょっと問題の性質を掴まないと難しい＞＜
• 評価とか凄い頑張ると88万点台も出るっぽい・・・？
2016/3/20 8

補足
• ビームサーチや焼きなましにも限界が！
– 例えば、「54万点の出力の一部をランダムシャッフルした
後、シミュレートした答えを評価として焼きなましを行う」
• こんなんはまともなスコアが出ません
– ビームサーチや焼きなましを覚えることより、ちゃんと問
題の性質を掴むことの方が大切！
– 今回はこの辺りを使わなくても89万点は行けます。
2016/3/20 9

減らし方についての考察
• 一度消した列をひたすら減らし続けたりしそう。
– 例えば右図矢印のようにすると・・・？
• 赤い部分が孤立する！
• 孤立すると連鎖できなくなる！
– 逆に、横一線に減らすようにしてしまうと？
• 孤立点はなくなる
• 実は結構良い？
– でも適当なのでやっぱり大したことない
• どちらにしても「減らすパス」を意識しよう！
2016/3/20 10

「パス」を先に決める考え方
• 先に、「どういう順番で減らすか」を決めてしまうとど
うなるか？
– 例えば横一列が{7, 3, 6, 5, 3, 4, 1}だったとする。
– この1列を消すのに何手掛かるか？
• これは実は結構簡単に求まってしまう！
2016/3/20 11

• 横一列が{7, 3, 6, 5, 3, 4, 1}だったとする。
– とりあえず下図みたいに書ける
– ここから、どう減らすのが最善かを考える
2016/3/20 12
１
２
３
４
５
６
７
１
２
３
１
２
３
４
５
６
１
２
３
４
５
１
２
３
１
２
３
４
１

• まず、赤く塗った部分は、前から繋がる部分が存在
しないので、絶対に塗らないといけない
• ここから右下に伸ばすと、全てを埋め尽くせる
– つまり、赤い部分を数えるだけで、手数が解る！
2016/3/20 13
１
２
３
４
５
６
７
１
２
３
１
２
３
４
５
６
１
２
３
４
５
１
２
３
１
２
３
４
１

パスに対する手数の求め方
• 赤い部分の数え方は非常に簡単
– 各マスについて、max(0, 1つ前のマスとの差+1)が、赤い
部分の個数になる。
• 前のマスより1つ下がったところが最高到達点となるため。
– これを利用すると、マスの順序をパスと呼び、その個数を
Lとすると、
• ライン全体の手数を求めるのは、ラインに含まれるすべてのマス
の赤い部分を調べれば良いので、O(L)
• ラインに1つマスを追加するのは、新規追加マスの赤い部分を調
べれば良いので、O(1)
• ライン2つの結合も、結合部分だけ調べれば良いのでO(1)
– 非常に早く計算出来る！
2016/3/20 14

貪欲法との違い
• 例えば、{8,7,6,5,4,4,3,2,1}みたいなのがあるとする
– 貪欲法だと、大体こんな感じになる
• 8,7,6,5,4を減らす
• 7,6,5,4,3を減らす
• 6,5,4,3,2を減らす
• ・・・・
• {4,3,2,1,0,4,3,2,1}になり、ここから、2つの4,3,2,1を減らす
– 12手？
– 今回の方法だと、もっと賢くなる
• 4,3,2,1を減らす
• {8,7,6,5,4,3,2,1, 0}になり、これを減らす
– 9手？
– 貪欲法で生じていた無駄が、パスを決めることでなくなった！
2016/3/20 15

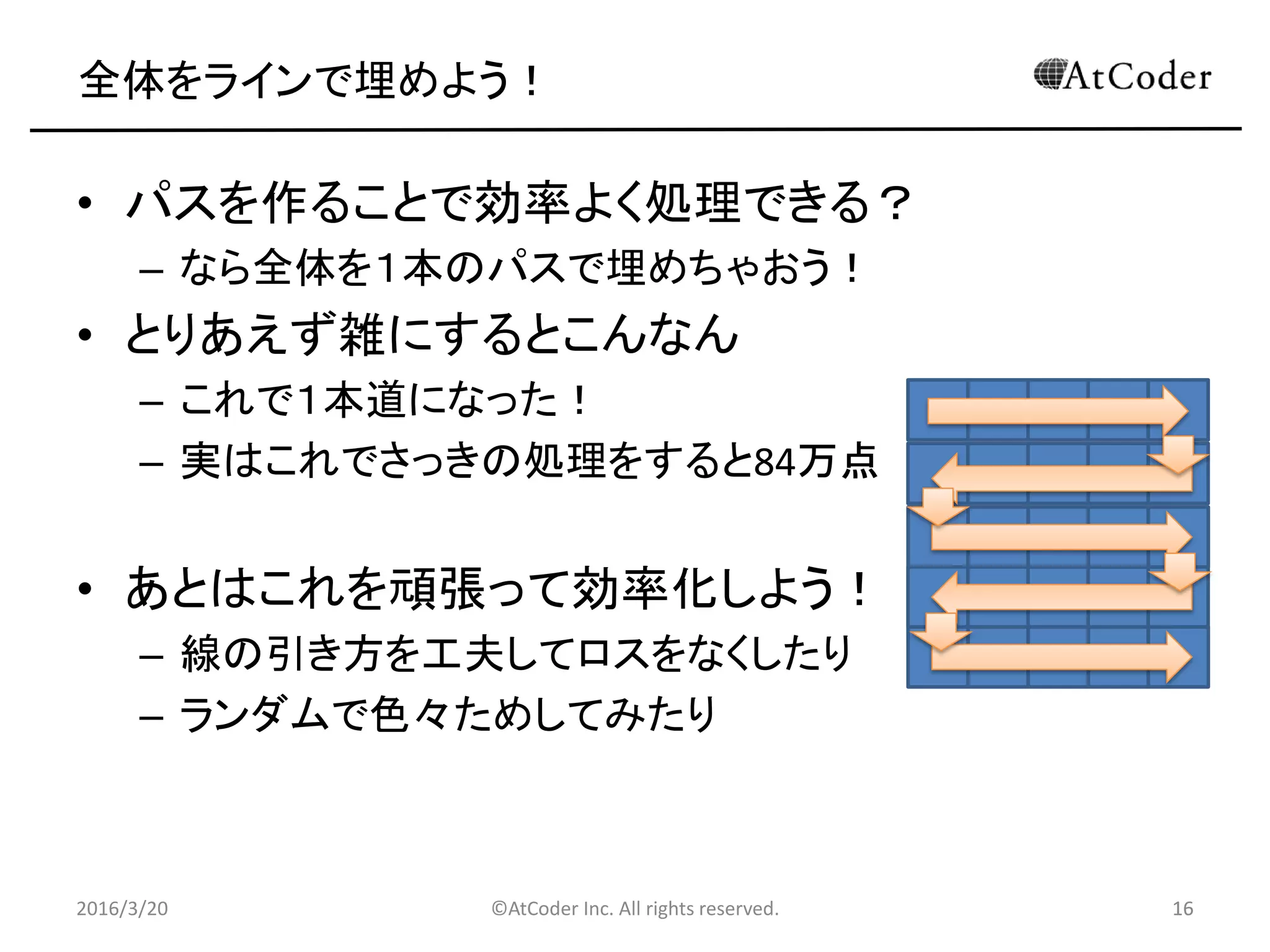
全体をラインで埋めよう！
• パスを作ることで効率よく処理できる？
– なら全体を１本のパスで埋めちゃおう！
• とりあえず雑にするとこんなん
– これで１本道になった！
– 実はこれでさっきの処理をすると84万点
• あとはこれを頑張って効率化しよう！
– 線の引き方を工夫してロスをなくしたり
– ランダムで色々ためしてみたり
2016/3/20 16

全体をパスで埋めないとだめ？
• さっきの例では全ての線を埋めたが、別に複数のパ
スがあっても問題ない
– 繋がっていない分ロスは生まれやすいが
• よって、実装が大変だったらこれでも良い
– これでも84万点近くに行きます。
2016/3/20 17

パスの作り方
• 隣り合う数の差が小さくなるようにパスを作ることで、
手数を減らすことが出来る
– つまり、パスの作り方で貪欲法を使う？
• これをすると、無駄な隙間が出来てしまい、あまり良
いスコアにならない
– 隙間が出来ないようにパスを作ろう
2016/3/20 18

パスの作り方探索編
• 例えばこの状態の時、
– たくさん埋まっているマスの評価を上げる
• ３方向から埋められているマスは超評価を上げる（赤）
• ２方向から埋められているマスは評価を上げる（緑）
• １方向から埋められているマスは普通の評価（青）
– 行き止まりに気を付ければ、良いパスが作りやすい！
• もうちょっと細かいところを気にした方がもちろん良い
– これを評価に加えて探索する
– 普通にやったら82万点くらい？
• まともなパスにするのはだいぶ難しい
– 凄く頑張ると88万点台？
• ビームサーチとかが使えます。
2016/3/20 19

パスの作り方 DP
• 探索は難しい！DPにしよう！
– dp[L][R][U][D][A][B]を使って状態を更新する
• 長方形(L, U)-(R, D)の区間が最大で、四隅に0,1,2,3と番号をつけ
た時に、パスの始点がA、終点がBな時の、最短手数を入れる
» 最短と言っても、あくまで「見つけた中での最短」
– 横に分割する時は、dp[L][X][U][D][A][i]と、
dp[X][R][U][D][j][B]を使って更新する。縦もやる。
• イメージはこんな感じ。切るx座標Xや、接続点iが複数ある。
2016/3/20 20

• このDPも更新の仕方を複数作れる
– 例えばこんな感じの分け方をすると、パスが2つ出来るが、
パスの始点・終点は維持される。
• もう一方は無視をするような形になる。
– こういう工夫を頑張って色々すると89万点に乗ります。
2016/3/20 21

• このDPも更新の仕方を複数作れる
– 例えばこんな感じの分け方をすると、パスが2つ出来るが、
パスの始点・終点は維持される。
• もう一方は無視をするような形になる。
– こういう工夫を頑張って色々すると89万点に乗ります。
2016/3/20 22

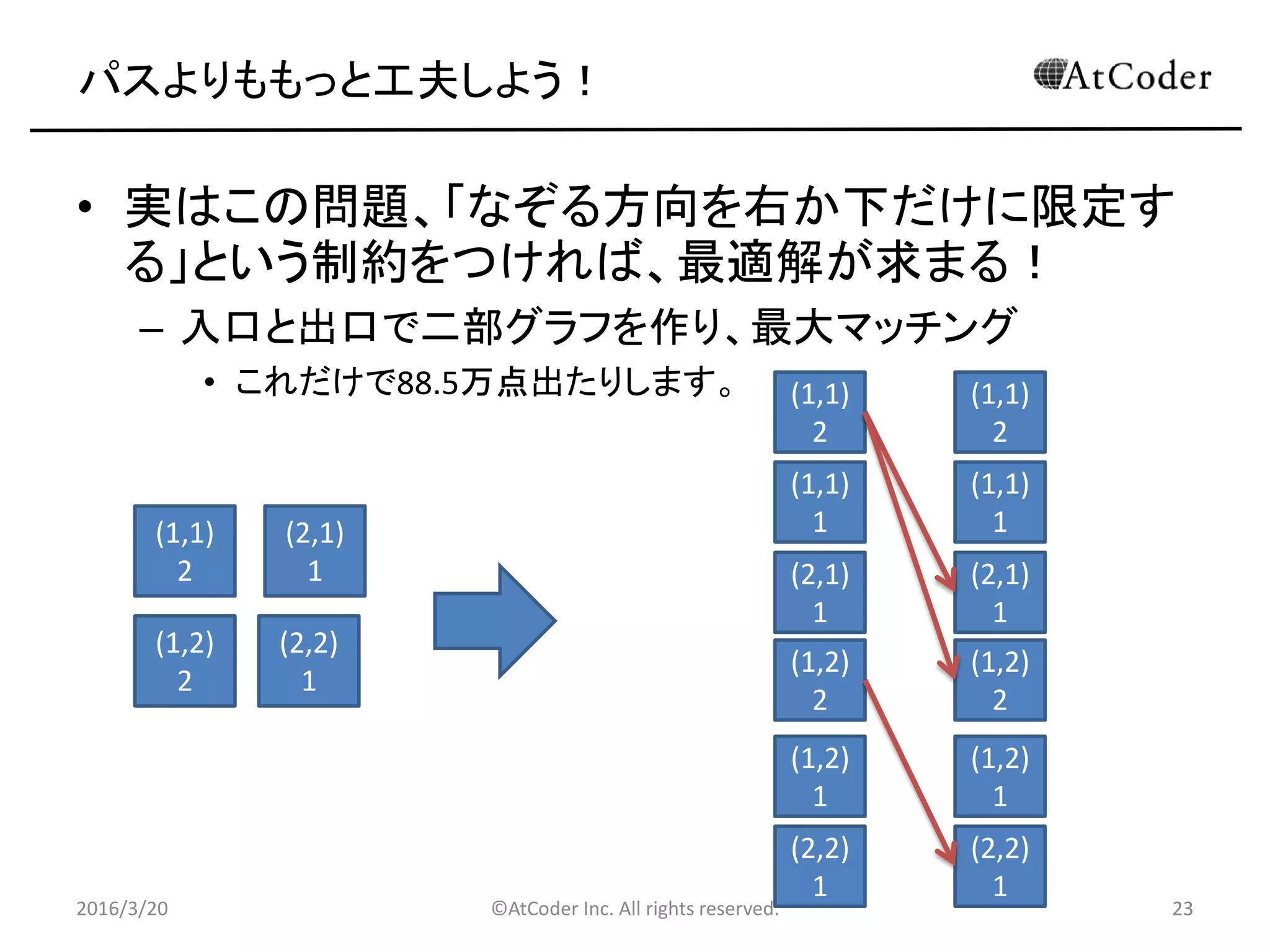
パスよりももっと工夫しよう！
• 実はこの問題、「なぞる方向を右か下だけに限定す
る」という制約をつければ、最適解が求まる！
– 入口と出口で二部グラフを作り、最大マッチング
• これだけで88.5万点出たりします。
2016/3/20 23
(1,1)
2
(2,1)
1
(1,2)
2
(2,2)
1
(1,1)
2
(1,1)
1
(2,1)
1
(1,2)
2
(1,2)
1
(2,2)
1
(1,1)
2
(1,1)
1
(2,1)
1
(1,2)
2
(1,2)
1
(2,2)
1

DAGの最適解が出ることを利用すると？
• なんでこれで解けるの？
– (1,1)の時点で10だったとして、(4,3)の時点では？
• 右に3回、下に2回移動しているので、絶対に5まで下がっている
• これは、移動方法に依存しない
– つまり、(A,B)時点でCの時、というパターンは、C-(A+B)が等しい
パターンしか通らない！
• 右下にしか行かない、という制約があるため
– よって、200枚程度のレイヤーに分かれた感じになるため、上レ
イヤーから順番に処理すれば、順番が前後するなどの事故が
起こらない。
• 中心位置を変えるなどをランダムで試したりすると89万
点弱まで出る！
– 今のところパス解法の方が強いですが、こっちも強くなるかも
2016/3/20 24

Chokudai Contest 001

More Related Content

What's hot

Viewers also liked

Similar to Chokudai Contest 001

More from AtCoder Inc.

Chokudai Contest 001