تتناول هذه الوثيقة تفاصيل معادلات التفاضلية العادية من الرتبة العليا، مع التركيز على معادلة كوشي-أويلر والطرق المستخدمة لحلها. يستعرض النص خصائص المعادلات المتجانسة وغير المتجانسة، ويقدم أمثلة توضيحية حول الحلول الأساسية. كما يتطرق إلى مفهوم الاستقلالية الخطية لمجموعة من الحلول المرتبطة بالمعادلات التفاضلية.

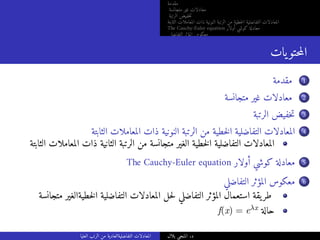
![مقدمة
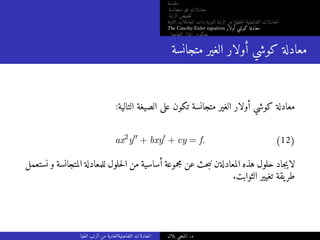
متجانسة غير معادلات
الرتبة خفيضت
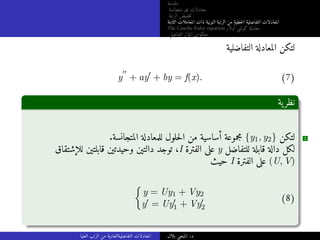
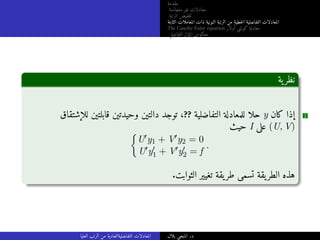
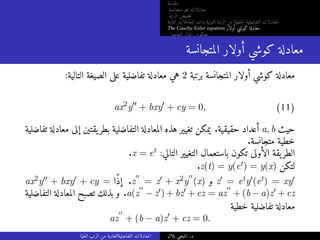
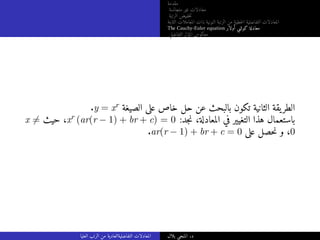
الثابتة المعاملات ذات النونية الرتبة من خطيةلا التفاضلية المعادلات
The Cauchy-Euler equation أولار كوشي معادلة
التفاضلي المؤثر معكوس
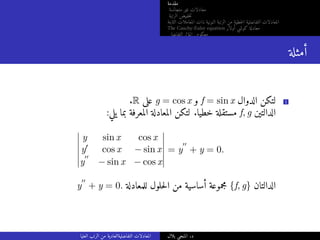
أمثلة
.[0,
π
2
] الفترة على خطيا مستقلة sin x, cos x الدوال 1
،x = 0 كان إذا فإنه ،x ∈ [0,
π
2
] لكل a sin x + b cos x = 0 كان إذا
.a = 0 فإن ،x =
π
2
كان إذا و b = 0
.مفتوحة فترة كل على خطيا مستقلة sin x, cos x أن نثبت أن يمكن
العليا الرتب من التفاضليةالعادية المعادلات بلال المنجي .د](https://image.slidesharecdn.com/chapter2-de-slides-220930185706-4f0b2c6c/85/chapter2-de-slides-pdf-7-320.jpg)
![مقدمة
متجانسة غير معادلات
الرتبة خفيضت
الثابتة المعاملات ذات النونية الرتبة من خطيةلا التفاضلية المعادلات
The Cauchy-Euler equation أولار كوشي معادلة
التفاضلي المؤثر معكوس
.[0,
π
2
] الفترة على خطيا مستقلة ex, sin x, cos(2x) الدوال 2
كان إذا فإنه ،x ∈ [0,
π
2
] لكل aex + b sin x + c cos(2x) = 0 كان إذا
.ae
π
2 + b = 0 ،x =
π
2
كان إذا و a + c = 0 ،x = 0
:على حصلن و بالإشتقاق نقوم أن كذلك يمكن
.x ∈ [0,
π
2
] لكل aex + b cos x − 2c sin(2x) = 0
بالتالي و .a = 0 و a + b = 0 على حصلن ،x =
π
2
و x = 0 كان إذا كذلك
.a = b = c = 0
.فترة كل على خطيا مستقلة ex, sin x, cos x أن نثبت أن يمكن
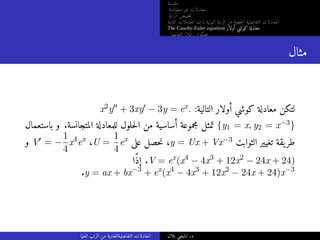
لأن فترة كل على خطيا مرتبطة sin x, cos x, sin(x + 1) الدوال 3
.sin(x + 1) = cos 1 sin x + sin 1 cos x
العليا الرتب من التفاضليةالعادية المعادلات بلال المنجي .د](https://image.slidesharecdn.com/chapter2-de-slides-220930185706-4f0b2c6c/85/chapter2-de-slides-pdf-8-320.jpg)


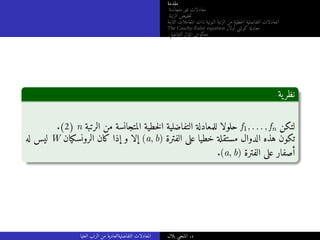
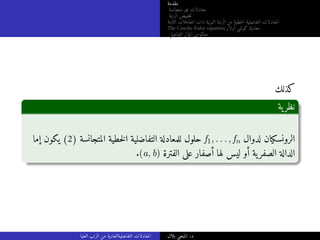
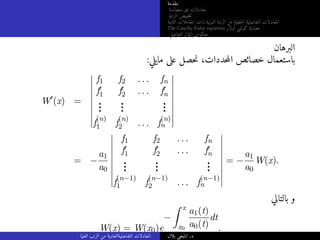


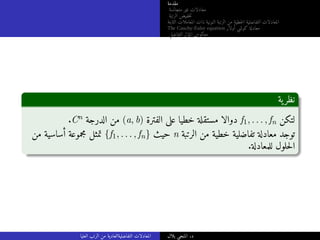


![مقدمة
متجانسة غير معادلات
الرتبة خفيضت
الثابتة المعاملات ذات النونية الرتبة من خطيةلا التفاضلية المعادلات
The Cauchy-Euler equation أولار كوشي معادلة
التفاضلي المؤثر معكوس
يةنظر
[ المتجانسة للمعادلة العام حللا ]
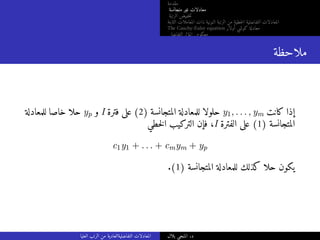
ليكن و ،I فترة على ((1) المتجانسة الغير التفاضلية للمعادلة حلا yp ليكن
فإن ،I على (2) المتجانسة التفاضلية للمعادلة حلوللا من أساسية مجموعة {y1, . . . , yn}
y = c1y1 + . . . + cnyn + yp
.c1, . . . , cn ∈ R حيث ،I الفترة على (1) للمعادلة حللا العام هو
العليا الرتب من التفاضليةالعادية المعادلات بلال المنجي .د](https://image.slidesharecdn.com/chapter2-de-slides-220930185706-4f0b2c6c/85/chapter2-de-slides-pdf-24-320.jpg)

![مقدمة
متجانسة غير معادلات
الرتبة خفيضت
الثابتة المعاملات ذات النونية الرتبة من خطيةلا التفاضلية المعادلات
The Cauchy-Euler equation أولار كوشي معادلة
التفاضلي المؤثر معكوس
يةنظر
[التراكب ]مبدأ
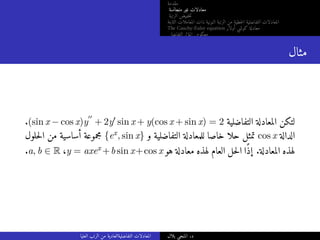
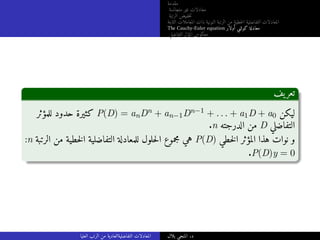
التفاضلية المعادلة لتكن
a0y(n)
+ a1y(n−1)
+ · · · + any = b1 + . . . + bm, (5)
.(a, b) فترة على متصلة دوال a0, . . . , an, b1, . . . , bm حيث
المتجانسة الغير التفاضلية للمعادلة خاصا حلا yk كان إذا
a0y(n)
+ a1y(n−1)
+ · · · + any = bk,
المتجانسة الغير التفاضلية للمعادلة خاص حل y1 + . . . + ym فإن ،1 ≤ k ≤ m لكل
.(5)
العليا الرتب من التفاضليةالعادية المعادلات بلال المنجي .د](https://image.slidesharecdn.com/chapter2-de-slides-220930185706-4f0b2c6c/85/chapter2-de-slides-pdf-27-320.jpg)




















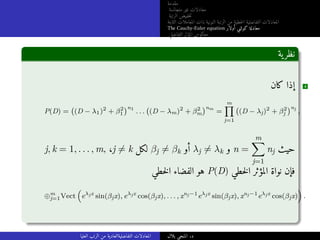
![مقدمة
متجانسة غير معادلات
الرتبة خفيضت
الثابتة المعاملات ذات النونية الرتبة من خطيةلا التفاضلية المعادلات
The Cauchy-Euler equation أولار كوشي معادلة
التفاضلي المؤثر معكوس
التفاضلي المؤثر معكوس
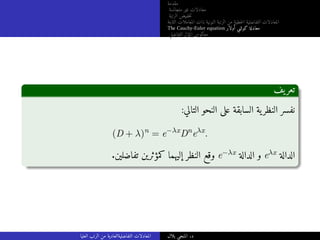
يفتعر
:على حصلن ،للتحليل الأساسية المبرهنة باستعمال .متصلة دالة f: [a, b] −→ R لتكن
d
dx
Z x
a
f(t)dt = D
Z x
a
f(t)dt = f(x).
::يلي ماك يفهتعر يمكن D التفاضلي للمؤثر D−1 التفاضلي المؤثر معكوس
D−1
f(x) =
Z x
a
f(t)dt.
،Dn التفاضلي المؤثر معكوس ياضيالر الإستقراء باستعمال نعرف كذلك
D−n
f(x) = D−n+1
(D−1
f(x)).
العليا الرتب من التفاضليةالعادية المعادلات بلال المنجي .د](https://image.slidesharecdn.com/chapter2-de-slides-220930185706-4f0b2c6c/85/chapter2-de-slides-pdf-61-320.jpg)