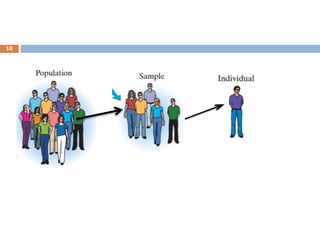
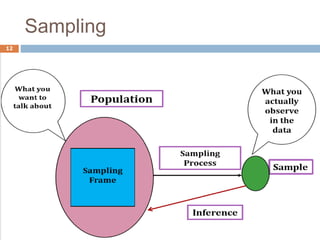
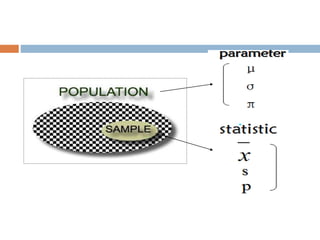
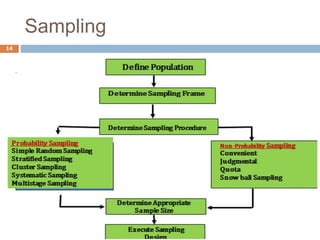
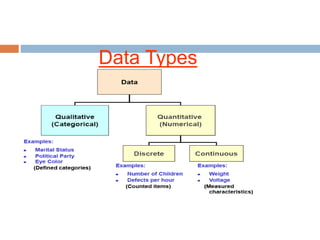
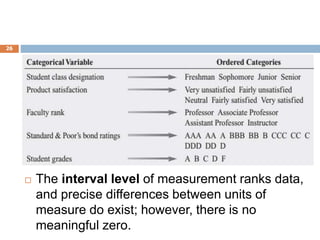
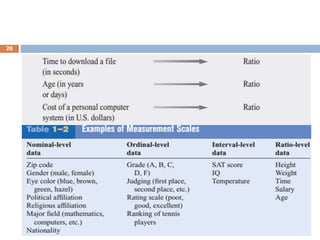
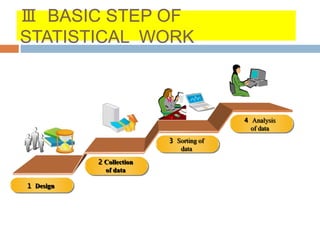
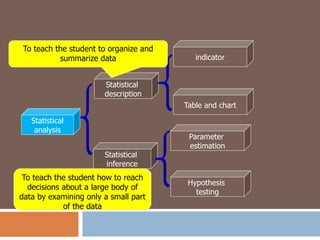
This document provides an introduction to biostatistics. It defines biostatistics as the application of statistical tools and concepts to data from biological sciences and medicine. The two main branches of statistics are described as descriptive statistics, which involves organizing and summarizing sample data, and inferential statistics, which involves generalizing from samples to populations. Several key statistical concepts are also defined, including populations, samples, variables, data types, levels of measurement, and common sampling methods. The objectives are to demonstrate knowledge of these fundamental statistical terms and concepts.

1. BIO STATISTICS

2. INTRODUCTION
CHAPTER ONE
2

3. Objectives of the chapter
 Demonstrate knowledge of statistical terms.
 Differentiate between the two branches of
statistics.
 Identify types of data.
 Identify the measurement level for each
variable.
 Identify the basic sampling techniques.
3

4. * Biostatistics:
4
 The tools of statistics are employed in many
fields:
business, education, psychology, agriculture,
economics, … etc.
 When the data analyzed are derived from the
biological science and medicine,
 we use the term biostatistics to distinguish this
particular application of statistical tools and
concepts.

5. Definition of Statistics?
 Statistics is the science of conducting studies
to collect, organize, summarize, analyze, and
draw conclusions from data.
 Statistics The science of collecting, describing,
and interpreting data.
 Statistics is the study of how to collect,
organize, analyze, and interpret numerical
information from data.
 Bio-statistics is the branch of applied statistics
that applies statistical methods to biological
science and medicine.
5

6. Types of Statistics
The two areas of Statistics are: Descriptive
statistics and Inferential statistic.
 Descriptive statistics involves methods of
collection, organizing, picturing, and
summarizing information from samples or
populations.
 Inferential statistics consists of generalizing
from samples to populations, performing
estimations and hypothesis tests, determining
relationships among variables, and making
predictions.
6

7.  In descriptive statistics the statistician tries to
describe a situation. Consider the national
census conducted by the Somaliland
government every 10 years. Results of this
census give you the average age, income, and
other characteristics of the Somaliland
population.
 The area of inferential statistics called
hypothesis testing is a decision-making
process for evaluating claims about a
population, based on information obtained
7

8. Reasons to study Statistics
 Statistics is an important tool for Planning, research, decision
making and problem solving.
 In diverse areas such as business, financial management, education
policy, we use statistical analysis to make decisions.
 It is a tool for scientific description and inference.
 It helps to know how to properly present information.
 It helps to recognize problems with published information.
 It helps to know how to draw appropriate conclusions from data.
 It helps to improve processes.
 To obtain reliable forecasts.
8

9.  A population consists of all subjects (human
or otherwise) that are being studied.
 Most of the time, due to the expense, time,
size of population, etc. it is not possible to use
the entire population for a statistical study;
therefore, researchers use samples.
 A sample is a group of subjects selected from
a population.
 An individual is a person or object that is a
member of the population being studied.
9

10. 10

11. Sampling
 Sampling is the process of selecting
observations (a sample) to provide an
adequate description and inferences of the
population.
 Sample
 It is a unit that is selected from population
 Represents the whole population
 Purpose to draw the inference
 Why Sample?
Sampling Frame Listing of population from
which a sample is chosen
11

12. Sampling
12

14. Sampling
14

15. Statistical Sampling: Items of the sample are chosen based on
known or calculable probabilities.
Simple Random Sampling : Every possible sample of a given
size has an equal chance of being selected. Selection may be
with replacement or without replacement.
Stratified Random Sampling : Divide population into
subgroups called strata according to some common
characteristic and select a simple random sample from each
subgroup and then combine samples from subgroups into
one.
Systematic Random Sampling : Decide on sample size :n.
Divide frame of N individuals into groups of k individuals
k=N/n. Randomly select one individual from the 1st group.
Select every kth individual thereafter.
Cluster Sampling : Divide populations into several “clusters”

16. Non Probability sampling
 Convenience Sampling
 Quota Sampling
 Judgmental Sampling (Purposive
Sampling)
 Snowball sampling
16

17. Non Probability sampling
 Convenience Sampling
 Convenience sampling involves choosing
respondents at the convenience of the
researcher
 Judgmental Sampling (Purposive Sampling
 Researcher employs his or her own "expert”
judgment about.
 Quota Sampling
 The population is first segmented into mutually
exclusive sub-groups, just as in stratified
17

18. Non Probability sampling
 Snowball sampling
 The research starts with a key person and
introduce the next one to become a chain
18

19. Variables and Types of Data
 To gain knowledge about seemingly
haphazard situations, statisticians collect
information for variables, which describe the
situation.
 A variable In statistics, variables are
measurable characteristics of things (persons,
objects, places, etc) that vary within a group of
such things
 Data is a collection of facts or measurements
attributed to an entity.
 Examples are a list of percentage scores of
19

20. Data Types

21. 21
Quantitative Variables
Definition
A variable that can be measured numerically is called a
quantitative variable. The data collected on a
quantitative variable are called quantitative data.
Qualitative or Categorical Variables
Definition
A variable that cannot assume a numerical value but
can be classified into two or more nonnumeric
categories is called a qualitative or categorical
variable. The data collected on such a variable are
called qualitative data.

22. 22
Quantitative Variables cont.
Definition
A variable whose values are countable is called a
discrete variable. In other words, a discrete
variable can assume only certain values with no
intermediate values.
Definition
A variable that can assume any numerical
value over a certain interval or intervals is
called a continuous variable.

23. Source of Data
JWP 2007 23
Routinely Kept Records: Day to day records or data kept by
institutions
Census: A count or measure of the entire population
Survey: A count or measure of part of the population.
Experiment: Apply treatment to a part of the group
External Sources: Data Exist in form published Report

24. Level (Scale) of Measurement
 The appropriateness of the data analysis
depends on the level of measurement of the
data gathered. Four common levels of data
measurement follow.
1. Nominal
2. Ordinal
3. Interval
4. Ratio
 The nominal level of measurement classifies
data into mutually exclusive (non-overlapping)
categories in which no order or ranking can be
24

25.  The ordinal level of measurement classifies
data into categories that can be ranked;
however, precise differences between the
ranks do not exist.
25

26.  The interval level of measurement ranks data,
and precise differences between units of
measure do exist; however, there is no
meaningful zero.
26

27.  The ratio level of measurement possesses all
the characteristics of interval measurement,
and there exists a true zero. In addition, true
ratios exist when the same variable is
measured on two different members of the
population.
27

28. 28

29. 1 Design
2 Collection
of data
3 Sorting of
data
4 Analysis
of data
Ⅲ BASIC STEP OF
STATISTICAL WORK

30. Statistical
description
Statistical
inference
indicator
Table and chart
Parameter
estimation
Hypothesis
testing
Statistical
analysis
To teach the student to organize and
summarize data
To teach the student how to reach
decisions about a large body of
data by examining only a small part
of the data

31. ANY QUESTION?
THANK YOU
31