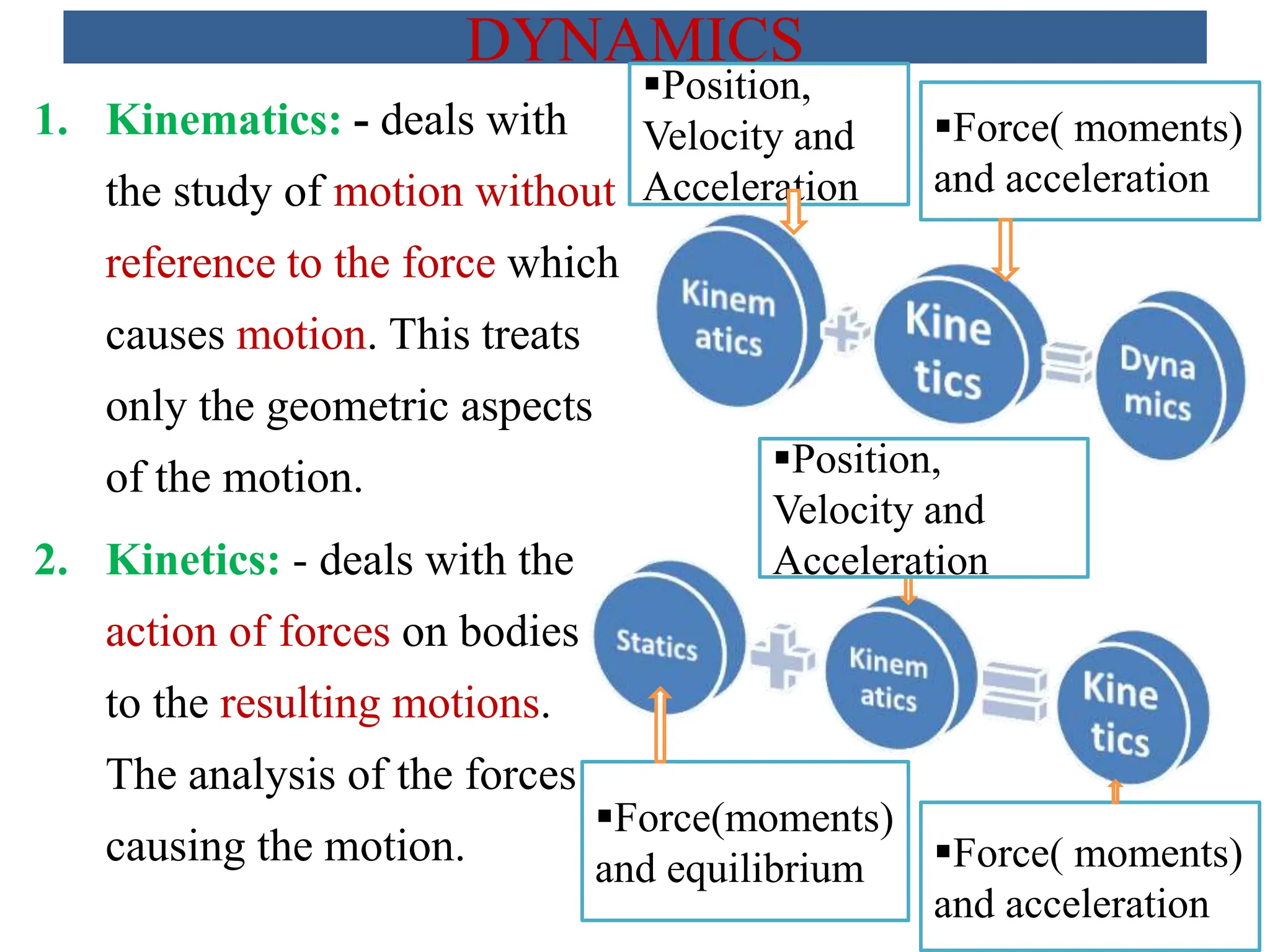
The document provides an overview of mechanics, specifically focusing on statics and dynamics within mechanical engineering. It outlines the concepts of motion, forces, kinematics, and kinetics, as well as Newton's laws of motion and gravitation. Additionally, it addresses the applications of dynamics in various fields such as robotics, transportation, and machinery.

1. Mechanical Engineering

2. DYNAMICS
Mechanics
• Mechanics is a branch of
the physical sciences
which is concerned with
the state of rest or motion
of bodies subjected to the
action of forces.
• Engineering mechanics is
divided into statics and
dynamics.
• Statics: - is concerned with the
equilibrium of body that either at
rest or moves with constant
velocity. It deals with the effect of
forces on a body at rest.
• Dynamics: - deals with the motion
of bodies under the action of
forces. It deals with the
accelerated motion body. It has
two distinct parts. kinematics and
kinetics.

3. DYNAMICS
1. Kinematics: - deals with
the study of motion without
reference to the force which
causes motion. This treats
only the geometric aspects
of the motion.
2. Kinetics: - deals with the
action of forces on bodies
to the resulting motions.
The analysis of the forces
causing the motion.
Position,
Velocity and
Acceleration
Force( moments)
and acceleration
Force(moments)
and equilibrium Force( moments)
and acceleration
Position,
Velocity and
Acceleration

4. DYNAMICS
Applications of dynamics
Used to analysis and design :
 moving structures and fixed
structures subjected to the shock
loads
 robotic devices, and automatic
control system
 rockets, missiles, and spacecraft,
 ground and air transportation
vehicles,
 electron ballistics of electrical
devices, and
 machinery of all types
Basic Concepts
 Time: measuring the succession
and the duration of events.
 Mass: a measure of the
translational inertia of the body,
which is its resistance to a
change in velocity
 Force: the action of one body
on another.
 Particle: is a body of negligible
dimensions.

5. DYNAMICS
 Rigid Body: is an idealized
body composed of a large
number of particles all of
which always remain at fixed
distances from each other. is
assumed to undergo no
deformation under the action of
applied forces.
 Point Force: is an idealized
force assumed to act at a point
on a body.
 Scalar: only magnitude is
associated. Examples of scalar
quantity are time, volume,
density, speed, energy, mass.
 Vector: possess direction as
well as magnitude. Examples of
vector quantity are
displacement, velocity,
acceleration, force, moment,
momentum.
Basic Concepts

6. DYNAMICS
1. Law I. A particle remains at
rest or continues to move with
uniform velocity (in straight
line with constant speed) if
there is no an unbalanced
force acting on it.
𝑭 = 0
2. Law II. The acceleration of a
particle is proportional to the
resultant force acting on it and is in
the direction of this force.
F = ma
Newton’s Laws

7. DYNAMICS
3. Law III. The forces of action
and reaction between interacting
bodies are equal in magnitude,
opposite in direction, and
collinear.
F = - F
Units
Four fundamental quantities of
mechanics. F =
𝑀𝐿
𝑇2
• F = ma → N = kg.m/s2
→ lb = slug.ft/ sec2
• W = mg → N = kg.m/s2
→ lb = slug.ft/ sec2
Newton’s Laws

8. DYNAMICS
• Every particle of matter in the
universe attracts every other
particle with a force that is
directly proportional to the
product of the masses of the
particles and inversely
proportional to the square of
the distance between them.
F = G
𝑚1𝑚2
𝑟2
Where F is the mutual force
attraction between the two
particles,
G = 6.67×10−11N⋅m2/kg2 is the
universal gravitational constant,
m1 and m2 are the masses of the
two particles, and
r is the distance between the
center of the two particles.
Gravitation

9. DYNAMICS
Weight of a body
If a particle is located at or near the
surface of the earth, the only
significant gravitational force is
that between the earth and the
particle.
Weight of a particle having mass
m1= m
Assuming earth to be a nonrotating
sphere of constant density and
having mass m2= Me
r = distance between the earth’s
center and the particle.
W = G
𝑚𝑚𝑒
𝑟2 , W = mg
mg = G
𝑚𝑚𝑒
𝑟2 , g = G
𝑚𝑒
𝑟2 = 9.81
m/s2 acceleration due to gravity.
If go represents the absolute
acceleration to gravity at sea level,
the absolute value at an altitude h
is R is the radius of the
Gravitation

10. If go represents the absolute acceleration to gravity at sea level, the
absolute value at an altitude h is
R is the radius of the earth.
Effect of a rotating earth
g = 9.80665(1+0.0052379sin 𝛾2) + 0.000023sin 𝛾4+……..), rotating
earth at sea level and at a latitude. 𝛾 is the latitude.
DYNAMICS

11. Questions
1. What is law of inertia?
2. What is gravitational force?
3. What is law of acceleration?
4. How does distance affect gravitational force?
5. What is the difference between mass and weight?
6. What is the relationship between force and
acceleration?
7. How is time measured in mechanics?
DYNAMICS

12. Questions
8. What is the equation to calculate gravitational
force between masses?
9. How does mass affect the acceleration of an
object?
DYNAMICS

13. Questions?
Comments?
Suggestions ?
DYNAMICS