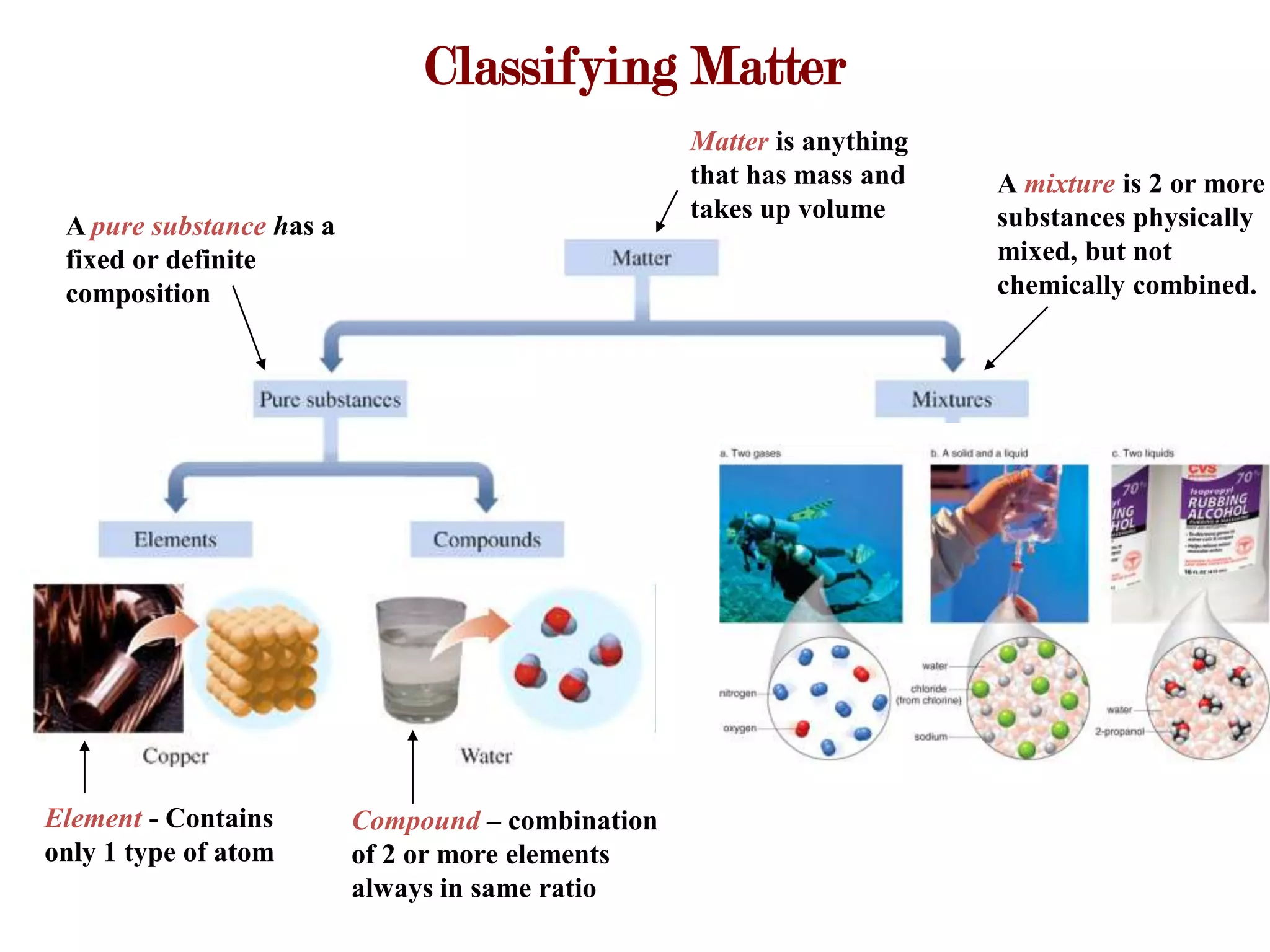
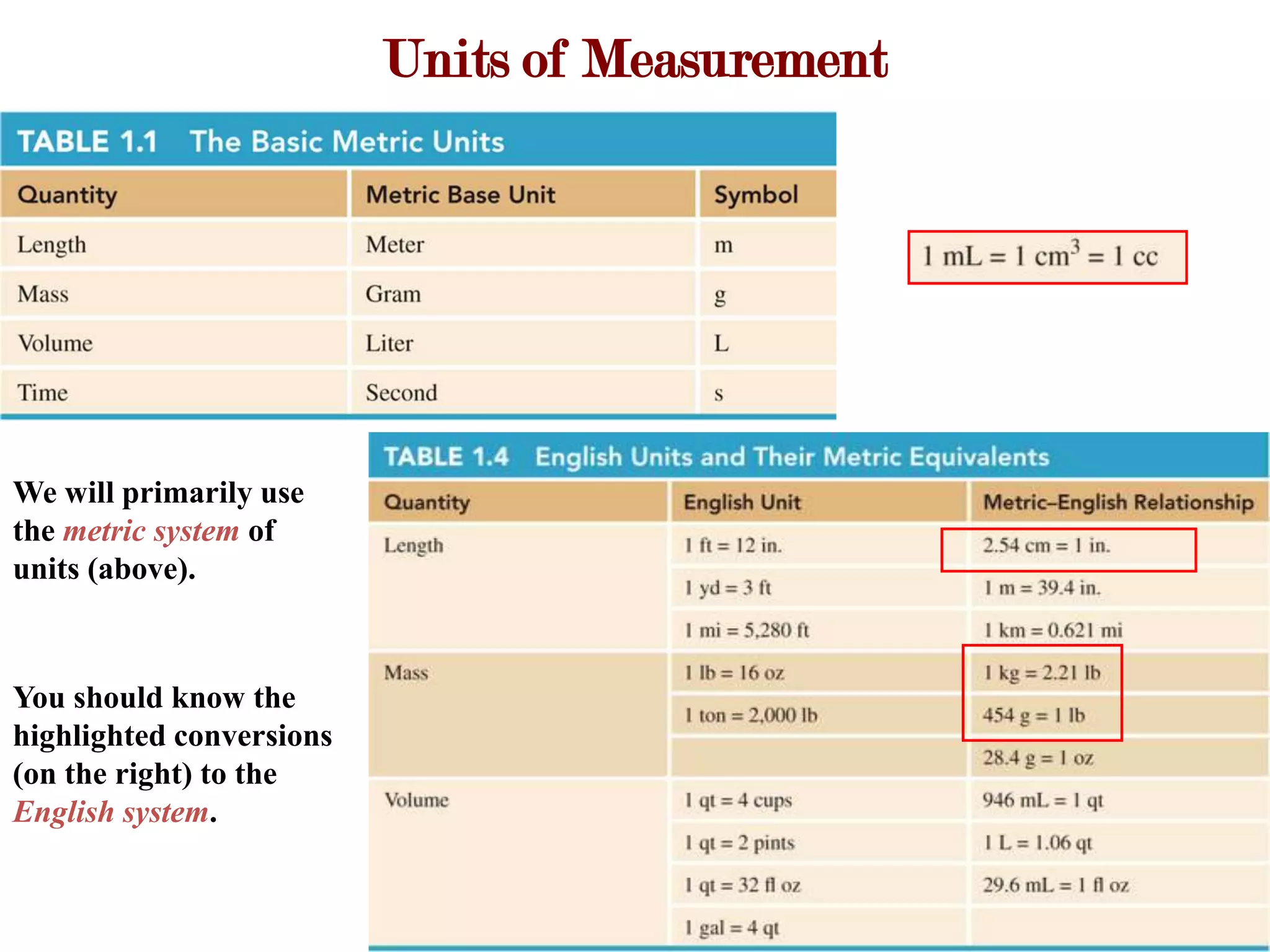
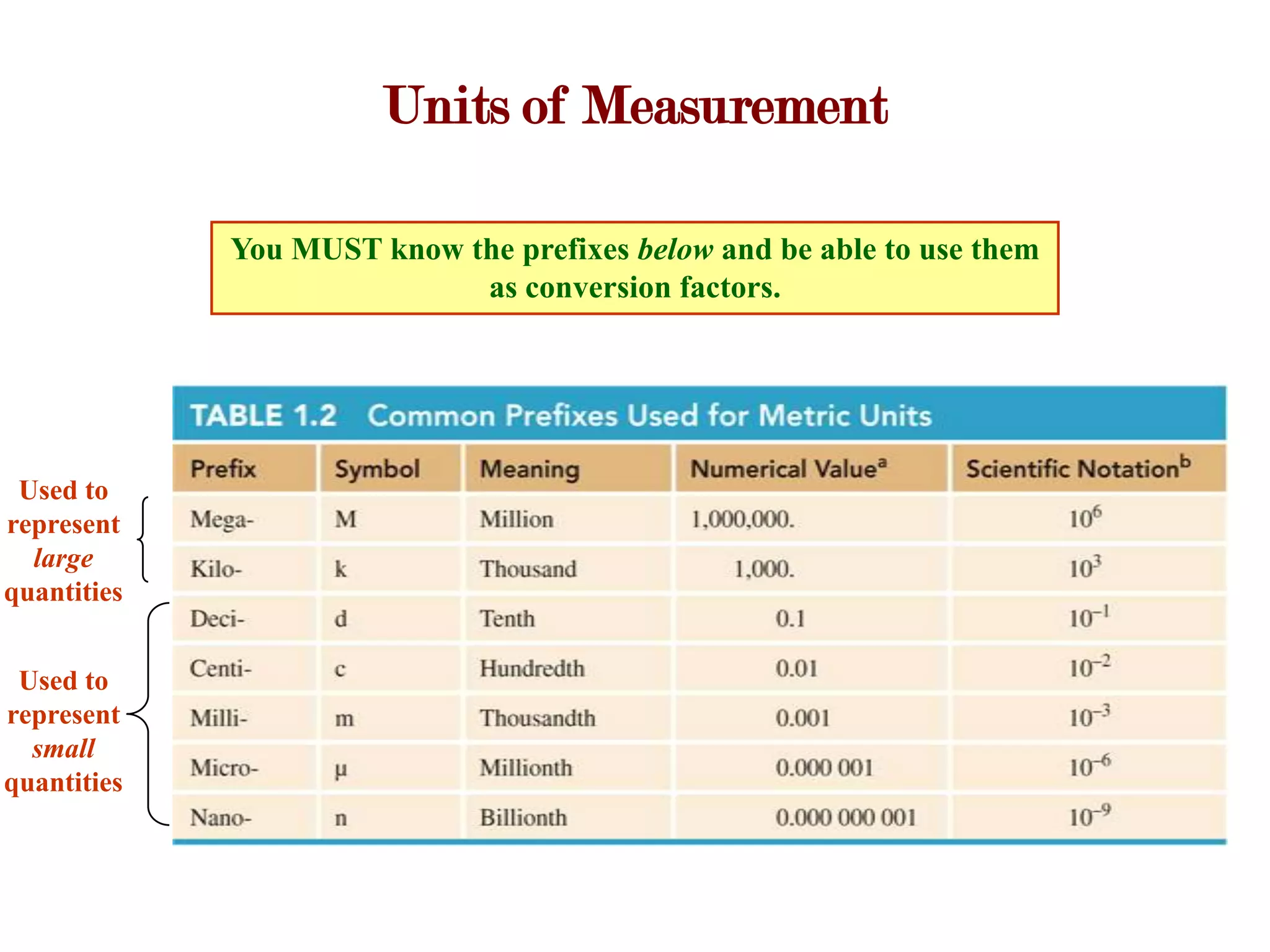
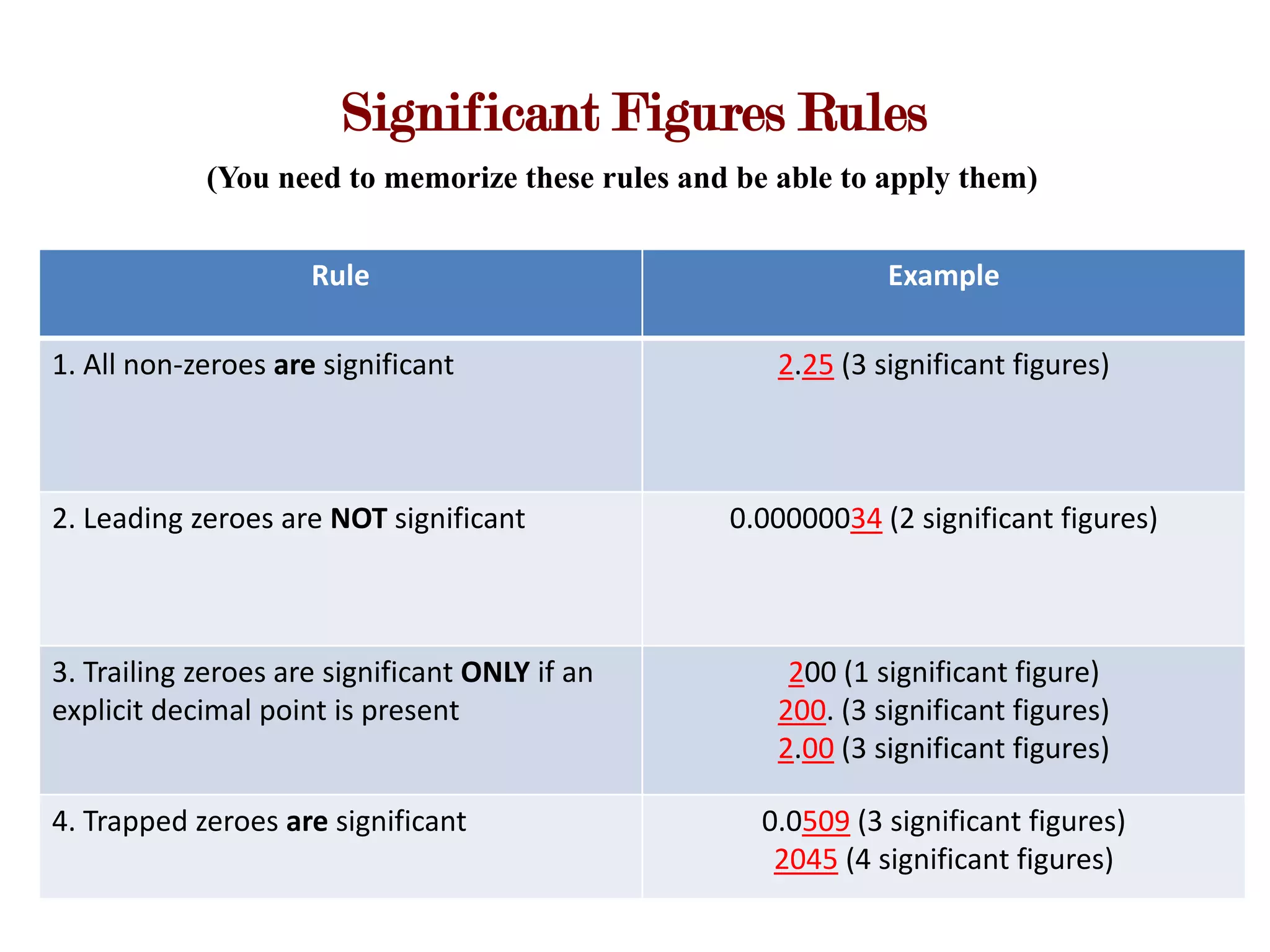
This document provides an overview of key concepts in classifying and measuring matter, including: - Pure substances can be elements or compounds, while mixtures contain two or more substances physically mixed. - The three common states of matter (solid, liquid, gas) have general characteristic properties. - Measurements involve a number and unit, and must be reported with the correct number of significant figures based on measurement precision. - Calculations with addition, subtraction, multiplication, and division require applying significant figure rules to determine the correct number of figures in the final answer.

1. 1/9/2013
CHM 101
Chapter 1: Matter & Measurement

2. Classifying Matter
Matter is anything
that has mass and A mixture is 2 or more
takes up volume substances physically
A pure substance has a
fixed or definite mixed, but not
composition chemically combined.
Element - Contains Compound – combination
only 1 type of atom of 2 or more elements
always in same ratio

3. Classifying Matter
Identify each of the following pure substances as examples of elements or compounds.

4. States of Matter
Identify general characteristics for each of the three states of matter below
(solid, liquid, gas).

5. Properties of Matter
Physical Changes
In the example below, water (H2O) is undergoing physical changes, from solid to
liquid to gas, but does not change its chemical identity.

6. Properties of Matter
Chemical properties identify a substance based on reactions with other substances.
Sodium (Na) (and other Group 1A Alkali metals) is known to react
violently with water (H2O).
2Na (s) + 2H2O (l)  2NaOH + H2 (g)
Chemical changes occur when one substance is converted into a different
substance, thus changing the chemical identity.
H2 (g) + O2 (g)  2H2O (g)

7. Chemical Change: Sodium in Water
2Na (s) + 2H2O (l)  2NaOH + H2 (g)

8. Measurements
Measurements always consist of a number and a unit.
The numbers in a measurement (measured numbers) should be carefully recorded
and reported.
From the example above, we know the length of the baby is 53.3 cm. We should use
all of the numbers given, but we can’t use any more.

9. Units of Measurement
We will primarily use
the metric system of
units (above).
You should know the
highlighted conversions
(on the right) to the
English system.

10. Units of Measurement
You MUST know the prefixes below and be able to use them
as conversion factors.
Used to
represent
large
quantities
Used to
represent
small
quantities

11. Precision in Measurements
• The tools that we use to measure matter can only be so precise
• For example, a ruler only has so many markings on it, which limits
one’s ability to determine a precise measurement between markings
• This brings us to a dreaded scientific concept: SIGNIFICANT
FIGURES!

12. Significant Figures
Exact (Defined) Values have an infinite number of SF’s.
12 eggs = 1 dozen
1 foot = 12 inches
Why are we concerned with SF’s?
If a reported result is based on several different measurements, the final result
can be no more precise than the least precise piece of information in the
calculation.
For example, if you take the mass of two items as 25.2 g and 1.34 g, how would
you report the total mass? 26.54 g or 26.5 g or 27 g????

13. Significant Figures Rules
(You need to memorize these rules and be able to apply them)
Rule Example
1. All non-zeroes are significant 2.25 (3 significant figures)
2. Leading zeroes are NOT significant 0.00000034 (2 significant figures)
3. Trailing zeroes are significant ONLY if an 200 (1 significant figure)
explicit decimal point is present 200. (3 significant figures)
2.00 (3 significant figures)
4. Trapped zeroes are significant 0.0509 (3 significant figures)
2045 (4 significant figures)

14. Significant Figures
Counting Significant Figures
Count all digits reading left to right, starting with the first non-zero digit.
How many significant figures are in the following measurements?
My answer Correct Answer
454 m
0.803 ft
0.0040 g
3000 lb
3000. lb
3.0 x 103 lb

15. Significant Figures in Calculations
Addition & Subtraction – the number of decimal places in the answer must equal the
# of decimal places in the value with the fewest decimal places.
Be careful! Your calculator doesn’t care about SF’s!!!
You have to decide how many digits to report.
25.2 one decimal place
+ 1.34 two decimal places
26.54 calculated answer
26.5 answer with one decimal place
*Report the sum with the correct number of SF’s: 3.008 g + 0.5 g = ?

16. Significant Figures in Calculations
Multiplication & Division – the number of SF’s in the answer must equal the number
of SF’s in the value with the fewest SF’s.
110.5 x 0.048 = 5.304 = 5.3 (rounded)
4 SF 2 SF calculator 2 SF
*Report the answer with the correct number of SF’s: 8.542 420 = ?
Throughout this course you will be expected to
report your answers with the correct number of
significant figures!!!

17. Rules for Rounding
 When the first digit dropped is less than 5 the retained numbers remain the same.
45.832 rounded to 3 significant figures drops the digits 32
= 45.8
 When the first digit dropped is greater than 5 the last retained digit is increased
by 1.
2.4884 rounded to 2 significant figures drops the digits 884
= 2.5

18. Rules for Rounding
 When the first digit dropped is exactly equal to 5, the last retained digit...
… stays the same if it is even.
1.45 rounded to 2 significant figures drops the digit 5
= 1.4
… increases by one if it is odd.
8.350 rounded to 2 sig figures drops the digits 50
= 8.4
*Round the following numbers to 4 significant figures:
45.385
27.2951
1.0025398
3.33359
When working a problem, do not round until all
calculations are complete. This will avoid introducing
round-off errors.