Recommended
DOCX
Дээд математик 3 MT103 бодлого
PDF
Exercícios de Trigonometria Resolvidos
PPT
PDF
1repaso ecuaciones 2º eso
PDF
Algebra cuaderno2eso ies bahia
PDF
DOCX
PDF
Chuyen de phuong trinh bac hai doi voi sin va cos
PPSX
PPS
PPT
PPT
Ideias da peça perfeita 2003
PPS
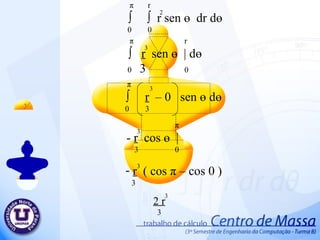
PPTX
PPT
PPSX
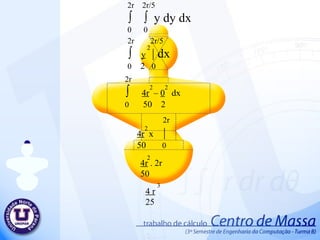
Geracao, Transmissao e Distribuicao de Energia Eletrica
PPT
PPSX
PPSX
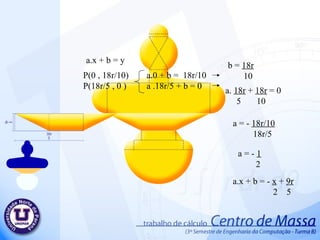
PPT
Trab calculo iii_pendulo3
PPS
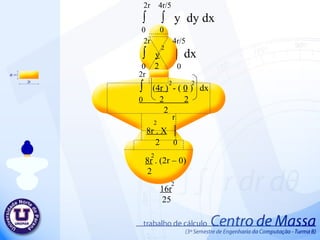
Cálculo rlc 97 definitivo
PPT
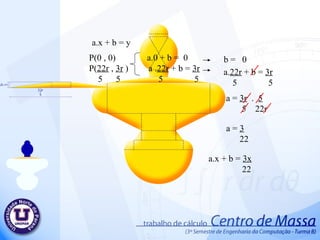
PPT
PPT
PPT
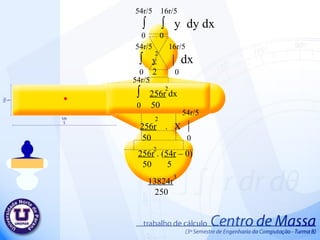
Apresentação circuito rc (atualizado)
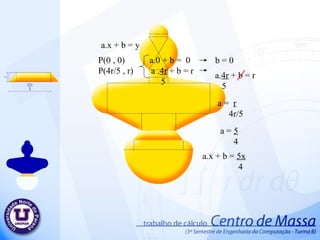
PPT
PPT
Trabalho de cálculo III cerveja
PPT
More Related Content
DOCX
Дээд математик 3 MT103 бодлого
PDF
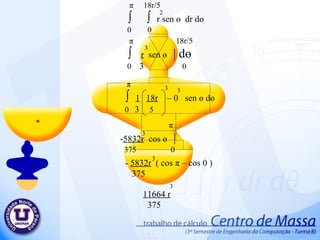
Exercícios de Trigonometria Resolvidos
PPT
PDF
1repaso ecuaciones 2º eso
PDF
Algebra cuaderno2eso ies bahia
PDF
DOCX
PDF
Chuyen de phuong trinh bac hai doi voi sin va cos
More from thiago oda
PPSX
PPS
PPT
PPT
Ideias da peça perfeita 2003
PPS
PPTX
PPT
PPSX
Geracao, Transmissao e Distribuicao de Energia Eletrica
PPT
PPSX
PPSX
PPT
Trab calculo iii_pendulo3
PPS
Cálculo rlc 97 definitivo
PPT
PPT
PPT
PPT
Apresentação circuito rc (atualizado)
PPT
PPT
Trabalho de cálculo III cerveja
PPT
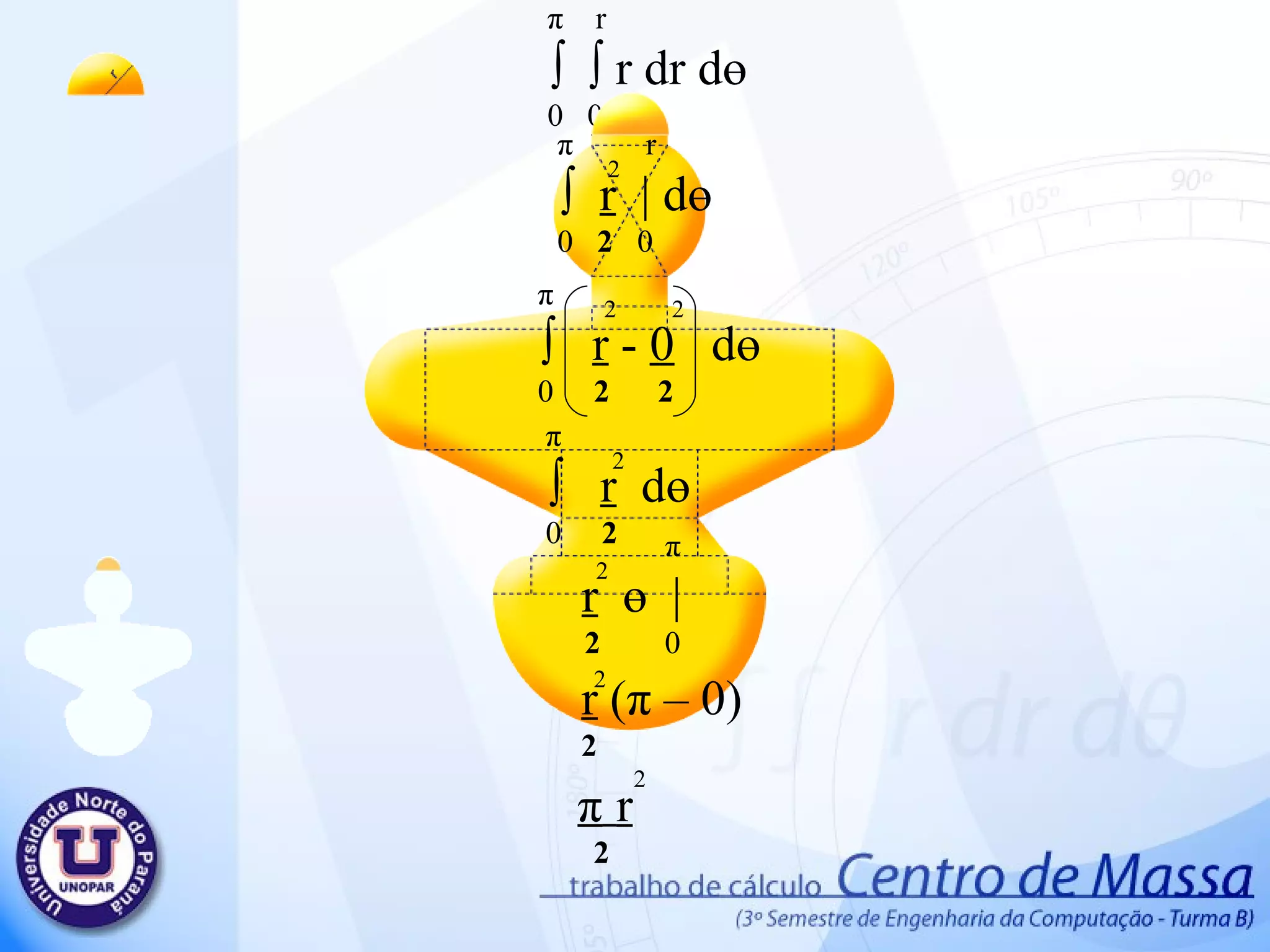
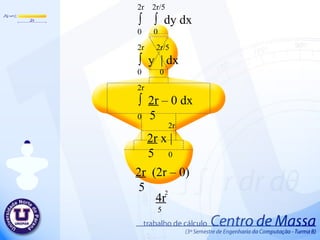
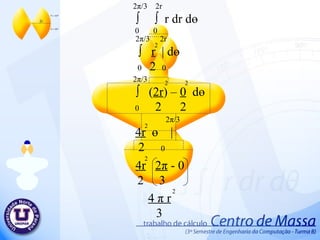
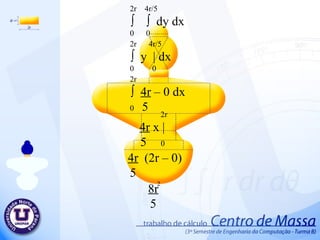
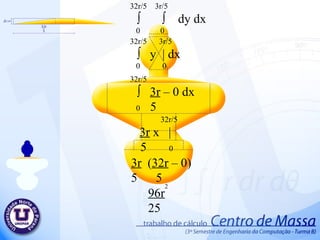
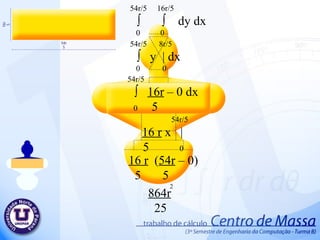
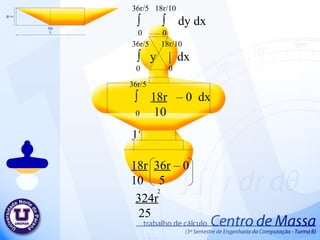
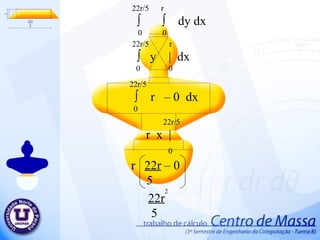
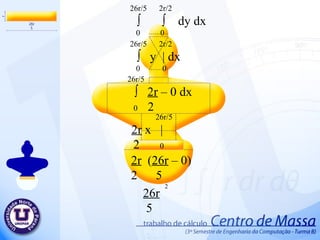
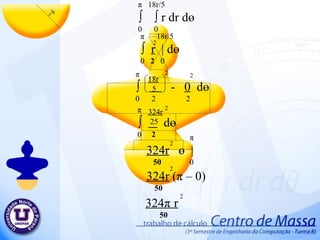
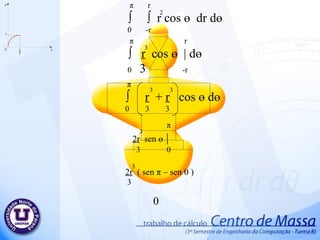
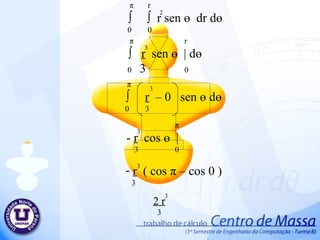
Centro de massa 1. π r ∫ ∫ r dr d ө 0 0 π r ∫ r | d ө 0 2 0 2 π ∫ r - 0 d ө 0 2 2 2 2 π ∫ r d ө 0 2 2 π r ө | 2 0 2 r ( π – 0) 2 π r 2 2 2 2. 2r 2r/5 ∫ ∫ dy d x 0 0 2r 2r/5 ∫ y | d x 0 0 2r ∫ 2r – 0 d x 0 5 2r 2r x | 5 0 2r (2r – 0) 5 4r 5 2 3. 2 π /3 ∫ ( 2r ) – 0 d ө 0 2 2 2 π /3 2r ∫ ∫ r dr d ө 0 0 2 π /3 2r ∫ r | d ө 0 2 0 2 2 2 2 π /3 4r ө | 2 0 2 4r 2 π - 0 2 3 2 4 π r 3 2 4. 5. r r √ 3 ∫ ∫ dy d x 0 0 r r √3 ∫ y | d x 0 0 r ∫ r √3 – 0 d x 0 r r √3 x | 0 r √3 (r – 0) r √3 2 r √3 2 6. 7. 2r 4r/5 ∫ ∫ dy d x 0 0 2r 4r/5 ∫ y | d x 0 0 2r ∫ 4r – 0 d x 0 5 2r 4r x | 5 0 4r (2r – 0) 5 8r 5 2 8. 32r/5 3r/5 ∫ ∫ dy d x 0 0 32r/5 3r/5 ∫ y | d x 0 0 32r/5 ∫ 3r – 0 d x 0 5 32r/5 3r x | 5 0 3r ( 32r – 0) 5 5 96r 25 2 9. 54r/5 16r/5 ∫ ∫ dy d x 0 0 54r/5 8r/5 ∫ y | d x 0 0 54r/5 ∫ 16r – 0 d x 0 5 54r/5 16 r x | 5 0 16 r ( 54r – 0) 5 5 864r 25 2 10. π 8r/5 ∫ ∫ r dr d ө 0 0 π 8r/5 ∫ r | d ө 0 2 0 π ∫ 8r – 0 d ө 0 5 π 64r ө | 25 0 64r ( π – 0) 25 64 π r 25 2 2 2 2 2 2 11. 12. 36r/5 18r x | 10 0 36r/5 18r/10 ∫ ∫ dy dx 0 0 36r/5 18r/10 ∫ y | d x 0 0 36r/5 ∫ 18r – 0 d x 0 10 18r 36r – 0 10 5 324r 25 2 13. 22r/5 r ∫ ∫ dy dx 0 0 22r/5 r ∫ y | d x 0 0 22r/5 ∫ r – 0 d x 0 22r/5 r x | 0 r 22r – 0 5 22r 5 2 14. 26r/5 2r/2 ∫ ∫ dy d x 0 0 26r/5 2r/2 ∫ y | d x 0 0 26r/5 ∫ 2r – 0 d x 0 2 26r/5 2r x | 2 0 2r ( 26r – 0) 2 5 26r 5 2 15. π ∫ r - 0 d ө 0 2 2 π r ∫ ∫ r dr d ө 0 0 π r ∫ r | d ө 0 2 0 2 2 2 π ∫ r d ө 0 2 2 π r ө | 2 0 2 r ( π – 0) 2 π r 2 2 2 16. π ∫ - 0 d ө 0 2 2 π 18r/5 ∫ ∫ r dr d ө 0 0 π 18r/5 ∫ r | d ө 0 2 0 2 π ∫ d ө 0 2 2 π 324r ө | 50 0 2 324r ( π – 0) 50 324 π r 50 2 2 18r 5 2 2 324r 25 17. π r 2 2 4r 5 2 8 π r 3 2 2 r √3 2 8r 5 2 96r 25 2 64 π r 25 2 324r 25 2 22r 5 2 26r 5 2 π r 2 2 324 π r 50 2 + + + + + + + + + + + = 75 π r +120r +400 π r +300r √3 +240r +576 r + 2592 r + 384 π r + 1944r + 660r + 780r+75 π r + 972 π r 150 2 2 2 2 2 2 2 ∑ A 2 2 2 2 2 = 1906 π r +300 r √3 +6912r 150 2 2 2 ∑ A = 864r 25 2 + 2 18. 19. π r ∫ ∫ r cos ө dr d ө 0 -r π r ∫ r cos ө | d ө 0 3 -r π ∫ r + r cos ө d ө 0 3 3 π 2r sen ө | 3 0 3 3 3 2 2r ( sen π – sen 0 ) 3 3 0 3 20. 21. π r ∫ ∫ r sen ө dr d ө 0 0 π r ∫ r sen ө | d ө 0 3 0 π ∫ r – 0 sen ө d ө 0 3 π - r cos ө | 3 0 3 3 3 2 r ( cos π – cos 0 ) 3 3 2 r 3 3 22. 2 r 3 3 π r 2 2 Área . 2 π r 2 2r 3 π 23. 2r 2r/5 ∫ ∫ y dy d x 0 0 2r 2r/5 ∫ y | dx 0 2 0 2r ∫ 4r – 0 dx 0 50 2 2r 4r x | 50 0 2 2 2 4r . 2r 50 4 r 25 3 2 2 24. 4 r 25 3 Área 4r 5 2 . 5 4r 2 r 5 25. 2 π /3 2r ∫ ∫ r sen ө dr d ө 0 0 2 π /3 2r ∫ r sen ө | d ө 0 3 0 2 π /3 ∫ 2r – 0 sen ө d ө 0 3 2 π /3 - 8 r cos ө | 3 0 3 3 3 2 r ( cos 2 π – cos 0 ) 3 3 3 21 r 3 3 4 r 3 26. 4 r 3 Área 4 π r 3 2 . 3 4 π r 3r π 2 27. P(0 , r √3 ) a.0 + b = r √3 P(r , 0) a .r + b = 0 a.r + r √3 = 0 a = - r√3 r a = -√3 a.x + b = -√3x + r√3 b = r√3 a.x + b = y a.r + b = 0 28. r -x√3 + r √3 ∫ ∫ y dy d x 0 0 r -x√3 + r √3 ∫ y | dx 0 2 0 r ∫ (-x√3 + r√3 ) - ( 0 ) dx 0 2 2 r ∫ 3x + 2( -x √3 )( r √3 ) +3r dx 0 2 2 2 2 2 2 r ∫ 3x – 6xr + 3r dx 0 2 2 2 2 r 3x – 6xr + 3r x dx | 3 2 0 2 3 2 2 = r – 3r + 3r 2 3 3 3 r 2 3 = 29. 30. 2r 4r/5 ∫ ∫ y dy d x 0 0 2r 4r/5 ∫ y | dx 0 2 0 2r ∫ ( 4r ) - ( 0 ) dx 0 2 2 2 r 8r . X | 2 0 2 2 2 8r . (2r – 0) 2 2 2 16r 25 2 31. 16r 25 2 Área 864r 25 2 . 25 864r 2 2r 5 32. P(0 , 0) a.0 + b = 0 P( 22r , 3r ) a . 22r + b = 3r 5 5 5 5 a = 3r . 5 5 22r a = 3 22 a.x + b = 3x 22 b = 0 a.x + b = y a. 22r + b = 3r 5 5 33. 22r/5 3x/22 ∫ ∫ y dy d x 0 0 22r/5 3x/22 ∫ y | dx 0 2 0 22r/5 ∫ 3x - 0 dx 0 22 22 2 22r/5 9 . X | 968 3 0 2 2 2 3 . ( 22r – 0) 5 . 968 3 3 3993r 15125 3 34. 3993r 15125 3 Área 33r 25 2 . 25 33r 2 1331r 6655 35. 54r/5 16r/5 ∫ ∫ y dy d x 0 0 54r/5 16r/5 ∫ y | dx 0 2 0 54r/5 ∫ 256r dx 0 50 54r/5 256r . X | 50 0 2 2 256r . ( 54r – 0) 50 5 2 2 13824r 250 3 36. P(0 , 18r/10) a.0 + b = 18r/10 P(18r/5 , 0 ) a .18r/5 + b = 0 a = - 18r/10 18r/5 a = - 1 2 a.x + b = - x + 9r 2 5 b = 18r 10 a.x + b = y a. 18r + 18r = 0 5 10 37. 18r/5 -x/2 + 9r/5 ∫ ∫ y dy d x 0 0 18r/5 -x/2 + 9r/5 ∫ y | dx 0 2 0 18r/5 ∫ 1 - x + 9r - 0 dx 0 2 2 5 2 2 18r/5 ∫ 1 x + 2 - x 9r + 81r dx 0 2 4 2 5 25 2 18r/5 ∫ x - 18rx + 81r dx 0 8 20 50 2 2 18r/5 1 . x - 9r . x + 81r . x | 8 3 10 2 50 0 2 3 2 972 r 500 3 = 38. 39. P(0 , 0) a.0 + b = 0 P(4r/5 , r) a . 4r + b = r 5 a = r 4r/5 a = 5 4 a.x + b = 5x 4 b = 0 a.x + b = y a. 4r + b = r 5 40. 4r/5 5x/4 ∫ ∫ y dy d x 0 0 4r/5 5x/4 ∫ y | dx 0 2 0 18r/5 ∫ 1 5x - 0 dx 0 2 4 2 2 18r/5 ∫ 1 25x dx 0 2 16 2 18r/5 25 x | 3 0 32 3 2 1458r 120 3 41. 1458r 120 3 Área 2r 5 2 . 5 2r 2 7290r 240 42. π r ∫ ∫ r sen ө dr d ө 0 0 π r ∫ r sen ө | d ө 0 3 0 π ∫ r – 0 sen ө d ө 0 3 π - r cos ө | 3 0 3 3 3 2 r ( cos π – cos 0 ) 3 3 2 r 3 3 43. 2 r 3 3 π r 2 2 Área . 2 π r 2 2r 3 π 44. π 18r/5 ∫ ∫ r sen ө dr d ө 0 0 π 18r/5 ∫ r sen ө | d ө 0 3 0 π ∫ 1 18r – 0 sen ө d ө 0 3 5 π - 5832r cos ө | 375 0 3 3 3 2 - 5832r ( cos π – cos 0 ) 375 3 11664 r 375 3 3 45. 46. 47. ∑ Yg = 7,2 . 245.437 + 15 . 125 + 39,15 . 1850,263 + 65,800 . 250 + 75,800 . 600 + 16.678,637 98,300 . 6656,637 + 125,800 . 2025 + 149,14 . 687,5 + 160,495 . 1057,937 = 16.678,637 ∑ yg = 114,526229587 48. Deficiência no corte do objeto. Dilatação do objeto. Medidas imprecisos. Irregularidade do material do objeto. Arredondamentos nos resultados Possíveis erros no Projeto Tentativa para minimizar os possíveis erros Substituir os valores só no final dos cálculos. Guardar o objeto em local seco, para evitar a dilatação do objeto. Elaborar projeto a partir de desenhos com medidas precisos. 49. Professor: Valdemir Antunes Alunos: Keny Shindi Shiraishi Rafael Milani de Abreu Wagner Fedrigo Camargo Yuri Silvestre Barbosa Centro de Massa UNOPAR Universidade Norte do Paraná Editor's Notes #2 Inserir animação da área 1 – Animação 4 é ref ao desenho pequeno #3 1- desenho pequeno 2-desenho grande (saída) #4 1 – desenho pequeno 2 – saída desenho principal #6 1 – desenho peq 2 – desenho princ (saída) #8 1 – desenho peq 2 – desenho princ (saída)