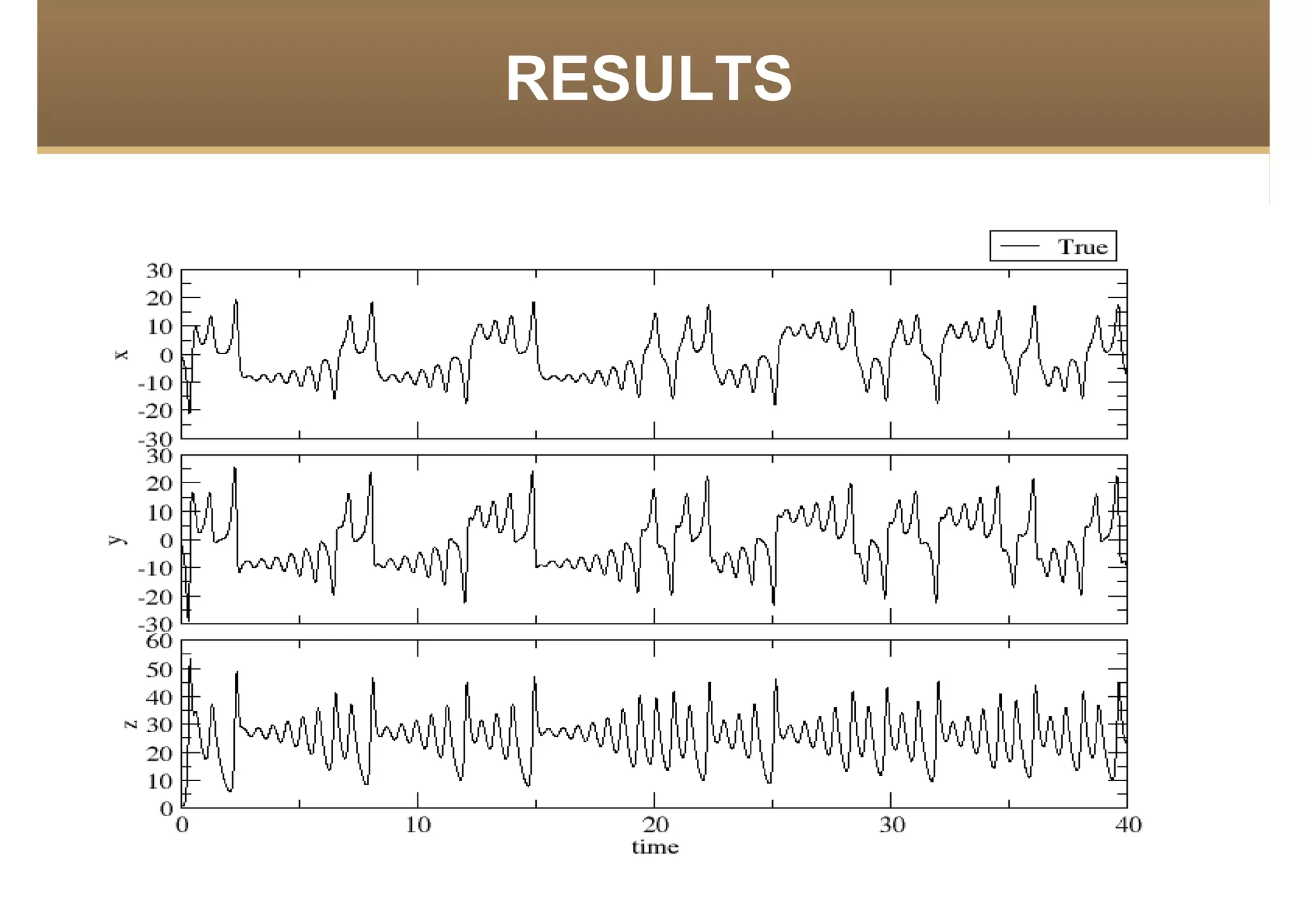
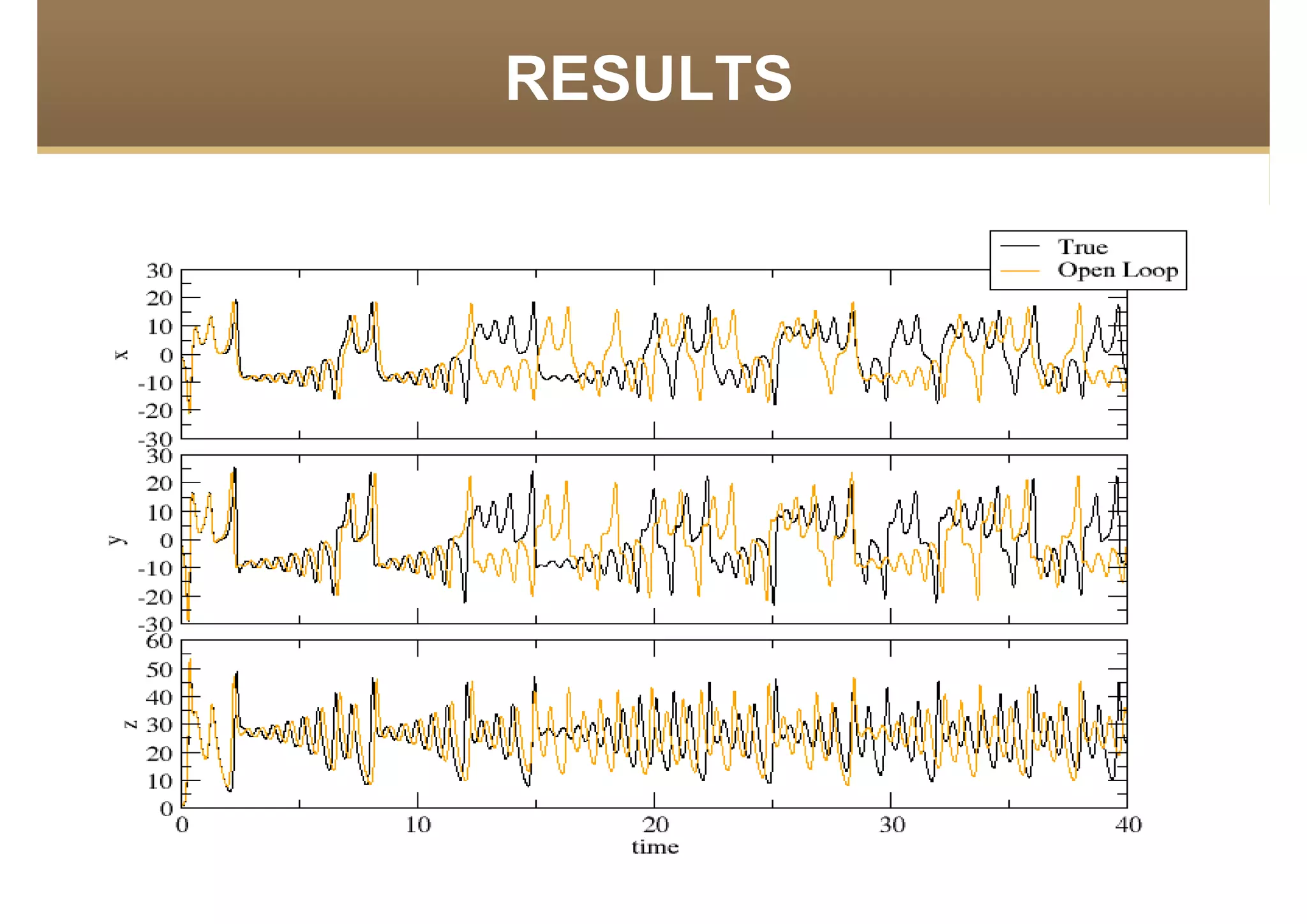
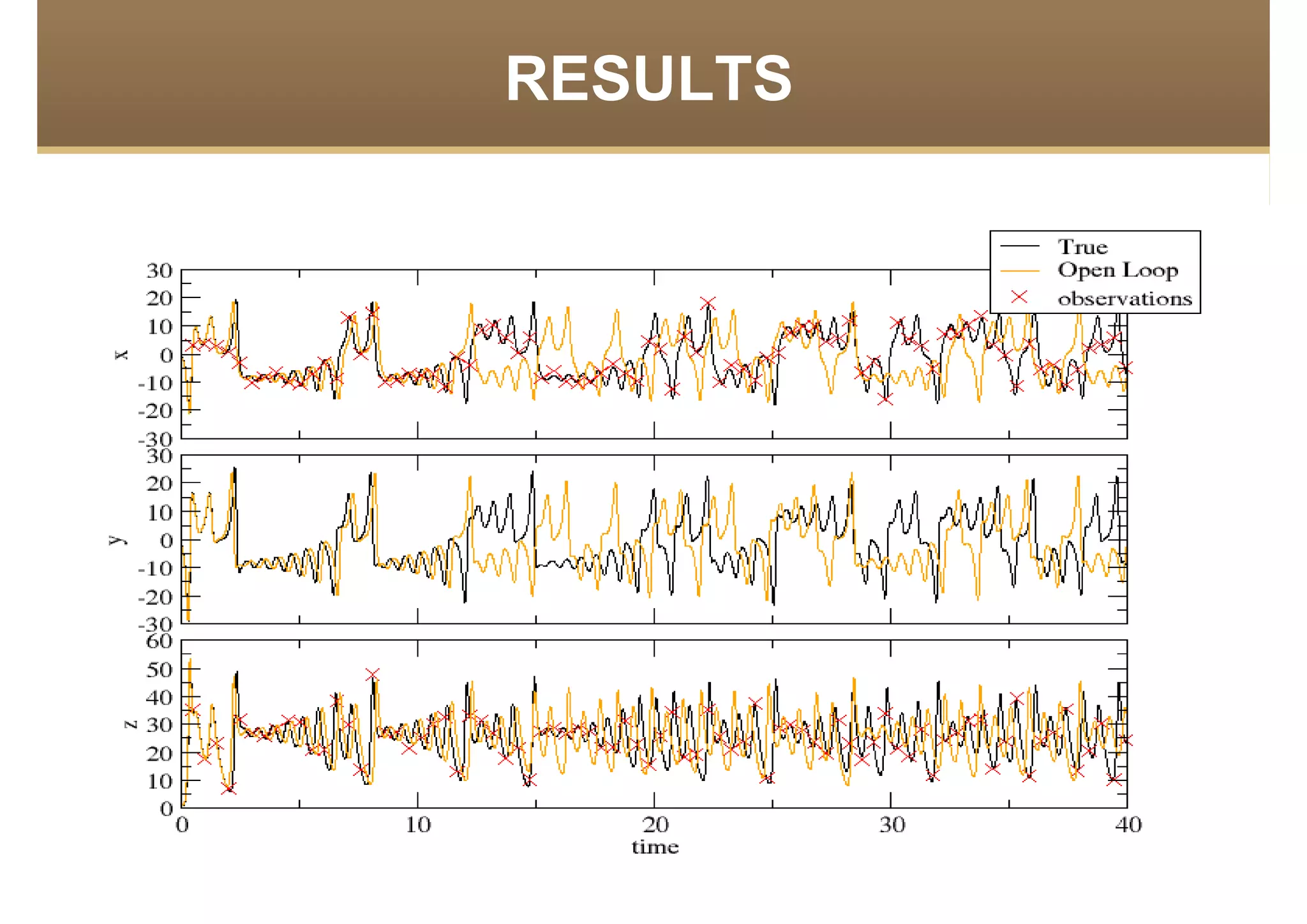
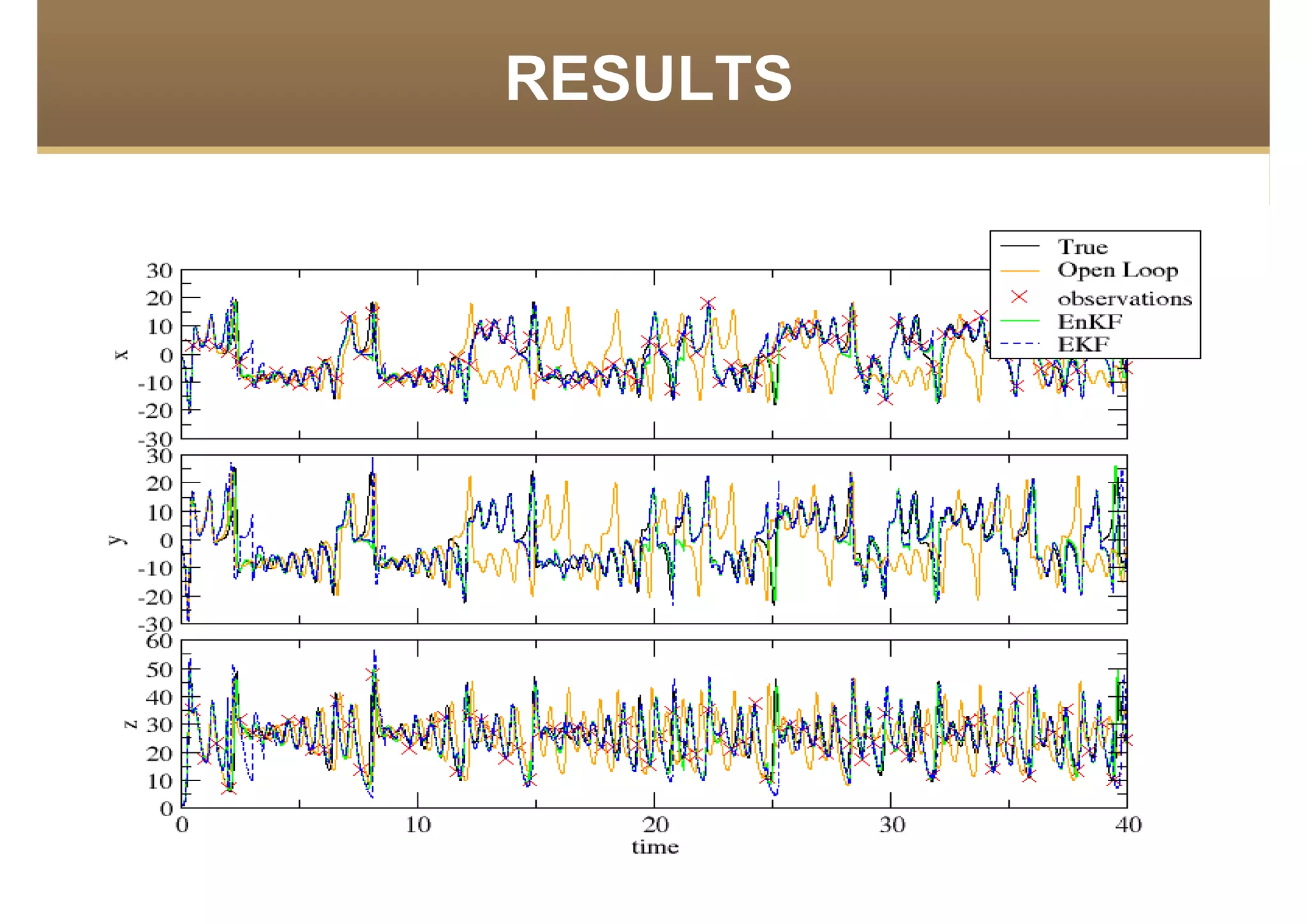
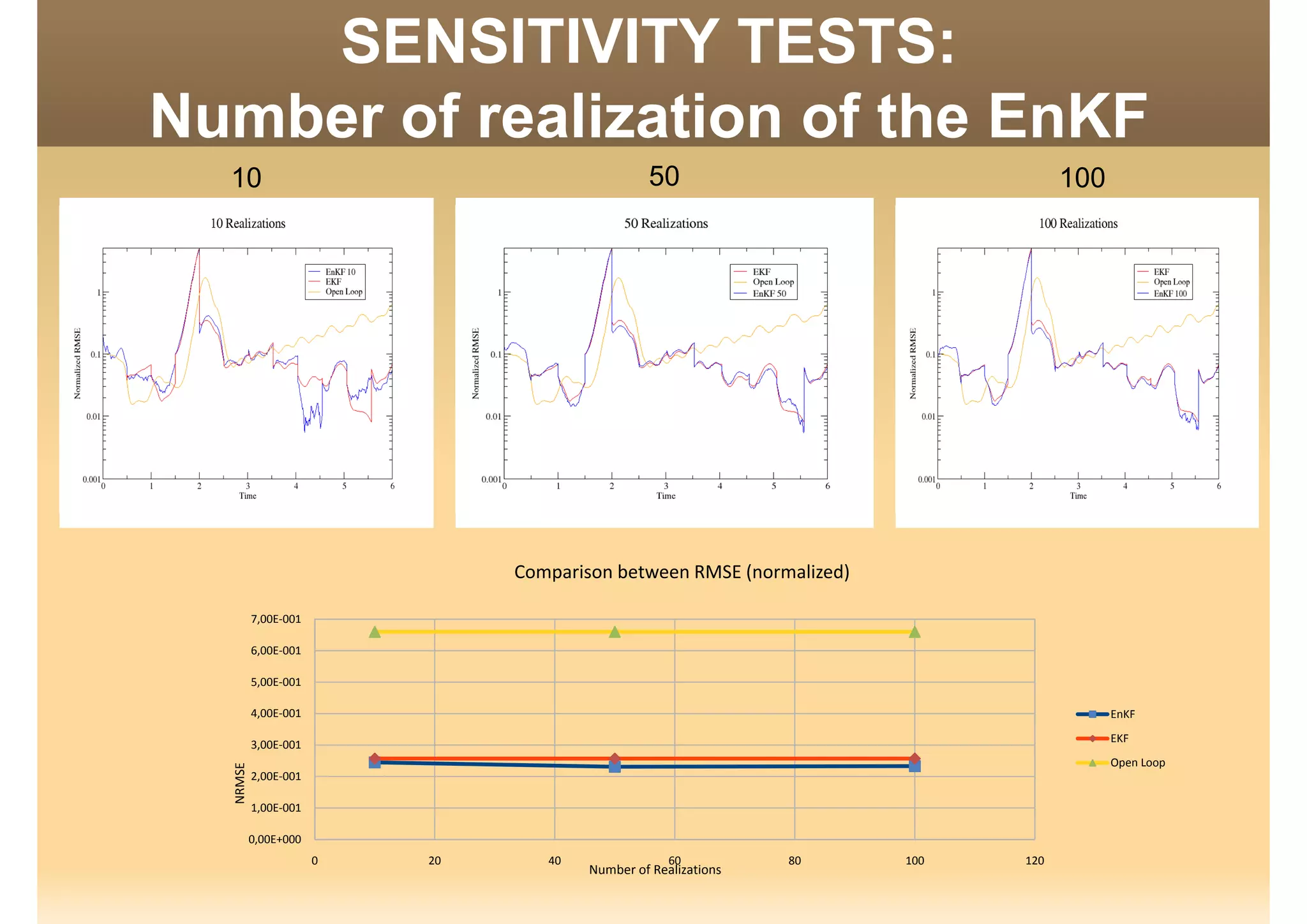
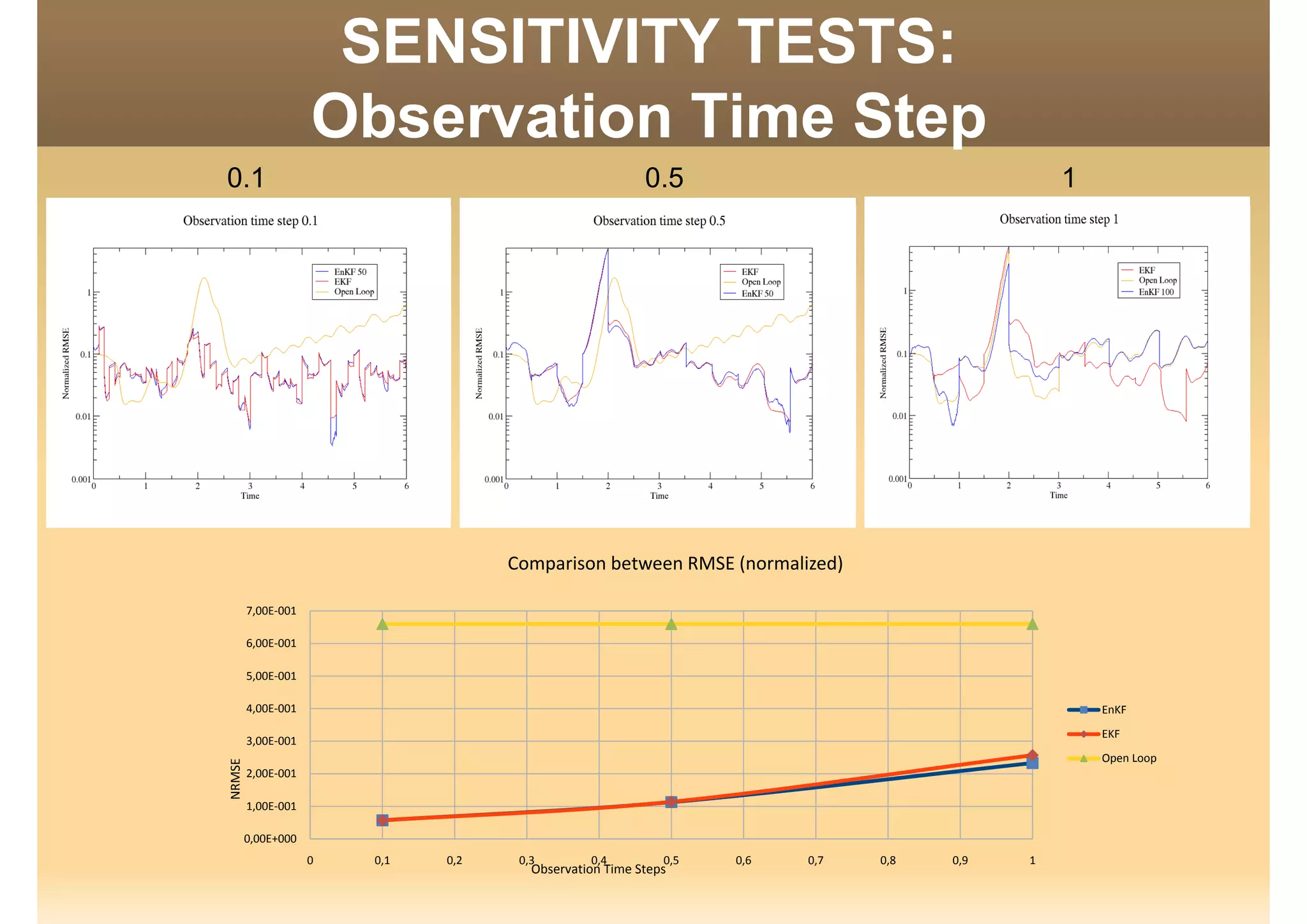
The document discusses the application of data assimilation techniques, specifically Ensemble Kalman Filter (EnKF) and Extended Kalman Filter (EKF), to the Lorenz model, which simulates thermal convection in the atmosphere. Sensitivity tests demonstrate that a realization number of 10 is optimal for the model, and that error rates increase with fewer observations. The authors suggest using these methods for real-world problems, such as weather prediction, while emphasizing future challenges in the field.

1. Biogeodynamics and Earth System
Sciences Summer School (BESS)Sciences Summer School (BESS)
Data Assimilation for the Lorenz
(1963) Model using Ensemble
d E t d d K l Filtand Extended Kalman Filter
D. Pasetto (a) and C. Vitolo (b)
Advisor M.Ghil, ENS & UCLA
(a) Universita' di Padova (Italy)
(b) Imperial College London (UK)

2. Data Assimilation for the Lorenz model using
Ensemble and Extended Kalman FilterEnsemble and Extended Kalman Filter
OUTLINE
Data AssimilationData Assimilation
Kalman Filter (EnKF and EKF)
Lorenz ModelLorenz Model
Results of Sensitivity Tests
Future Challenges

3. DATA ASSIMILATIONSS O
Data Assimilation is usually defined as
”Estimation and prediction (analysis) of an unknown trueEstimation and prediction (analysis) of an unknown true
state by combining observations and system dynamics
(model output)”( p )
It is needed in order to:
- Reduce uncertainties and biases
- Improve forecasting
- Estimate initial state of a system (e g hydrologic system)Estimate initial state of a system (e.g. hydrologic system)
from multiple sources of information
- Permit forecast adjustmentsPermit forecast adjustments

4. EXAMPLE
Lorenz's Model
a simplified model of thermal convectiona simplified model of thermal convection
in the atmosphere.
Outcome:
- No predictable
pattern
- Butterfly effect

5. A BIT OF MATHS...O S
The Lorenz model
Bistability and
chaotic behaviour
Where:
For the bistable behaviour:Matlab code to simulate For the bistable behaviour:
 = 8/3,  =1.01,  = 10
For the Lorenz attractor:
Matlab code to simulate
the model dynamics
Perturbation of a ”true run”
 = 8/3,  =28,  = 10
Perturbation of a true run
with a random noise to get
”pseudo-observations”p

6. A BIT MORE MATHSO S
Kalman FilterKalman Filter
Data assimilation in non linear models: EKF, EnKF and Particle Filters

7. RESULTS

8. RESULTS

9. RESULTS

10. RESULTS

11. SENSITIVITY TESTS:
N b f li ti f th E KFNumber of realization of the EnKF
10 50 100
7 00E 001
Comparison between RMSE (normalized)
4,00E‐001
5,00E‐001
6,00E‐001
7,00E‐001
EnKF
1,00E‐001
2,00E‐001
3,00E‐001
,
NRMSE
EKF
Open Loop
0 20 40 60 80 100 120
0,00E+000
Number of Realizations

12. SENSITIVITY TESTS:
Ob ti Ti StObservation Time Step
0.1 0.5 1
7,00E‐001
Comparison between RMSE (normalized)
4,00E‐001
5,00E‐001
6,00E‐001
,
EnKF
1,00E‐001
2,00E‐001
3,00E‐001
NRMSE
EKF
Open Loop
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
0,00E+000
Observation Time Steps

13. CONCLUSIONSCO C US O S
Data Assimilation on the Lorenz Model using EnKF
and EKF was performed:and EKF was performed:
Sensitivity tests on the number of realization on the
EnKF show that N=10 is already optimal for this
small model
Sensitivity tests on the observation time steps
sho the error increases as the amo nt ofshow the error increases as the amount of
information provided decreases
EnKF and EKF perform similarly but EKF is to be
prefered because computationally more efficientprefered because computationally more efficient

14. FUTURE CHALLENGESU U C G S
Further sensitivity tests
(e.g. ”bistable dynamics”)
Parameter estimationParameter estimation
Utilize Data Assimilation for ”real
problems” (e.g. Weather predictions)

15. Data Assimilation for the Lorenz model using
Ensemble and Extended Kalman FilterEnsemble and Extended Kalman Filter
Thanks for your attentionThanks for your attention