This document discusses the analysis of balanced and unbalanced faults in power systems. It introduces balanced three-phase faults and various types of unbalanced faults. The key aspects covered include: - Determining bus voltages and line currents during different fault types for protection and rating equipment. - Generator behavior during sub-transient, transient, and steady-state periods of a fault. - Calculating fault current, bus voltages, and line currents using bus impedance matrix methods for examples of three-phase faults on different buses. - Definitions and calculations related to short-circuit capacity and symmetrical components analysis for unbalanced faults.

1. BEF43303
POWER SYSTEM ANALYSIS AND PROTECTION
ANALYSIS OF BALANCED AND UNBALANCED FAULTS
WEEK 4

2. 4.0 CONTENTS
4.1 Introduction
4.2 Balanced three-phase fault
4.3 Short-circuit capacity
4.4 Fundamental of symmetrical components

3. 4.1 INTRODUCTION
• Important part of power system analysis.
• Determining of bus voltages and line currents during various types
of faults.
• The fault types are segregated as follows:
 Balanced three-phase fault.
 Unbalanced faults:
• Single line to ground fault,
• Line-to-line fault,
• Double line to ground fault.

4. 4.1 INTRODUCTION
• It is used for proper relay setting and coordination.
• The three-phase balanced fault information is used to select and set
phase relays.
• The line-to-ground fault is used for ground relays.
• It is also used to obtain the rating of the protective switchgears.
• The magnitude of the fault currents depends on:
 The internal impedance of the generators,
 The impedance of the intervening circuit.

5. 4.1 INTRODUCTION
• The generator behavior can be divided into three periods:
 The sub-transient period
• Represented by sub-transient reactances 𝑋′′𝑑.
• Lasting only for the first few cycles.
 The transient period
• Represented by transient reactances 𝑋′𝑑.
• Covering a relatively longer time.
 The steady state period
• Represented by synchronous reactance 𝑋𝑑.
• For steady state condition.

6. 4.2 BALANCED THREE-PHASE FAULT
• The duration of the short circuit current depends on the time of
operation of the protective system.
• Generally, the subtransient reactance is used for determining the
interrupting capacity of the circuit breakers.
• For relay setting and coordination, fault studies required transient
reactance.
• Also, transient reactance is used in transient stability.

7. 4.2 BALANCED THREE-PHASE FAULT
Example 4.1
The one-line diagram of a simple three-bus power system is shown in
Figure 1. Each generator is represented by an emf behind the transient
reactance. All impedances are expressed in per unit on a common 100
MVA base, and for simplicity, resistances are neglected. The following
assumptions are made.
i. Shunt capacitances are neglected and the system is considered on
no-load.
ii. All generators are running at their rated voltage and rated
frequency with their emfs in phase.

8. 4.2 BALANCED THREE-PHASE FAULT
Example 4.1 Determine the fault current, the
bus voltages, and the line currents
during the fault when a balanced
three-phase fault with a fault
impedance 𝑍_𝑓= 0.16 per unit
occurs on:
a) Bus 3 [-j2.0 pu, -j0.1 pu, -j1.1 pu, -
j0.9 pu],
b) Bus 2 [-j2.5 pu, -j0.5 pu, -j0.5 pu, -
j0.5 pu],
c) Bus 1 [j3.125 pu, j3.125 pu, -j3.125
pu, -j3.125 pu].
Figure 1

9. 4.2 BALANCED THREE-PHASE FAULT
Example 4.2
A three-phase fault with a fault impedance 𝑍𝑓 = 0.16 per unit occurs at
bus 3 in the network of Example 4.1. Using the bus impedance matrix
method, compute the fault current, the bus voltages, and the line
currents during the fault.

10. 4.2 BALANCED THREE-PHASE FAULT
Tutorial 4.1
A three-phase fault with a fault impedance 𝑍𝑓 = 0.16 per unit occurs at
bus 3 in the network of Example 4.1. Using the bus impedance matrix
method, compute the fault current, the bus voltages, and the line
currents during the fault.

11. 4.2 BALANCED THREE-PHASE FAULT
• The load currents were neglected and all prefault bus voltages were
assumed to be equal to 1.0 per unit.
• For more accurate calculation, the prefault bus voltages can be
obtained from the power flow solution.
• In a power system, loads are specified and the currents are
unknown.
• Express the loads by a constant impedance evaluated at the prefault
bus voltages.
• This is a very good approximation which results in linear nodal
equations.

12. 4.3 SHORT-CIRCUIT CAPACITY
• It is a common measure of the strength of a bus.
• Definition: The product of the magnitudes of the rated bus voltage
and the fault current.
• It is used to determine the dimension of a bus bar, and the
interrupting capacity of a circuit breaker.
• The short -circuit capacity at bus k is given by:
• The line-to-line voltage 𝑉𝐿𝑘
is expressed in kilovolts and 𝐼𝑘(𝐹) is
expressed in amperes .

13. 4.3 SHORT-CIRCUIT CAPACITY
• The symmetrical three-phase fault current in per unit is given by:
• 𝑉𝑘(0) is the per unit prefault bus voltage, and 𝑋𝑘𝑘 is the per unit
reactance to the point of fault.
• System resistance is neglected.
• The base current is given by:

14. 4.3 SHORT-CIRCUIT CAPACITY
• 𝑆𝐵 is the base MVA and 𝑉𝐵 is the line-to-line base voltage in
kilovolts.
• The fault current in amperes is:
• Therefore, SCC is rewritten as follows:

15. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
• In three-phase system, the phase sequence is defined as the order in
which they pass through a positive maximum.
• Consider the phasor representation of a three-phase balanced
current shown as follows:
Figure 2

16. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
• By convention. the direction of rotation of the phasors is taken to be
counterclockwise.
• The three phasors are written as:
• 𝑎 that causes a counterclockwise rotation of 120°, such that:

17. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
• The order of the phasors is 𝑎𝑏𝑐. This is designated the positive phase
sequence.
• When the order is 𝑎𝑐𝑏, it is designated the negative phase sequence.
• The negative phase sequence quantities are represented as:
• Zero phase sequence currents, would be designated

18. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
• The order of the phasors is 𝑎𝑏𝑐. This is designated the positive phase
sequence.
• When the order is 𝑎𝑐𝑏, it is designated the negative phase sequence.
• The negative phase sequence quantities are represented as:
• Zero phase sequence currents, would be designated

19. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
• For the three-phase unbalanced currents 𝐼𝑎, 𝐼𝑏, and 𝐼𝑐, the three
symmetrical components of the current are:
• Rewrite all equations in terms of phase a components:

20. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
• In matrix notation:
• A is known as symmetrical components transformation matrix.
• The symmetrical components are:

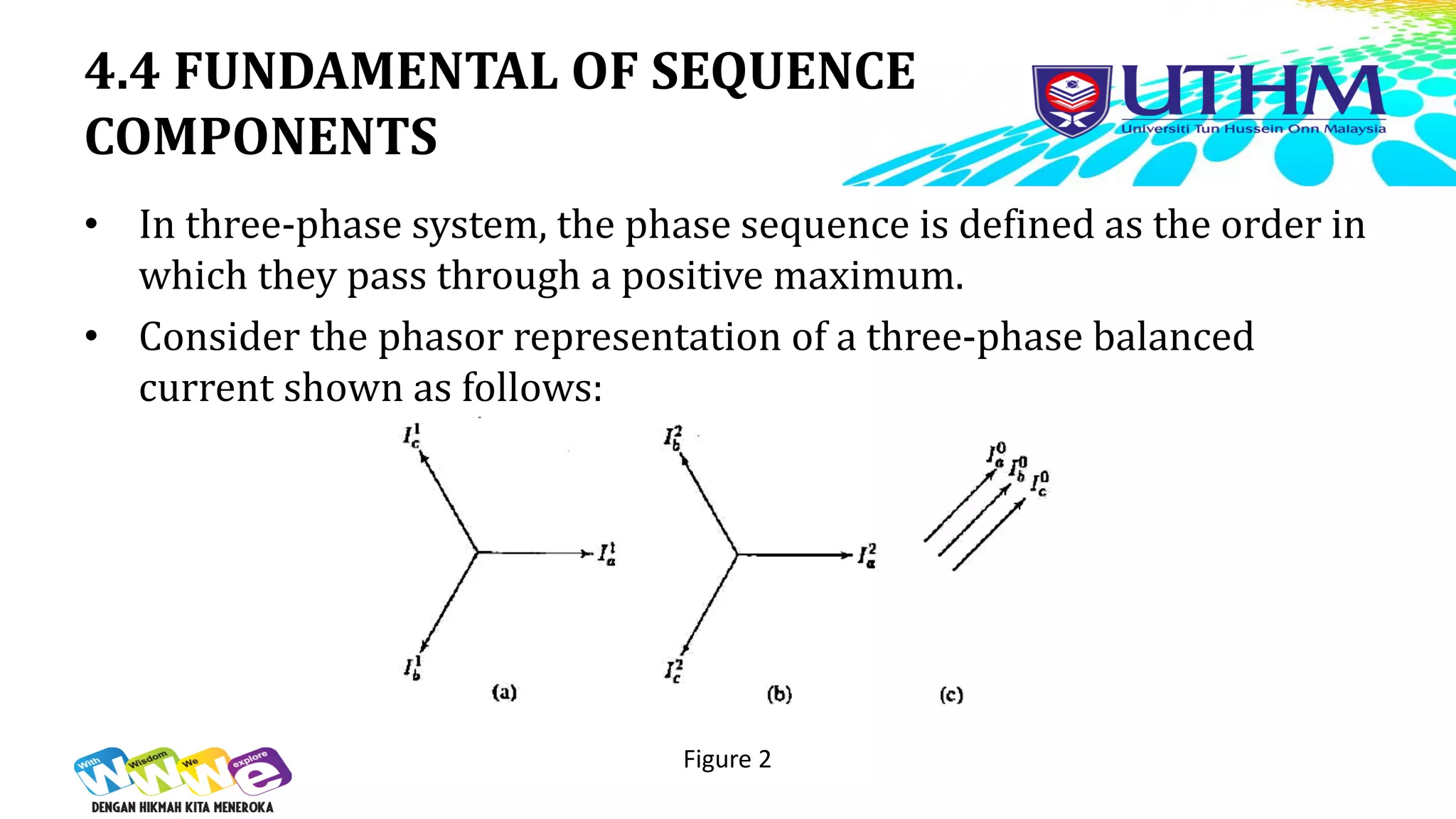
21. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
Example 4.3
Obtain the symmetrical components of a set of unbalanced currents
𝐼𝑎 = 1.6∠25°, 𝐼𝑏 = 1.0∠180°, and 𝐼𝑐 = 0.9∠132°.
[0.4512∠96.4529°
,0.9435∠ −0.0550°
,0.6024∠22.3157°
].

22. 4.4 FUNDAMENTAL OF SEQUENCE
COMPONENTS
Example 4.4
The symmetrical components of a set of unbalanced three-phase
voltages are 𝑉
𝑎
0 = 0.6∠90°, 𝑉
𝑎
2 = 1.0∠30°, and 𝑉
𝑎
1 = 0.8∠ −30°. Obtain
the original unbalanced phasors.
Obtain the symmetrical components of a set of unbalanced currents
𝐼𝑎 = 1.6∠25°, 𝐼𝑏 = 1.0∠180°, and 𝐼𝑐 = 0.9∠132°. [1.7088∠24.1825°
,
0.400∠90.0000°
, 1.7088∠155.8175°
].