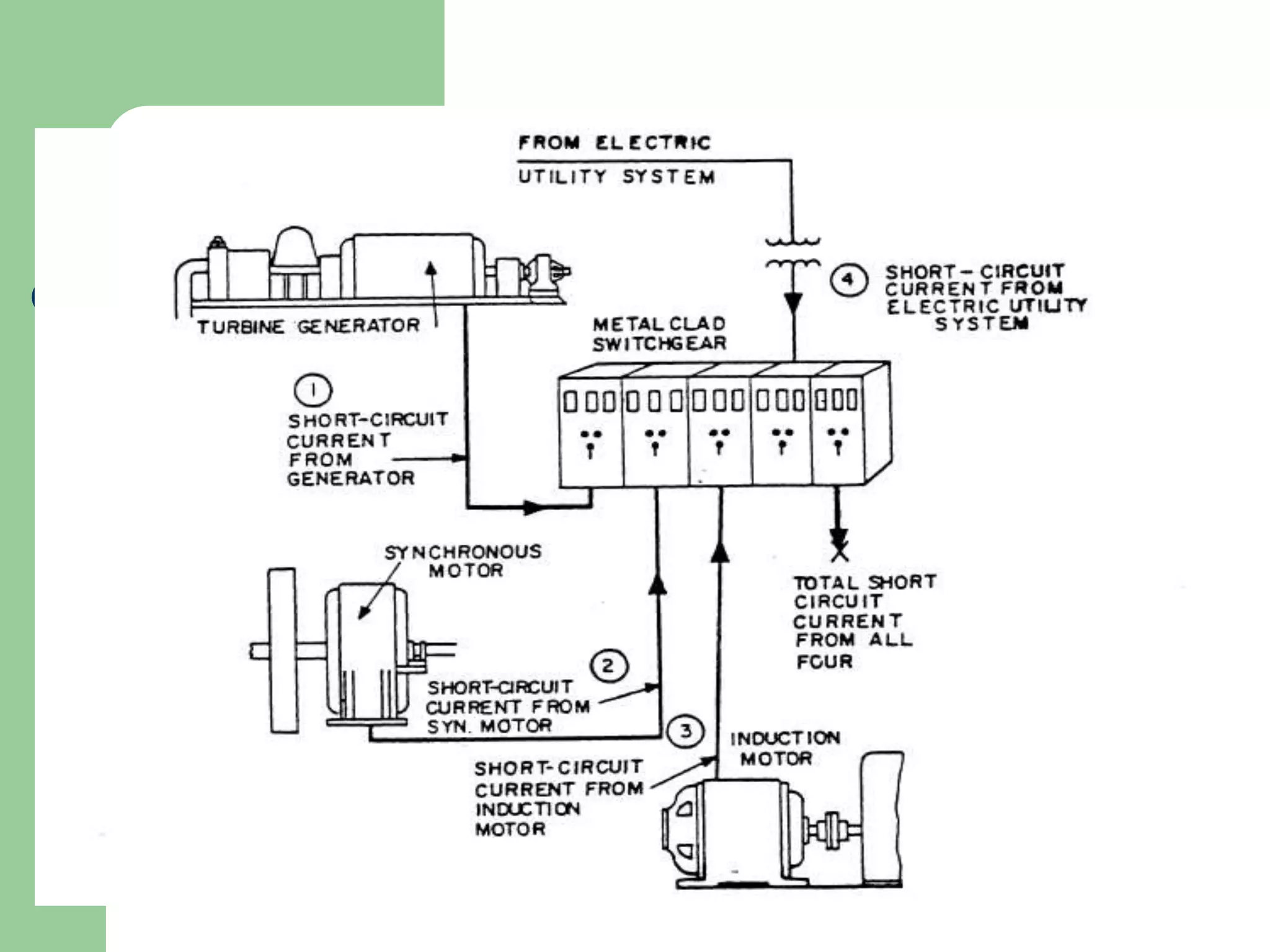
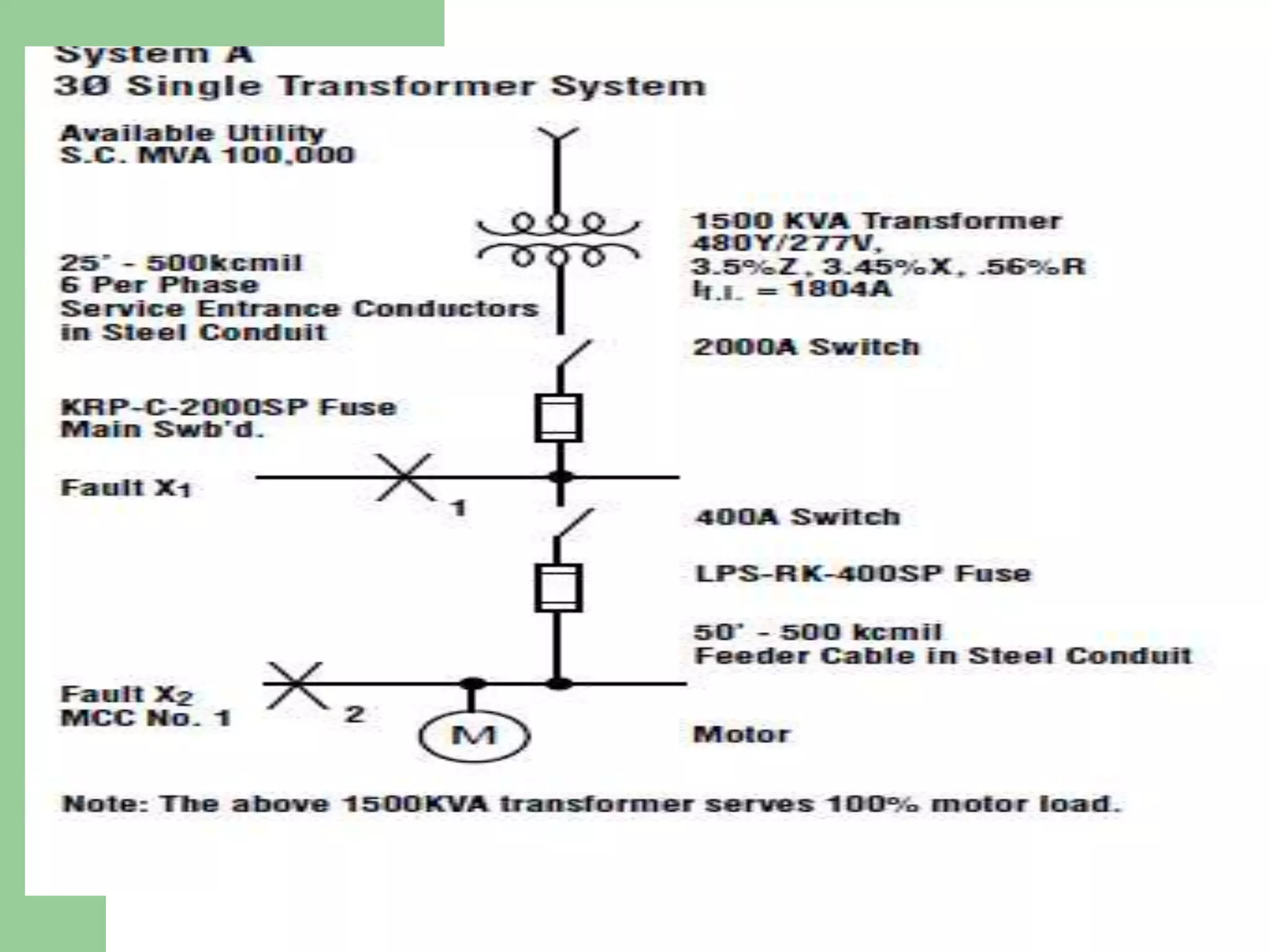
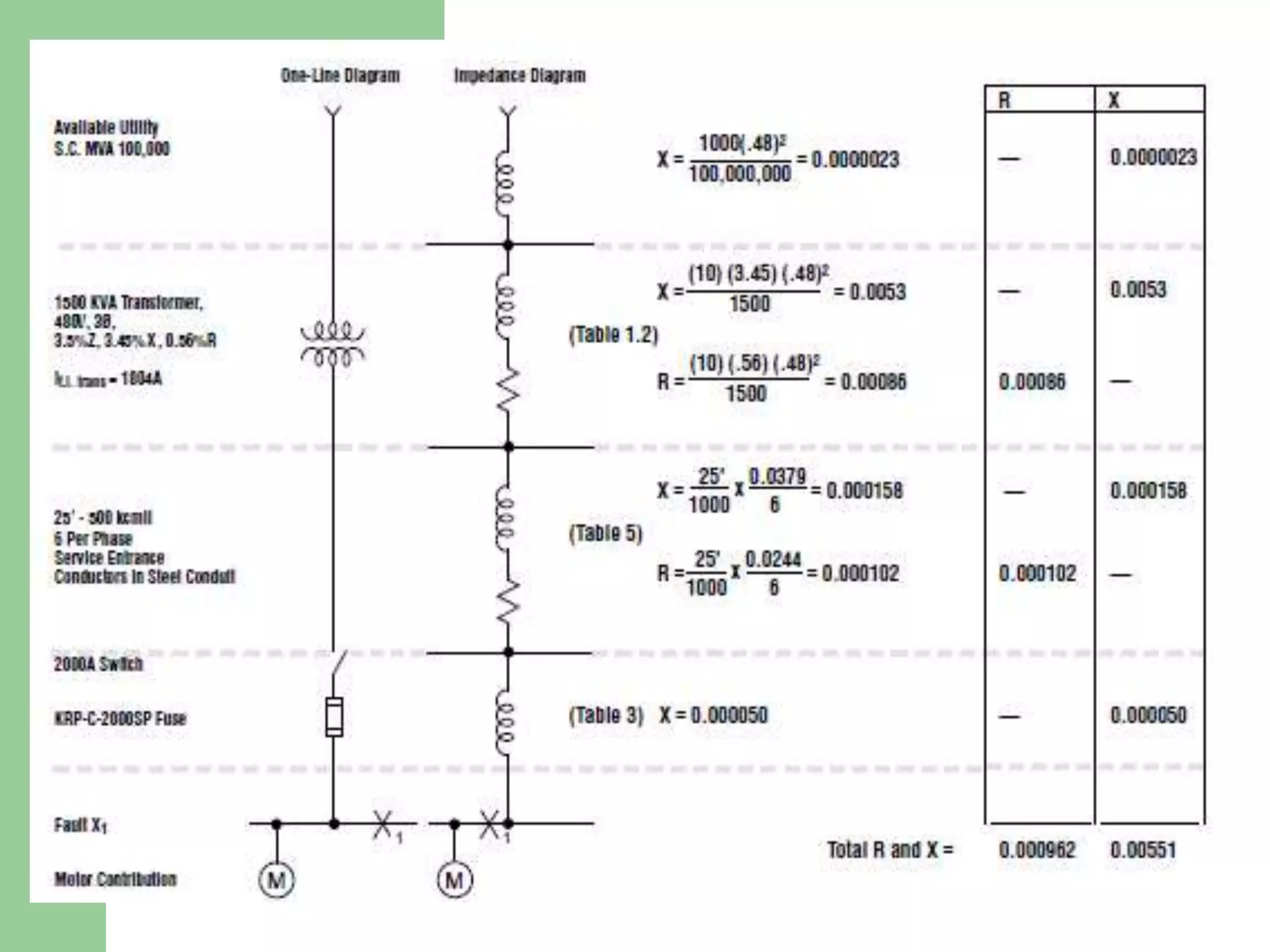
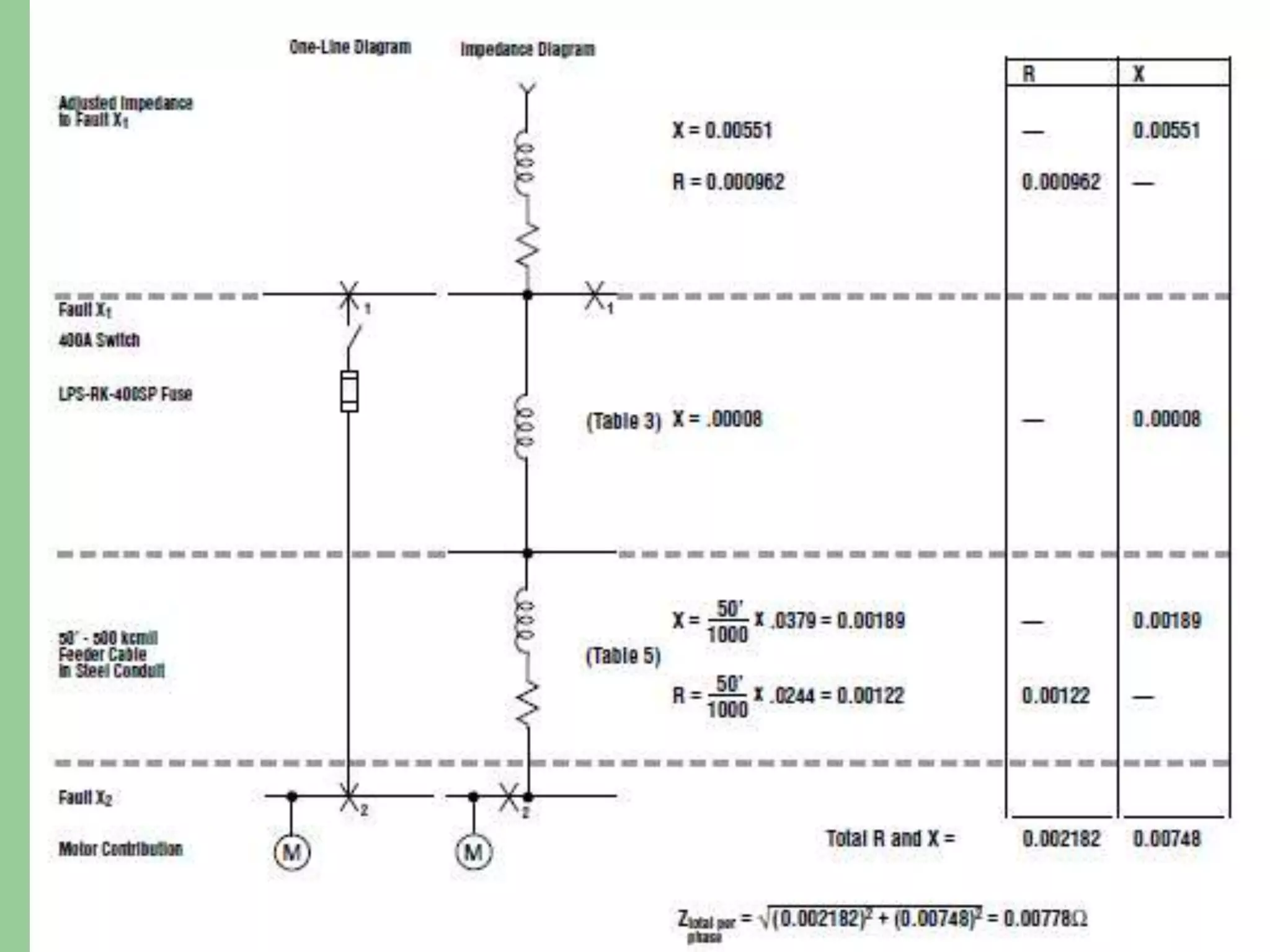
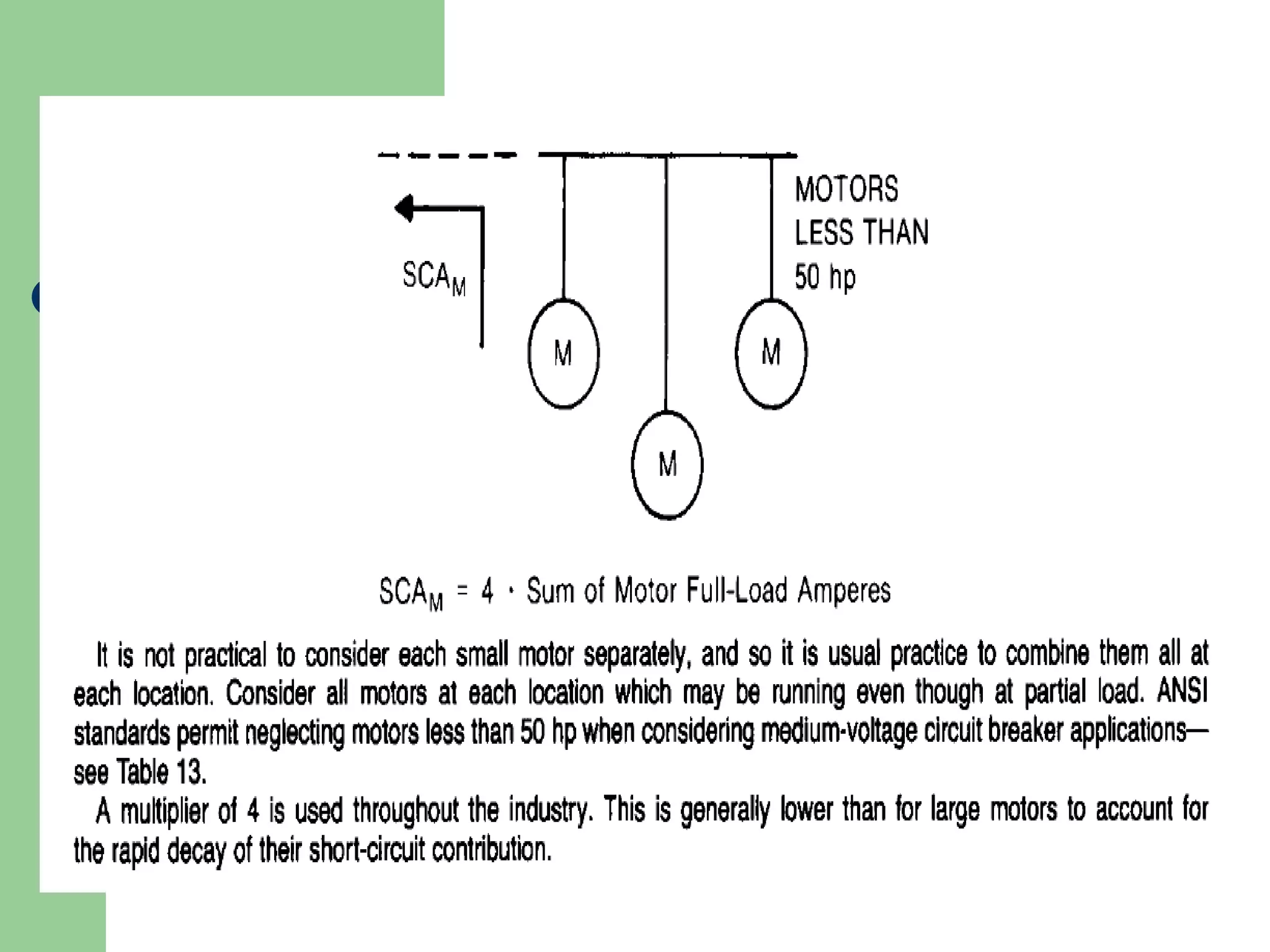
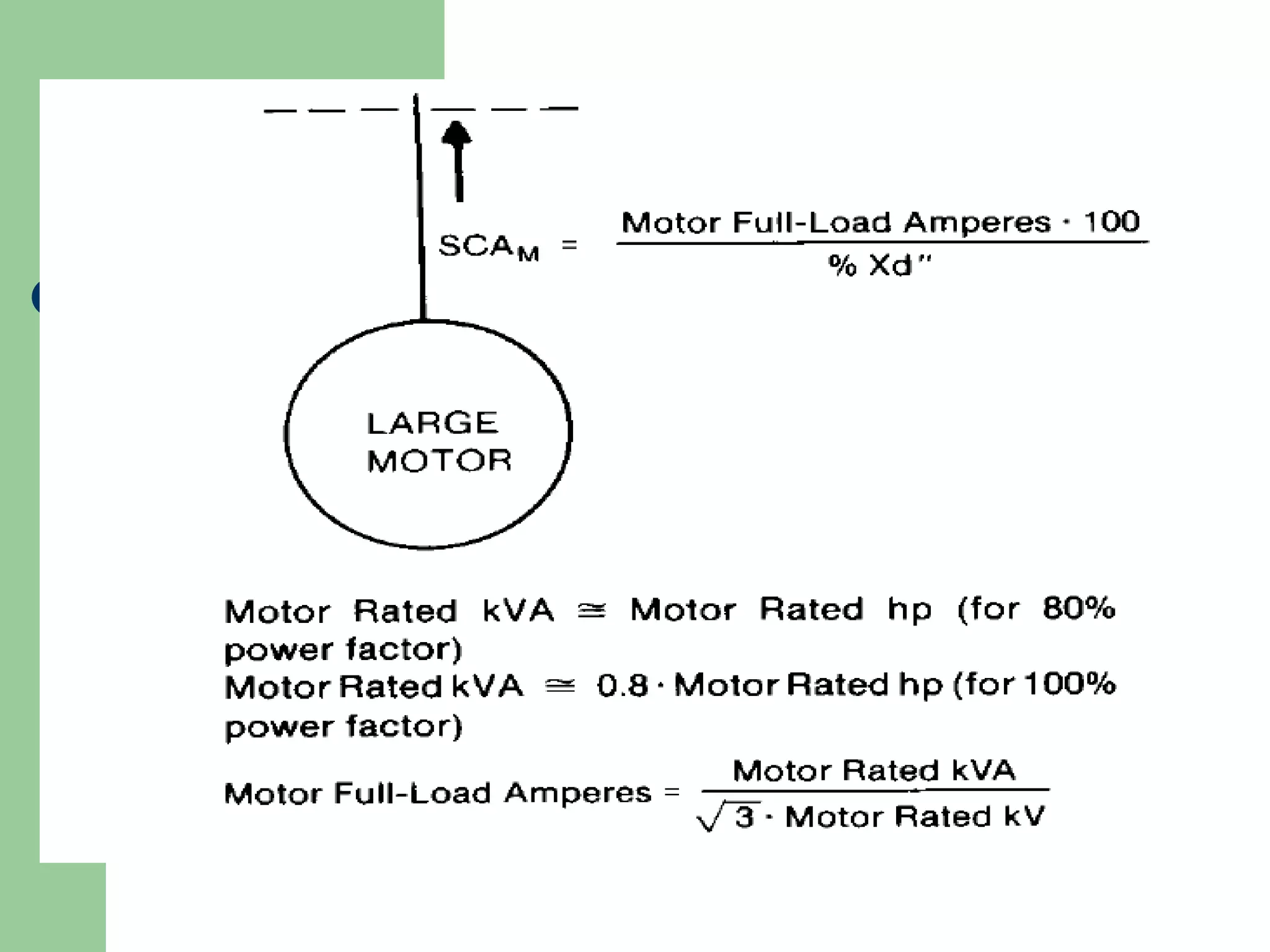
- Any abnormal condition that causes excessive current flow through unintended paths in a power system is defined as a fault. - Faults can be caused by insulation failures, lightning strikes, or accidental operations and must be safely disconnected to prevent equipment damage. - Short circuit current calculations are required to select properly rated circuit breakers and relay settings for protection schemes. 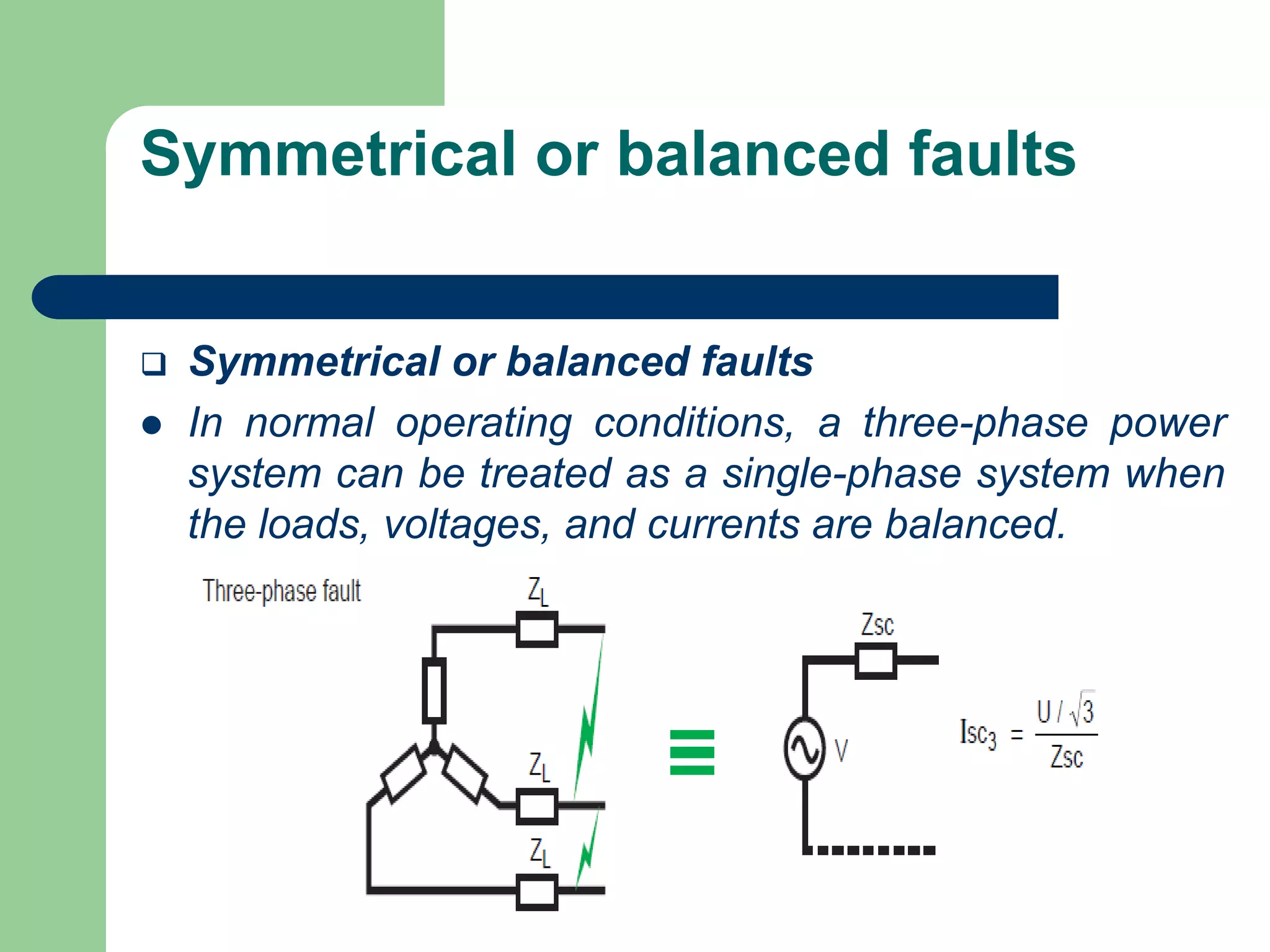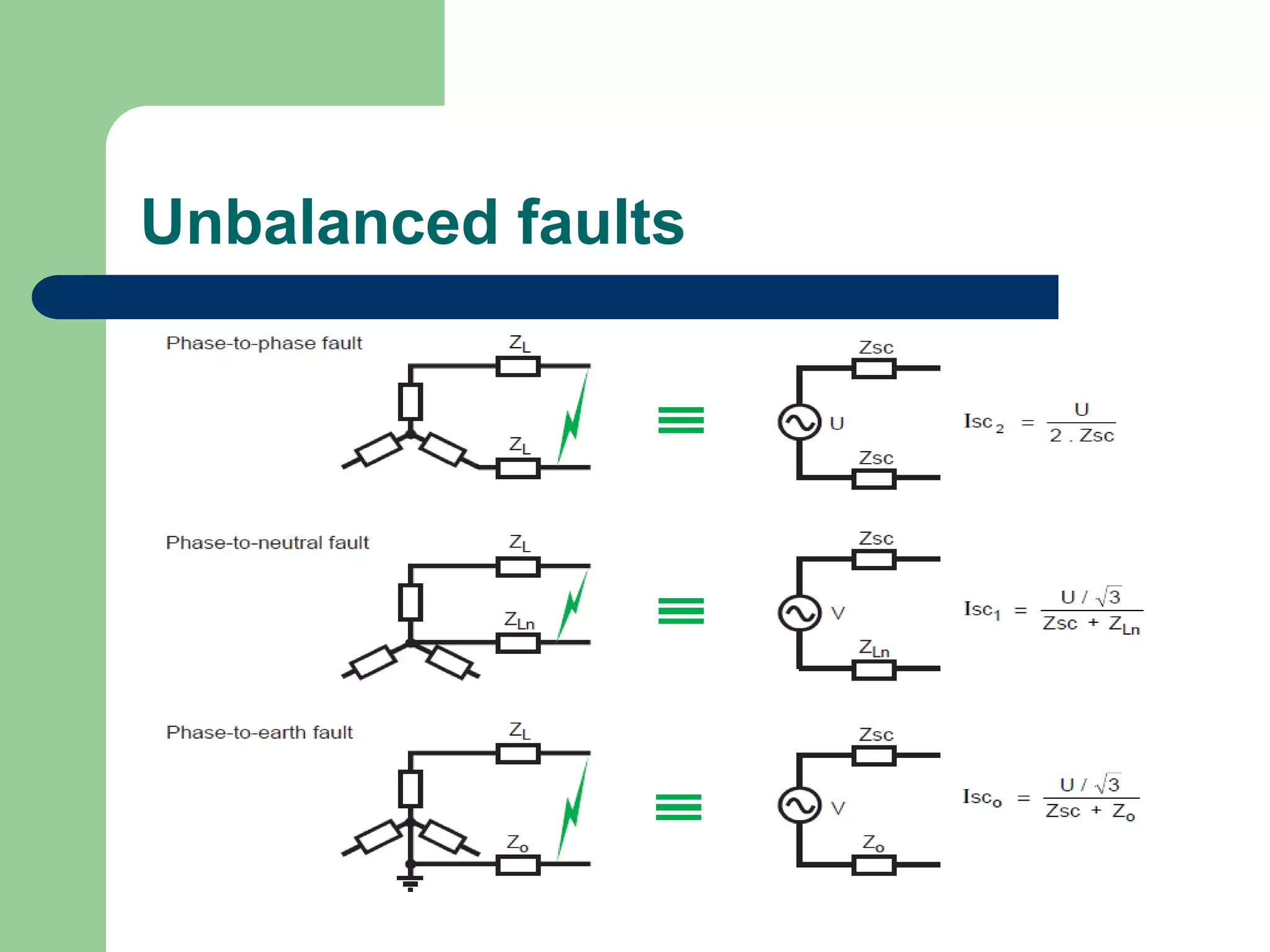- Faults are classified by nature, participating phases, and whether they are symmetrical or asymmetrical. Symmetrical faults can be analyzed using positive sequence networks while unsymmetrical faults require symmetrical component analysis.

1. POWER SYSTEM
FAULTS

4. Introduction
 Any abnormal conditions which causes flow of huge
current in the conductors or cable through inappropriate
paths in the circuit can be defined as a fault. In normal
operating conditions all the circuit elements of an
electrical system carry currents whose magnitude
depends upon the value of the generator voltage and
the effective impedances of all the power transmission
and distribution system elements including the
impedances of the loads usually relatively larger than
other impedances.

5. Introduction
 Modern electric systems may be of great complexity
and spread over large geographical area. An electric
power system consists of generators, transformers,
transmission lines and consumer equipment.. The
system must be protected against flow of heavy short
circuit currents, which can cause permanent damage
to major equipments, by disconnecting the faulty
section of system by means of circuit breaker and
protective relaying

6.  Such conditions are caused in the system accidentally
through insulation failure of equipment or flashover of
lines initiated by a lightning stroke or through accidental
faulty operation.
 The safe disconnection can only be guaranteed if the
current does not exceed the capability of the circuit
breaker. Therefore, the short circuit currents in the
network must be computed and compared with the
ratings of the circuit breakers at regular intervals as part
of the normal operation planning.

7. Introduction
 The short circuit currents in an AC system are
determined mainly by the reactance of the alternators,
transformers and lines upto the point of the fault in the
case of phase to phase faults. When the fault is
between phase and earth, the resistance of the earth
path play an important role in limiting the currents.

8. Introduction
 Balanced three phase faults may be analyzed using an
equivalent single phase circuit. With asymmetrical
three phase faults, the use of symmetrical components
help to reduce the complexity of the calculations as
transmission lines and components are by and large
symmetrical, although the fault may be asymmetrical.
Fault analysis is usually carried out in per-unit
quantities as they give solutions which are somewhat
consistent over different voltage and power ratings,
and operate on values of the order of unity.

9. Introduction
 Depending on the location, the type, the duration, and
the system grounding, short circuits may lead to
• electromagnetic interference with conductors in the
vicinity (disturbance of communication lines),
• stability problems,
• mechanical and thermal stress (i.e. damage of
equipment, and or personnel

10. Fault Types
The fault can be classified due to the NATURE of the
fault as
1- Permanent
2- Transient
Or due to PARTICIPATED PHASES as
1- Phase-Earth
2- Phase-Phase
3- Phase-Phase-Earth
4- Three-Phase or Three-Phase-Earth

11. Fault Types
Fault may be categorized broadly into 2 types:
 Symmetrical or balanced faults
 Asymmetrical or unbalanced faults

12. Symmetrical or balanced faults
 Symmetrical or balanced faults
 In normal operating conditions, a three-phase power
system can be treated as a single-phase system when
the loads, voltages, and currents are balanced.

13. Symmetrical or balanced faults
 A three phase fault is a condition where either (a) all
three phases of the system are short circuited to each
other, or (b) all three phase of the system are earthed.

14. Symmetrical or balanced faults
 This is in general a balanced condition, and we need to
only know the positive-sequence network to analyze
faults. Further, the single line diagram can be used, as
all three phases carry equal currents displaced by 120◦.
 The positive sequence system is that system in which
the phase or line currents or voltages attain a maximum
in the same cyclic order as those in a normal supply e.g.
assuming conventional counter clockwise rotation, then
the positive phase sequence phasors are as shown
below in the figure

15. Symmetrical or balanced faults
 The negative sequence system is that system in which
phasors still rotate anti-clockwise but attain maximum
value in the reverse order as shown in the figure. This
sequence only arises in the case of occurrence of an
unsymmetrical fault.

16. Symmetrical or balanced faults
 Typically, only 5% of the initial faults in a power
system, are three phase faults with or without earth. Of
the unbalanced faults, 80% are line-earth and 15% are
double line faults with or without earth and which can
often deteriorate to 3 phase fault. Broken conductor
faults account for the rest.
CAUSES :-
 System Energisation with Maintenance Earthing
Clamps still connected.
 1Ø Faults developing into 3Ø Faults

17. Unsymmetrical or Unbalanced
faults
Unbalanced Faults
Unbalanced Faults may be classified into
SHUNT FAULTS and SERIES FAULTS.
SHUNT FAULTS:
 Line to Ground
 Line to Line
 Line to Line to Ground

18. Unbalanced faults

19. Unbalanced faults
 Causes :
 1) Insulation Breakdown
 2) Lightning Discharges and other Overvoltages
 3) Mechanical Damage
During unbalanced faults, symmetry of system Is
lost therefore single phase representation is no
longer Valid

20. Unbalanced faults
SERIES FAULTS OR OPEN CIRCUIT:
Single Phase Open Circuit
Double Phase Open Circuit
Causes :
1) Broken Conductor
2) Operation of Fuses
3) Maloperation of Single Phase Circuit Breakers

21. Characteristics of Faults
A fault is characterized by:
 Magnitude of the fault current
 Power factor or phase angle of the fault current
The magnitude of the fault current depends upon:
 The capacity and magnitude of the generating sources
feeding into the fault
 The system impedance up to the point of fault or source
impedance behind the fault
 Type of fault
 System grounding, number and size of overhead ground
wires

22. Characteristics of Faults
 Fault resistance or resistance of the earth in the case
of ground faults and arc resistance in the case of both
phase and ground faults
The phase angle of the fault current is dependent upon:
 For phase faults: - the nature of the source and
connected circuits up to the fault location and
 For ground faults: - the type of system grounding in
addition to above.

23. Necessity for fault calculations
Fault calculations are done primarily for the following:
 To determine the maximum fault current at the point of
installation of a circuit breaker and to choose a
standard rating for the circuit breaker (rupturing)
 To select the type of circuit breaker depending upon
the nature and type of fault.

24. Necessity for fault calculations
 To determine the type of protection scheme to be
deployed.
 To select the appropriate relay settings of the
protection scheme.
 To co-ordinate the relay settings in the overall
protection scheme of the system

25. Procedures and Methods
 To determine the fault current at any point in the
system, first draw a one-line diagram showing all of the
sources of short-circuit current feeding into the fault, as
well as the impedances of the circuit components.
 To begin the study, the system components, including
those of the utility system, are represented as
impedances in the diagram.

26. Procedures and Methods
 It must be understood that short circuit calculations are
performed without current limiting devices in the
system. Calculations are done as though these devices
are replaced with copper bars, to determine the
maximum “available” short circuit current. This is
necessary to project how the system and the current
limiting devices will perform.

28. Procedures and Methods
 To start, obtain the available short-circuit KVA, MVA, or
SCA from the local utility company.

29.  The utility estimates the System can deliver a
shortcircuit of Y MVA at the primary of the
transformer. Since the X/R ratio of the utility
system is usually quite high, only the reactance
need be considered.
 With this available short-circuit information,
begin tomake the necessary calculations to
determine the fault current at any point in the
electrical system.

34. Procedures and Methods
The calculation is not only limited to present system
requirements but also meet:
 The future expansion schemes of the system such as
addition of new generating units
 Construction of new transmission lines to evacuate
power.
 Construction of new lines to meet the load growth and
or Construction of interconnecting tie lines

35. Procedures and Methods
Basically, there are two approaches to fault
calculations. These are:
(a) Actual reactance or impedance method
(b) Percentage reactance or impedance method or per
unit (p.u) reactance or impedance method.
 Machine and Transformer impedance or reactance are
always noted in percentage values on the nameplate.
Hence the latter method is considered for our
calculation.

36. Per Unit and Percentage
System
Definitions
 The per unit value is defined as the ratio of the actual
quantity to a reference quantity which is often referred
to as base quantity. The base quantity is an arbitrary or
convenient reference value but of the same unit as the
actual value.
i.e. per unit = Actual quantity
Base quantity(value),

37. Per Unit and Percentage System
formulae
 Both the actual and base quantities can be scalar or
complex value but should be of the same units e.g
Amps, Ohms, Watts, Vars and VA. The per unit values
are therefore scalar quantities i.e. non- dimensional.

38. Per Unit and Percentage System
formulae
Base value
For a three phase power system, let Ib, KVb and MVAb
be the base current, line voltage and power respectively.
The base impedance, Zb = KVb
√3 x Ib
The base MVA, MVAb = √3 x Ib x KVb
= √3 x KVb x KVb
√3 x Zb
Zb = (KVb)2
MVAb

39. Per unit
 Let Z be the actual impedance in ohms,
Z per unit(pu) = Z
Zb
= Z x MVAb
(KVb)2
Changing of base
Let Ib1, KVb1 and MVAb1 be the old base values and
Ib2, KVb2 and MVAb2 the new base values.

40. Per unit
Z1(pu) = Z x MVAb1
(KVb1)2
where; Z = actual value and
Zb = (KVb1)2
MVAB1
therefore,
Z = Z1(pu) x MVAB1
(KVb1)2
Z2(pu) = Z x MVAb2
(KVb2)2

41. Per unit
Z2(pu) = = Z1(pu) x (KVb1) 2 x MVAb2
MVAB1 (KVb2)2
1) If KVb1 = KVb2 then, Z2(pu) = Z1(pu) MVAb2
MVAb1
2) If MVAb1 = MVAb2 then, Z2(pu) = Z1(pu) (KVb1) 2
(KVb2)2

42. Examples
Example1
(1) To calculate the p.u impedance and % impedance of
a transmission line at 100 MVA
base Line voltage 330 KV
Line length 200 Kms
Line resistance /Km = 0.06 ohms/Km
Line reactance /Km = 0.4 ohms/Km

43. Examples
Z = R + jX
For the 200kms line length
Z = 200 (0.06 + j 0.4)
= 12 + j 80
|Z| =  [(12) 2 + (80) 2] = 80.895 ohms

44. Examples
Zp.u = Z x MVA base
(KV) 2 base
= 80.895 x 100
(330) 2
= 0.0743 p.u
%Z = 0.074 x 100
= 7.43

45. Examples
Example2
To calculate the p.u impedance to a 100 MVA base
Given four generators; 90MVA, 11KV of 15%
impedance each connected to step up transformers of
90MVA 11KV/330KV of 14% impedance. Calculate the
fault current at F.

46. Examples
Assumed MVA = 100
%Z generators = 15 on 90 MVA base
or Zg p.u = 0.15 on 90 MVA base
Zg p.u on 100 MVA base will be:
(Zg p.u) base2 = (Zg p.u) base1 x MVA base2
MVA base1
(Zg p.u) 100 = 0.15 x 100
90
= 0.167

47. Examples
%Z transformers = 14 on 90 MVA base
or Zt p.u = 0.14 on 90 MVA base
Zt p.u on 100 MVA base will be:
(Zt p.u) base2 = (Zt p.u) base1 x MVA base2
MVA base1
(Zt p.u) 100 = 0.14 x 100
90
= 0.156

48. Examples
The system reduces as follows

49. Examples
Ztotal = 0.323
4
= 0.08075
Total p.u impedance at F = 0.08075 = Ztotal
Fault MVA at F = Base MVA
Ztotal
= 100 MVA
0.08075
= 1238.4 MVA

50. Examples
Current at F = Fault MVA x (10) 3
3 x system voltage (KV) at point of fault
= 1238.4 x (10) 3
3 x 330
= 2166.638Amps

51. Examples
Example2
 To calculate the fault MVA and fault current of a
system at 33KV given the fault level at the 330KV bus
as 5000MVA

52. Examples
Assume 100 MVA base
Fault MVA = Base (MVA)
Z p.u
5000 = 100
Zp.u
Z p.u = 100 = 0.02 p.u
5000 (source impedance in p.u)
Zp.u of each 330/132KV 80MVA Transformer at 100MVA base
Zp.u = 12 x 100 = 0.15
100 80

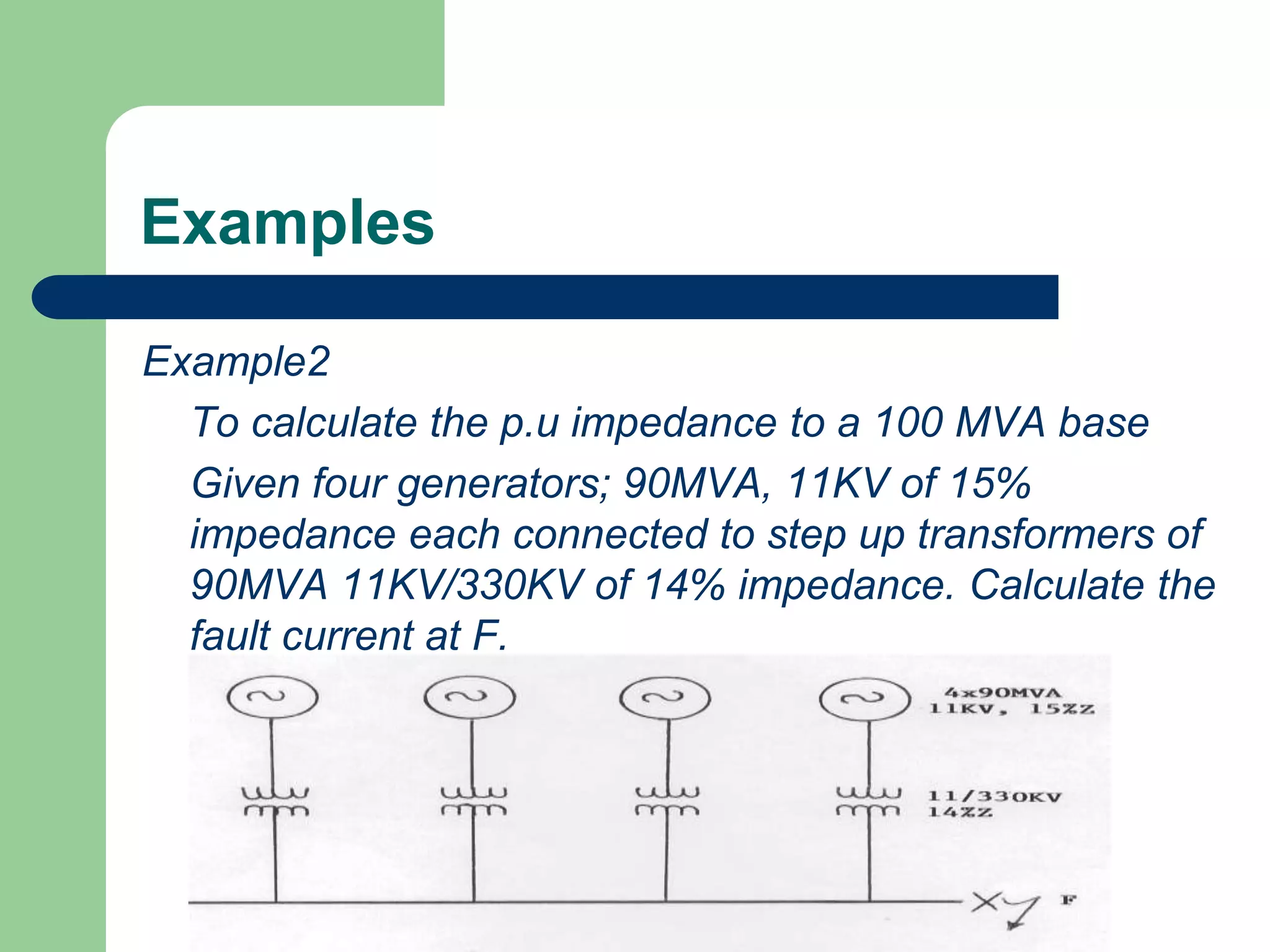
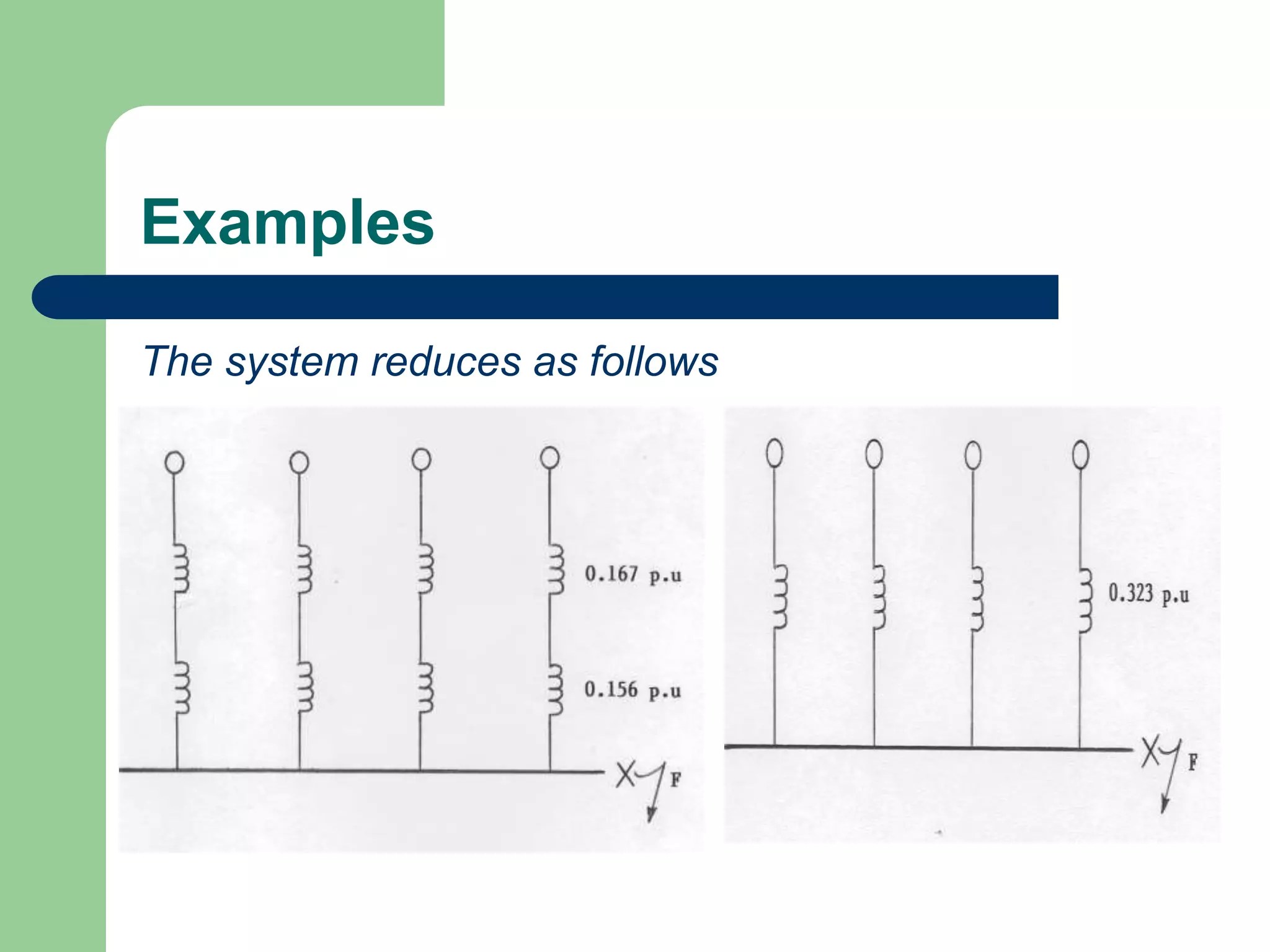
53. Examples
Z1 of 132KV Trans. line = 15 + j 60 = R + jX
= [(15) 2 + (60) 2 ]
= 61.85 0hms
Z1 p.u. of this line = (Z) MVA base
(KV) 2
= (61.85) x 100
(132) 2
= 0.355 p.u

54. Examples
Impedance of 132/33 KV, 25MVA transformer on 100
MVA base at %z =10
Zt1 = 100 x 10%
25
40%
or Zt1 = 0.4 p.u

55. Examples
 The system now reduces as follows: This can be further reduced to:

56. Examples
Total system impedance up to F
= 0.85p.u
Fault MVA at F = 100
0.85
= 117.6 MVA
 Fault current at F = 117.6 x 1000
3 x 33
= 2057.466 Amps
or 2.058 KA

57. THANK YOU FOR LISTINING