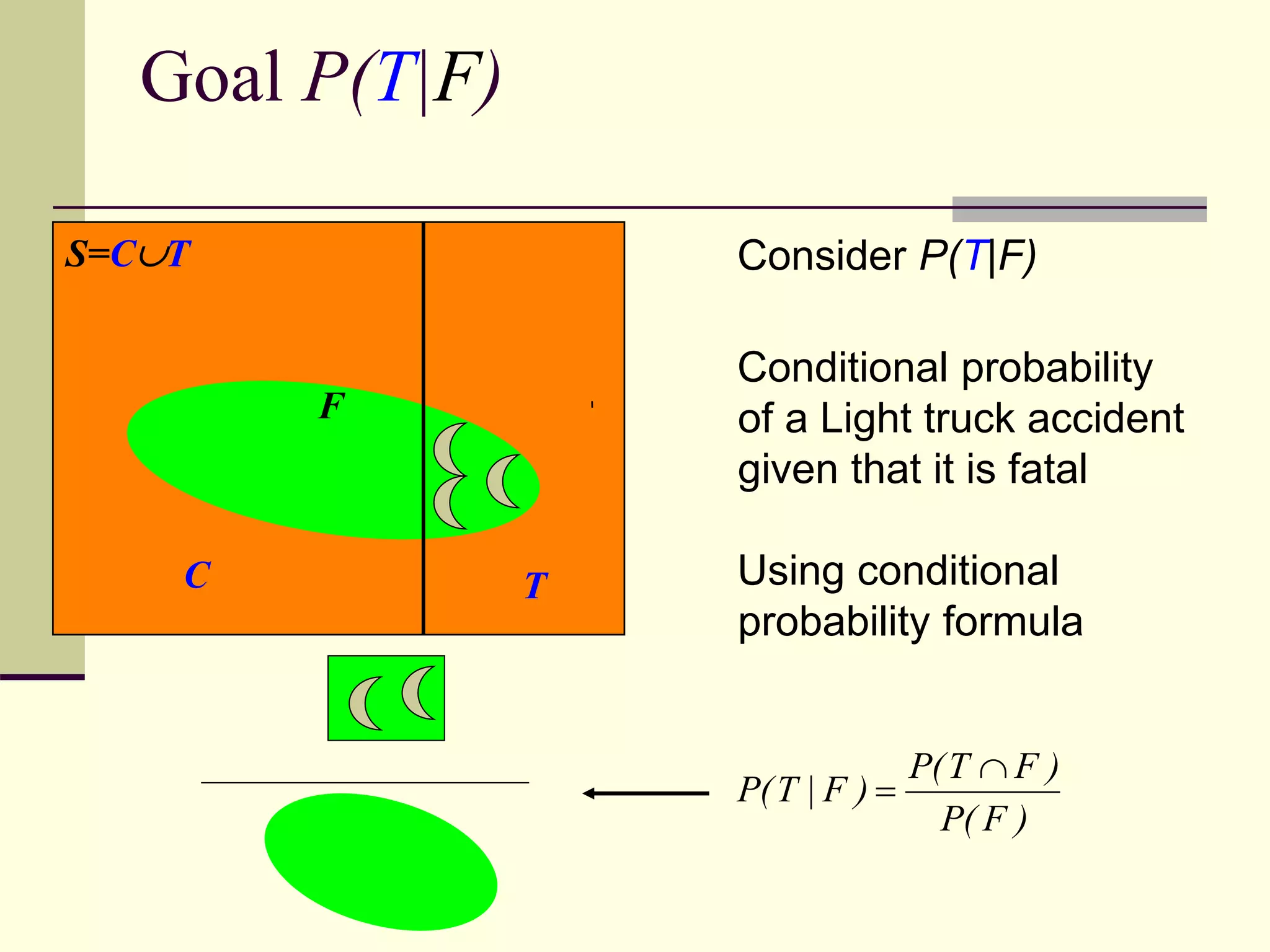
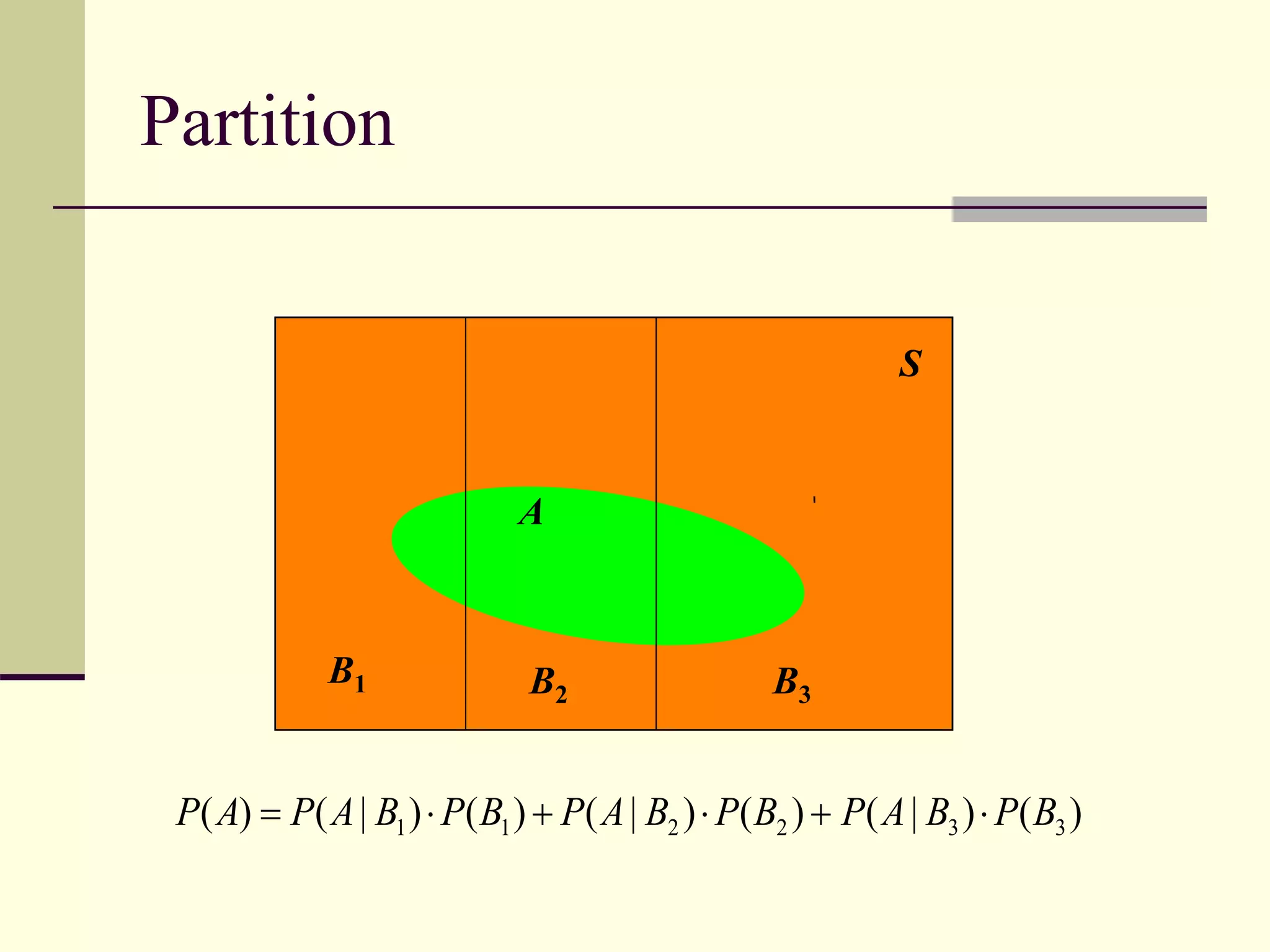
This document provides an overview of Bayes' theorem and examples of how to apply it to calculate conditional probabilities. It begins with definitions of partition, conditional probability, and the law of total probability. It then presents an example showing how to use Bayes' theorem to calculate the probability of a successful sidewalk sale given the probability of rain. Another example calculates the probability of a fatal car accident involving a light truck. The document concludes by discussing how Bayes' theorem could help calculate conditional probabilities for a loan workout decision based on new information about a borrower's years of business experience.

1. Bayes’Theorem
Special Type of Conditional Probability

2. Recall- Conditional Probability
 P(Y  T  C|S) will be used to calculate
P(S|Y  T  C)
 P(Y  T  C|F) will be used to calculate
P(F|Y  T  C)
 HOW?????
 We will learn in the next lesson?
 BAYES THEOREM

3. Definition of Partition
Let the events B1, B2, , Bn be non-empty subsets
of a sample space S for an experiment. The Bi’s
are a partition of S if the intersection of any two of
them is empty, and if their union is S. This may be
stated symbolically in the following way.
1. Bi  Bj = , unless i = j.
2. B1  B2    Bn = S.

4. Partition Example
S
B1 B2 B3

5. Example 1
Your retail business is considering holding
a sidewalk sale promotion next Saturday.
Past experience indicates that the
probability of a successful sale is 60%, if it
does not rain. This drops to 30% if it does
rain on Saturday. A phone call to the
weather bureau finds an estimated
probability of 20% for rain. What is the
probability that you have a successful
sale?

6. Example 1
Events
R- rains next Saturday
N -does not rain next Saturday.
A -sale is successful
U- sale is unsuccessful.
Given
P(A|N) = 0.6 and P(A|R) = 0.3.
P(R) = 0.2.
In addition we know R and N are complementary events
P(N)=1-P(R)=0.8
Our goal is to compute P(A).
)
R
N
( c


7. Using Venn diagram –Method1
Event A is the
disjoint union of
event R  A
&
event N  A
S=RN
R N
A
P(A) = P(R  A) + P(N  A)

8. P(A)- Probability that you have a
Successful Sale
We need P(R  A) and P(N  A)
Recall from conditional probability
P(R  A)= P(R )* P(A|R)=0.2*0.3=0.06
Similarly
P(N  A)= P(N )* P(A|N)=0.8*0.6=0.48
Using P(A) = P(R  A) + P(N  A)
=0.06+0.48=0.54

9. Let us examine P(A|R)
 Consider P(A|R)
 The conditional
probability that sale is
successful given that it
rains
 Using conditional
probability formula
)
R
(
P
)
A
R
(
P
)
R
|
A
(
P


S=RN
R N
A

10. Tree Diagram-Method 2
Bayes’, Partitions
Saturday
R
N
A R  A 0.20.3 = 0.06
A N  A 0.80.6 = 0.48
U R  U 0.20.7 = 0.14
U N  U 0.80.4 = 0.32
0.2
0.8
0.7
0.3
0.6
0.4
Probability
Conditional
Probability
Probability
Event
*Each Branch of the tree represents the intersection of two events
*The four branches represent Mutually Exclusive events
P(R ) P(A|R)
P(N ) P(A|N)

11. Method 2-Tree Diagram
Using P(A) = P(R  A) + P(N  A)
=0.06+0.48=0.54

12. Extension of Example1
Consider P(R|A)
The conditional probability that it rains given
that sale is successful
the How do we calculate?
Using conditional probability formula
)
N
(
P
)
N
|
A
(
P
)
R
(
P
)
R
|
A
(
P
)
R
(
P
)
R
|
A
(
P
)
A
(
P
)
A
R
(
P
)
A
|
R
(
P







8
0
6
0
2
0
3
0
2
0
3
0
.
.
.
.
.
.




=
= 0.1111
*show slide 7

13. Example 2
 In a recent New York Times article, it was
reported that light trucks, which include
SUV’s, pick-up trucks and minivans,
accounted for 40% of all personal vehicles on
the road in 2002. Assume the rest are cars.
Of every 100,000 car accidents, 20 involve a
fatality; of every 100,000 light truck accidents,
25 involve a fatality. If a fatal accident is
chosen at random, what is the probability the
accident involved a light truck?

14. Example 2
Events
C- Cars
T –Light truck
F –Fatal Accident
N- Not a Fatal Accident
Given
P(F|C) = 20/10000 and P(F|T) = 25/100000
P(T) = 0.4
In addition we know C and T are complementary events
P(C)=1-P(T)=0.6
Our goal is to compute the conditional probability of a Light truck
accident given that it is fatal P(T|F).
)
T
C
( c


15. Goal P(T|F)
Consider P(T|F)
Conditional probability
of a Light truck accident
given that it is fatal
Using conditional
probability formula
)
F
(
P
)
F
T
(
P
)
F
|
T
(
P


S=CT
C T
F

16. P(T|F)-Method1
Consider P(T|F)
Conditional probability of a Light truck
accident given that it is fatal
How do we calculate?
Using conditional probability formula
)
C
(
P
)
C
|
F
(
P
)
T
(
P
)
T
|
F
(
P
)
T
(
P
)
T
|
F
(
P
)
F
(
P
)
F
T
(
P
)
F
|
T
(
P







)
.
)(
.
(
)
.
)(
.
(
)
.
)(
.
(
6
0
0002
0
4
0
00025
0
4
0
00025
0

=
= 0.4545

17. Tree Diagram- Method2
Vehicle
C
T
F C  F 0.6 0.0002 = .00012
F T  F 0.40.00025= 0.0001
N C  N 0.6 0.9998 = 0.59988
N T N 0.40.99975= .3999
0.6
0.4
0.9998
0.0002
0.00025
0.99975
Probability
Conditional
Probability
Probability
Event

18. Tree Diagram- Method2
)
F
C
(
P
)
F
T
(
P
)
F
T
(
P
)
F
(
P
)
F
T
(
P
)
F
|
T
(
P







)
.
)(
.
(
)
.
)(
.
(
)
.
)(
.
(
6
0
0002
0
4
0
00025
0
4
0
00025
0

=
= 0.4545

19. Partition
S
B1 B2 B3
A
)
(
)
|
(
)
(
)
|
(
)
(
)
|
(
)
( 3
3
2
2
1
1 B
P
B
A
P
B
P
B
A
P
B
P
B
A
P
A
P 






20. Law of Total Probability
))
(
)
(
)
((
))
(
(
)
(
)
(
2
1
2
1
n
n
B
A
B
A
B
A
P
B
B
B
A
P
S
A
P
A
P
















Let the events B1, B2, , Bn partition the finite discrete sample
space S for an experiment and let A be an event defined on S.

21. Law of Total Probability
























n
i
i
i
n
n
n
n
B
P
B
A
P
B
P
B
A
P
B
P
B
A
P
B
P
B
A
P
B
A
P
B
A
P
B
A
P
B
A
B
A
B
A
P
1
2
2
1
1
2
1
2
1
)
(
)
|
(
)
(
)
|
(
)
(
)
|
(
)
(
)
|
(
)
(
)
(
)
(
))
(
)
(
)
((



.
)
(
)
|
(
)
(
1




n
i
i
i B
P
B
A
P
A
P

22. Bayes’ Theorem
 Suppose that the events B1, B2, B3, . . . , Bn
partition the sample space S for some
experiment and that A is an event defined on
S. For any integer, k, such that
we have
n
k 

1
     
   


 n
j
j
j
k
k
k
B
P
B
A
P
B
P
B
A
P
A
B
P
1
|
|
|

23. Focus on the Project
Recall
 P(Y  T  C|S) will be used to calculate
P(S|Y  T  C)
 P(Y  T  C|F) will be used to calculate
P(F|Y  T  C)

24. How can Bayes’ Theorem help us with the
decision on whether or not to attempt a loan work
out?
Partitions
1. Event S
2. Event F
Given
P(Y  T  C|S)
P(Y  T  C|F)
Need
P(S|Y  T  C)
P(F|Y  T  C)

25. Using Bayes Theorem
P(S|Y  T  C)  0.477
 
)
536
.
0
(
)
021
.
0
(
)
464
.
0
(
)
022
.
0
(
)
464
.
0
(
)
022
.
0
(
)
(
)
|
(
)
(
)
|
(
)
(
)
|
(
|


















F
P
F
C
T
Y
P
S
P
S
C
T
Y
P
S
P
S
C
T
Y
P
C
T
Y
S
P
 
.
)
536
.
0
(
)
021
.
0
(
)
464
.
0
(
)
022
.
0
(
)
536
.
0
(
)
021
.
0
(
)
(
)
|
(
)
(
)
|
(
)
(
)
|
(
|


















F
P
F
C
T
Y
P
S
P
S
C
T
Y
P
F
P
F
C
T
Y
P
C
T
Y
F
P
LOAN FOCUS EXCEL-BAYES
P(F|Y  T  C)  0.523

26. RECALL
 Z is the random variable giving the amount of money,
in dollars, that Acadia Bank receives from a future
loan work out attempt to borrowers with the same
characteristics as Mr. Sanders, in normal times.
)
523
.
0
(
000
,
250
$
)
477
.
0
(
000
,
000
,
4
$
)
|
(
000
,
250
$
)
|
(
000
,
000
,
4
$
)
000
,
250
$
(
000
,
250
$
)
000
,
000
,
4
$
(
000
,
000
,
4
$
)
(


















C
T
Y
F
P
C
T
Y
S
P
Z
P
Z
P
Z
E
E(Z)  $2,040,000.

27. Decision
EXPECTED VALUE OF A WORKOUT=E(Z)  $2,040,000
FORECLOSURE VALUE- $2,100,000
RECALL
FORECLOSURE VALUE> EXPECTED VALUE OF A WORKOUT
DECISION
FORECLOSURE

28. Further Investigation I
 let Y  be the event that a borrower has 6, 7, or 8 years of
experience in the business.
Using the range
Let Z be the random variable giving the amount of
money, in dollars, that Acadia Bank receives from a
future loan work out attempt to borrowers with Y  and a
Bachelor’s Degree, in normal times. When all of the
calculations are redone, with Y  replacing Y, we find that P(Y 
 T  C|S)  0.073 and P(Y   T  C|F)  0.050.
Former Bank
Years In
Business
Years In
Business
Education
Level
State Of
Economy
Loan Paid
Back
BR >=6 <=8 yes

29. Calculations
P(Y   T  C|S)  0.073
P(Y   T  C|F)  0.050
P(S|Y   T  C)  0.558
P(F|Y   T  C)  0.442
The expected value of Z is E(Z )  $2,341,000.
Since this is above the foreclosure value of
$2,100,000, a loan work out attempt is
indicated.

30. Further Investigation II
 Let Y" be the event that a borrower has 5, 6,
7, 8, or 9 years of experience in the business
 Let Z" be the random variable giving the
amount of money, in dollars, that Acadia Bank
receives from a future loan work out attempt
to borrowers with 5, 6, 7, 8, or 9 years
experience and a Bachelor's Degree, in
normal times. Redoing our work yields the
follow results.

31. Similarly can calculate E(Z  )
 Make at a decision- Foreclose vs. Workout
 Data indicates Loan work out

32. Close call for Acadia Bank loan officers
Based upon all of our calculations, we
recommend that Acadia Bank enter into a
work out arrangement with Mr. Sanders.