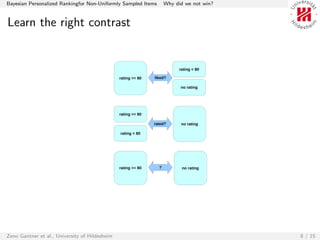
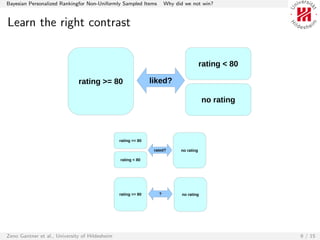
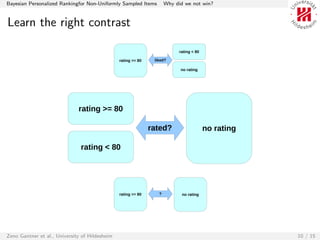
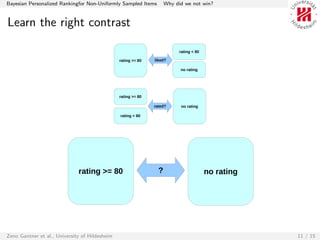
The document discusses Bayesian Personalized Ranking (BPR) for ranking items within the context of a competition. It explains the methodology adopted to tackle the item ranking problem using matrix factorization and introduces Weighted BPR to address issues with sampling bias in negative items. The authors reflect on the competition outcomes, acknowledging their model's effectiveness while also outlining areas for improvement and future exploration.

1. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items
Bayesian Personalized Ranking
for Non-Uniformly Sampled Items
Zeno Gantner, Lucas Drumond, Christoph Freudenthaler,
Lars Schmidt-Thieme
University of Hildesheim
21 August 2011
Zeno Gantner et al., University of Hildesheim 1 / 15

2. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Questions (and Answers)
What?
Who? Which?
How?
Where?
Why?
Zeno Gantner et al., University of Hildesheim 2 / 15

3. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Which problem to solve?
Which problem to solve?
Rating Prediction (Track 1)
vs.
Item Prediction (Track 2)
Zeno Gantner et al., University of Hildesheim 3 / 15

4. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items How did we tackle the problem?
How did we tackle the problem?
Bayesian Personalized Ranking:
2
BPR(DS ) = argmax ln σ(ˆu,i (Θ) − ˆu,j (Θ) )−λ Θ
s s
Θ
(u,i,j)∈DS
DS contains all pairs of positive and negative items for each user,
1
σ(x) = 1+e −x is the logistic function,
Θ represents the model parameters,
ˆu,i (Θ) is the predicted score for user u and item i, and
s
λ Θ 2 is a regularization term to prevent overfitting.
interpretation 1: reduce ranking to pairwise classif. [Balcan et al. 2008]
interpretation 2: optimize for smoothed area under the ROC curve (AUC)
Model: matrix factorization
Learning: stochastic gradient ascent
[Rendle et al., UAI 2009]
Zeno Gantner et al., University of Hildesheim 4 / 15

5. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items How did we tackle the problem?
How did we tackle the problem?
2
BPR(DS ) = argmax ln σ(ˆu,i − ˆu,j ) − λ Θ
s s
Θ
(u,i,j)∈DS
problem: all negative items j are given the same weight
Zeno Gantner et al., University of Hildesheim 5 / 15

6. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items How did we tackle the problem?
How did we tackle the problem?
2
BPR(DS ) = argmax ln σ(ˆu,i − ˆu,j ) − λ Θ
s s
Θ
(u,i,j)∈DS
problem: all negative items j are given the same weight
solution: adapt weights in the optimization criterion (and sampling
probabilities in the learning algorithm)
WBPR(DS ) = argmax wu wi wj ln σ(ˆu,i − ˆu,j ) − λ Θ 2 ,
s s
Θ
(u,i,j)∈DS
where
+
wj = δ(j ∈ Iu ). (1)
u∈U
Zeno Gantner et al., University of Hildesheim 5 / 15

7. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Why did we not win?
Why did we not win?
But also: Why did we perform better than others?
Why did we perform better than others?
straightforward model that matches the prediction task pretty well
scalability (e.g. k = 480 factors per user/item)
integration of rating information (see paper)
ensembles (see paper)
Why did we not win?
. . . two possible answers . . .
Zeno Gantner et al., University of Hildesheim 6 / 15

8. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Why did we not win?
Taxonomy
Zeno Gantner et al., University of Hildesheim 7 / 15

9. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Why did we not win?
Learn the right contrast
rating < 80
rating >= 80 liked?
no rating
rating >= 80
rated? no rating
rating < 80
rating >= 80 ? no rating
Zeno Gantner et al., University of Hildesheim 8 / 15

10. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Why did we not win?
Learn the right contrast
rating < 80
rating >= 80 liked?
no rating
rating >= 80
rated? no rating
rating < 80
rating >= 80 ? no rating
Zeno Gantner et al., University of Hildesheim 9 / 15

11. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Why did we not win?
Learn the right contrast
rating < 80
rating >= 80 liked?
no rating
rating >= 80
rated? no rating
rating < 80
rating >= 80 ? no rating
Zeno Gantner et al., University of Hildesheim 10 / 15

12. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Why did we not win?
Learn the right contrast
rating < 80
rating >= 80 liked?
no rating
rating >= 80
rated? no rating
rating < 80
rating >= 80 ? no rating
Zeno Gantner et al., University of Hildesheim 11 / 15

13. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Where?
Where next?
classification → ranking → pairwise classification
pairwise classification: try other losses, e.g. soft margin (hinge) loss
Bayesian2 Personalized Ranking
beyond KDD Cup: consider different sampling schemes . . .
Zeno Gantner et al., University of Hildesheim 12 / 15

14. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Summary
Summary
Use matrix factorization optimized for Bayesian
Personalized Ranking (BPR) to solve the item
ranking problem.
BPR reduces ranking (in this case: binary
variables) to pairwise classification.
Extend BPR to use different sampling scheme:
Weighted BPR (WBPR).
Open question: Learn a different contrast?
Details can be found in the paper.
Code: http://ismll.de/mymedialite/
examples/kddcup2011.html
advertisement: Contribute to http://recsyswiki.com!
Zeno Gantner et al., University of Hildesheim 13 / 15

15. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Questions
Zeno Gantner et al., University of Hildesheim 14 / 15

16. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items
Acknowledgements
Thank you
The organizers, for hosting a great competition.
The participants, for sharing their insights.
Funding
German Research Council (Deutsche Forschungsgemeinschaft, DFG) project
Multirelational Factorization Models.
Development of the MyMediaLite software was co-funded by the European
Commission FP7 project MyMedia under the grant agreement no. 215006.
Picture credits
by Michael Sauers, under Creative Commons by-nc-sa 2.0
http://www.flickr.com/photos/travelinlibrarian/223839049/
by Rob Starling, under Creative Commons by-sa 2.0
http://en.wikipedia.org/wiki/File:Air_New_Zealand_B747-400_ZK-SUI_at_LHR.jpg
Zeno Gantner et al., University of Hildesheim 15 / 15

17. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items
Numbers?
k error in %
“liked” contrast
320 5.52
480 5.08
“rated” contrast
320 5.15
480 4.87
Estimated error on validation split (not leaderboard).
Zeno Gantner et al., University of Hildesheim 16 / 15

18. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Advertisement
MyMediaLite: Recommender System Algorithm Library
functionality
rating prediction
item recommendation from implicit feedback
group recommendation
target groups simple
researchers, educators and students free
application developers scalable
development well-documented
written in C#, runs on Mono well-tested
GNU General Public License (GPL) choice
regular releases (ca. 1 per month)
http://ismll.de/mymedialite
Zeno Gantner et al., University of Hildesheim 17 / 15

19. Bayesian Personalized Rankingfor Non-Uniformly Sampled Items Advertisement
RecSys Wiki is looking for contributions
Alan
Zeno
http://recsyswiki.com
Zeno Gantner et al., University of Hildesheim 18 / 15