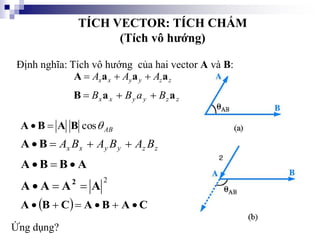
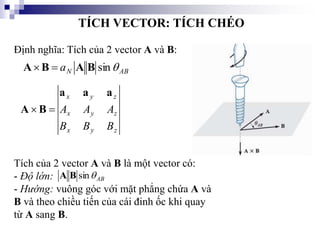
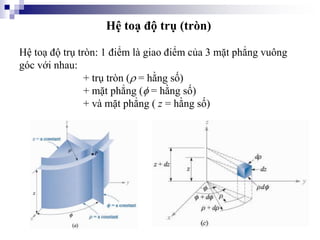
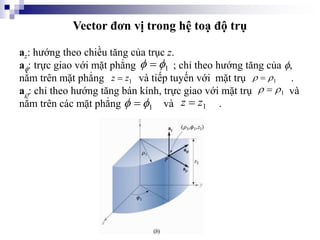
Tài liệu trình bày về kỹ thuật điện từ và phân tích vector trong môn kỹ thuật điện, giới thiệu các khái niệm về trường điện từ và cách xác định các vector trong không gian. Nó bao gồm các phép toán vector như cộng, trừ, tích chấm và tích chéo. Ngoài ra, tài liệu cũng đề cập đến các hệ tọa độ như tọa độ trụ và tọa độ cầu với các liên hệ giữa chúng.








![VÍ DỤ: Một trường vector S biểu diễn trong hệ toạ độ vuông góc là
S = {125/[(x-1)2 + (y-2)2 + (z+1)2 ]}{(x-1)ax + (y-2)ay + (z+1)az }.
a. Tính S tại P(2,4,3).
b. Xác định vector đơn vị theo hướng của S tại P.
c. Xác định bề mặt f(x, y, z) để 1
S](https://image.slidesharecdn.com/bai1phantichvector-230923085247-30fa5767/85/Bai-1-Phan-tich-vector-ppt-11-320.jpg)