青学時代の制御の輪読スライド。

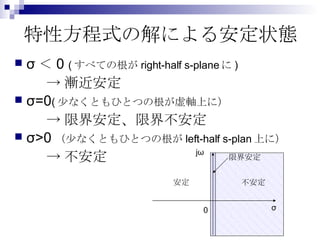
1. 輪講発表 第 7 回 6 月 18 日 教材： AUTOMATIC CONTROL SYSTEMS( 第 7 版 ) 著者 : BENJSMIN C. KUO 出版社 :PRENTICE HALL 担当範囲 : P327 ～ P360 担当者： 吉田新吾 学籍番号：15801078 出席番号：３H75

2. 今回の講義内容 BIBO (Bounded-Input Bounded-Output) Stability 特性方程式の解と安定性 零入力と漸近安定 Routh – Hurwitz 判定法

3. BIBO (Bounded-Input Bounded-Output) Stability 入力 u(t) 、 出力 y(t) 、インパルス g(t) として 時不変の線形システムを作ると zero I.C. において BIBO Stability となる。 畳み込み積分すると次のとおり

4. BIBO Stability(2) 今、両辺絶対値を取って |u(t)| が有限だとすると |y(t)| が有限となる。すると、 も有限といえる。 このことにより、インパルス応答を調べれば システムが安定かどうかを調べることができる

5. 特性方程式の解と安定性 G(s) を伝達関数とし、ラプラス変換して、 絶対値を取ると 次に とする。 σ はｓの実部。 s を G(s) のポールだとして G(s)=∞ とすると、

6. 特性方程式の解と安定性 (2) 特性方程式の解が right-half s-plane にあれば、 となる 先ほどの式は次のようになる。 このことは BIBO stability に反する -> BIBO stability において 特性方程式の解がシステムの安定性を決める

7. 零入力と漸近安定 数学的に次のような定義 今 y(t) についてだが、 x(t) についても 同様のことが言える 行列の場合は固有値について同じことが言える

8. 零入力と漸近安定(2) 2 次システムについて考えると 状態制御行列 φ(t) とすると よって ||X|| を求めると

9. 零入力と漸近安定(３) 定義より が安定の条件 よって

10. 特性方程式の解による安定状態 σ＜0 ( すべての根が right-half s-plane に ) ->漸近安定 σ=0 ( 少なくともひとつの根が虚軸上に） ->限界安定、限界不安定 σ>0 （少なくともひとつの根が left-half s-plan 上に） ->不安定 0 σ jω 限界安定 安定 不安定

11. 安定を決める方法 システムをデザインするときに、 変数をどのように埋め込めばいいかを 調べる方法。代表的なものに以下の３つ Routh – Hurwitz の判定法 Nyquist の判定法 ボード線図 ここではRouth – Hurwitzの判定法を扱う

12. Routh - Hurwitz判定法 特性方程式を F(s) とすると、 ( 全ての係数は実数） この式が正の実数の根を持たないためには （安定するには）次の条件が必要 全ての係数は同じサインを持つ 係数が消えてはならない

13. Hurwitz判定法 Routh - Hurwitz判定法のもと Hurwitzの行列式が全て正なら 安定。Hurwitzの行列式は次のとおり

14. Routh - Hurwitz判定法(2) Routh 表は次のとおり 初めの列でサインが変わらなければ安定 同様にサインが何回変わったかを数えれる

15. Routh - Hurwitz判定法 例 次の特性方程式について考える Sign change Sign change Sign Change は 2 回起こっている。実際に解を求めると s=-1.0055±j0.933311 と s=0.7555±j1.4444 である

16. Special Case 1 初めの列に0が出てきて、 他の要素は0でない場合 0となるところを任意の小さな正の数εを 置きその後を計算する。

17. Special Case 1 例題 次の特性方程式について考える sign change が 2 回起こっていることがわかる Sign change Sign change

18. Special Case 2 : zero row 全ての行の要素が 0 となる場合次のような検討をする ひとつ上の行を補助方程式 A(s)=0 としてとる A(s) を s について微分する その係数を zero row の係数としておき判定を続ける zero row が起こると補助方程式の解が 原点に対し対象となる -> 安定性の判定は補助方程式の解を解いて決める

19. Special Case 2 例題 次の特性方程式について考える 補助方程式を次のようにする zero row

20. Special Case 2 例題 続き A(s) を微分する テーブルは次のようになる 安定しているように見えるが 実際に A(s) の解を求めると、 s=±j となる。 -> 限界安定