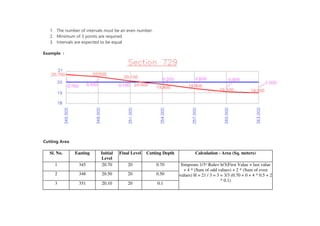
Simpson's 1/3 rule is a numerical integration method that divides the area under a curve into strips. It assumes the curve within each strip is parabolic rather than linear. The area is calculated by adding the areas of each strip, weighing the middle terms by 4 and outside terms by 1. It requires an even number of intervals with a minimum of 3 points, and equal spacing between intervals. An example shows how to apply the rule to calculate cut and fill areas from elevation data by summing the weighted height values within each interval.

1. Area Calculation - Simpsons One Third Rule
Simpson’s 1/3rd rule is one of the most popular methods of finding the area for a given set of points by the method of numerical
integration. The basic idea is to divide the X-axis into equally spaced divisions as shown and to complete the top of these strips
of an area in such a way that we can calculate the area by adding up these strips
Simpson's rule is based on a parabolic model of the function to be integrated (that is instead of connecting 2 adjacent points
merely by a straight line, a parabola is chosen such that the curve formed by joining these points is extremely smooth and thus
helps in calculating the area).
Where the sum of odd and even terms do not include the first and the last terms
Important points to be considered while applying Simpson’s Rule are:

2. 1. The number of intervals must be an even number.
2. Minimum of 3 points are required
3. Intervals are expected to be equal
Example :
Cutting Area
Sl. No. Easting Initial
Level
Final Level Cutting Depth Calculation - Area (Sq. meters)
1 345 20.70 20 0.70 Simpsons 1/3rd
Rule= h/3(First Value + last value
+ 4 * (Sum of odd values) + 2 * (Sum of even
values) H = 21 / 3 = 3 = 3/3 (0.70 + 0 + 4 * 0.5 + 2
* 0.1)
2 348 20.50 20 0.50
3 351 20.10 20 0.1

3. 4 354 19.80 20 0
5 357 19.40 20 0
6 360 19.10 20 0
7 363 19.00 20 0
Total = 2.9
Filling Area
Sl. No. Easting Initial
Level
Final Level Cutting Depth Calculation - Area (Sq. meters)
1 345 20.70 20 0 Simpsons 1/3rd
Rule= h/3(First Value + last value
+ 4 * (Sum of odd values) + 2 * (Sum of even
values)
H = 21 / 3 = 3
= 3/3 (0 + 1.00 + 4 * 1.1 + 2 * 0.4)
2 348 20.50 20 0
3 351 20.10 20 0
4 354 19.80 20 0.20
5 357 19.40 20 0.60
6 360 19.10 20 0.90
7 363 19.00 20 1.00
Total = 6.6