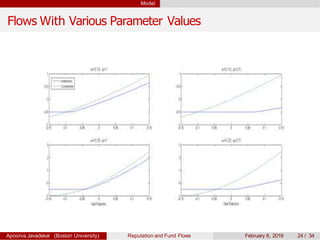
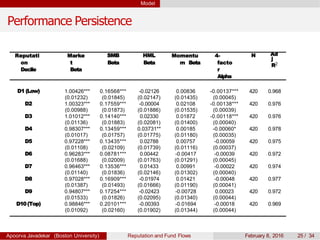
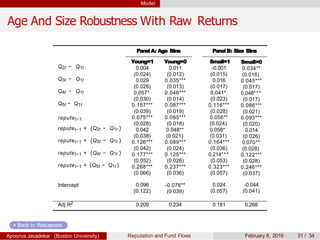
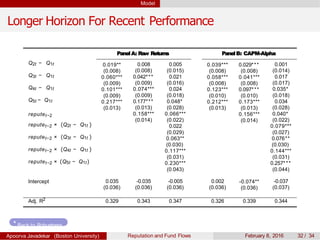
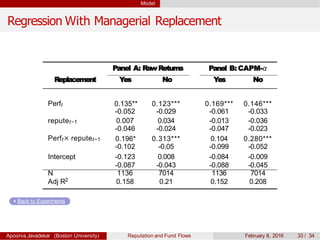
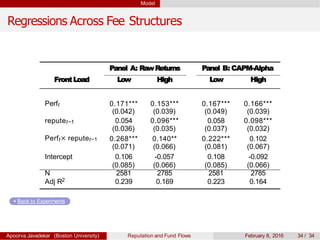
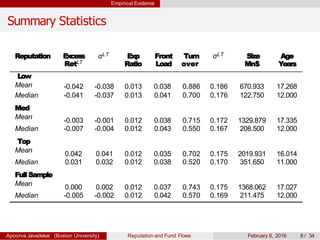
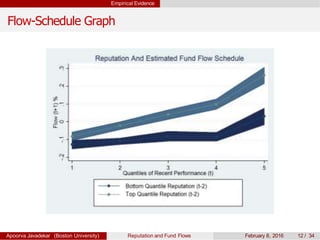
The paper explores the influence of mutual fund reputation on fund flows, highlighting that reputation affects how past performance impacts future fund flows. It discusses how investor behavior and managerial incentives relate to fund performance and reputation, using empirical data to demonstrate significant interactions between reputation and return outcomes. The findings indicate that higher-reputed funds experience more significant performance-driven inflows compared to lower-reputed counterparts.






![Empirical Evidence
Variables
Fund Flows:
FLOWit =
qit − [qit−1 × (1 + rit )]
it−1 × itq (1 + r )
where rit denotes net of expense fund returns during time t and qit
denotes fund assets at the end of time t.
Fund Performance:
Rankswithin same’investmentobjective’ basedon raw net returns
(Sirri & Tuffano; 1998)
Ranks based upon ’CAPM-Alpha’ (Berk & Binsbergen; 2014)
Ranks are normalized to lie between [0, 1]interval.
Current Performance (Perfit ): Based upon current year t
Reputation(reputeit): Basedupon 5yearwindow ending with
current yeart.
Apoorva Javadekar (Boston University) Reputation and Fund Flows February 8, 2016 7 / 34](https://image.slidesharecdn.com/reputationflowsapoorvajavadekarnov2015-160216072405/85/Apoorva-JavdekarHow-Does-Mutual-Fund-Reputation-Affect-Subsequent-Fund-Flows-7-320.jpg)










![Model
Solution With δ < 1
Initial Investor Composition: A investor’s ownership at t = 0 is
λ0 =
µ
µ + (1 − µ)δ
s
F
¸¸
EcAttentive raction In
x
onomy
Competitive Size and Flows: qt
∗satisfy
tEt [rt+1|ht,q∗] = 0
andrequired flows
e∗ ∗
t = qt − qt−1(1 + rt )
Attentive Capital:
zt = λt −1 t−1+ (1 − λ )δ
A
s
ttentive Fraction
¸¸
Within
x
Fund
t −1 tq (1 + r )
Apoorva Javadekar (Boston University) Reputation and Fund Flows February 8, 2016 20 / 34](https://image.slidesharecdn.com/reputationflowsapoorvajavadekarnov2015-160216072405/85/Apoorva-JavdekarHow-Does-Mutual-Fund-Reputation-Affect-Subsequent-Fund-Flows-20-320.jpg)