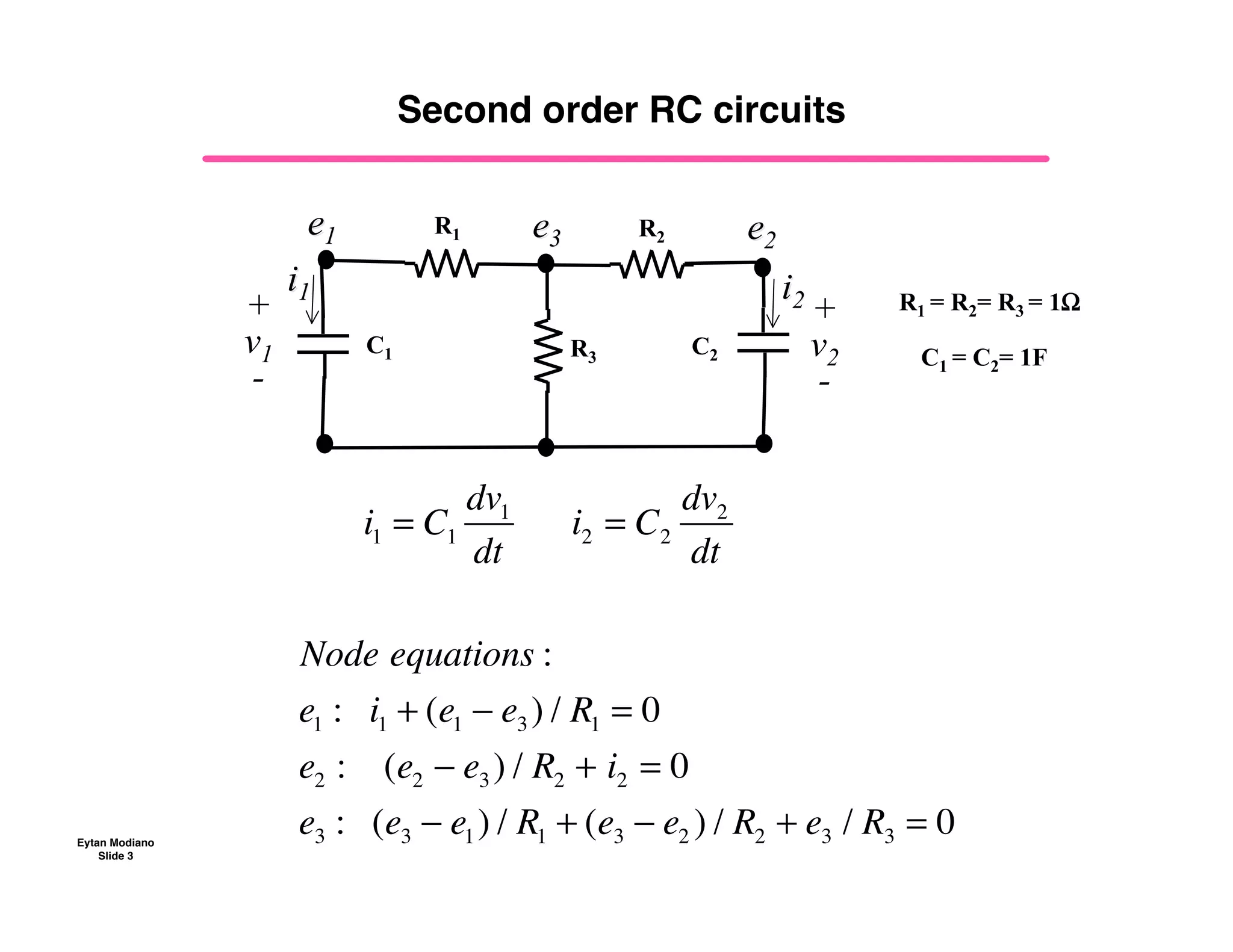
1) The document analyzes RC circuits using differential equations to model the voltage over time across capacitors with no input. 2) It derives the differential equations for a circuit with two capacitors and resistors, which form a system of homogeneous differential equations. 3) The document solves the system by guessing an exponential solution, finding the characteristic equation to get the exponents, and obtaining the general solution as a linear combination of specific solutions with coefficients determined by initial conditions.

1. Eytan Modiano
Slide 1
Analysis of RC circuits
Eytan Modiano

2. Eytan Modiano
Slide 2
Learning Objectives
• Analysis of basic circuit with capacitors, no inputs
– Derive the differential equations for the voltage across the capacitors
• Solve a system of first order homogeneous differential equations
using classical method
– Identify the exponential solution
– Obtain the characteristic equation of the system
– Obtain the natural response of the circuit
– Solve for the complete solution using initial conditions

3. Eytan Modiano
Slide 3
Second order RC circuits
i
i2
2 +
v2
-
i
i1
1
+
v1
-
R1 R2
R3
C1 C2
e
e1
1 e
e2
2
e
e3
3
R1 = R2= R3 = 1Ω
C1 = C2= 1F
!!!!!!!i1 = C1
dv1
dt
!!!!!!i2 = C2
dv2
dt
Node equations :
e1 :!!!i1 + (e1 ! e3 ) / R1 = 0
e2 :!!!!(e2 ! e3 ) / R2 +!i2 = 0
e3 :!!!(e3 ! e1) / R1 + (e3 ! e2 ) / R2 + e3 / R3 = 0

4. Eytan Modiano
Slide 4
The differential equations
!!!!!!!!!!!!!!!!Note :!!!v1!= e1 !;v2!= e2
Differential equations:
C1
de1
dt
+ (e1 ! e3 ) / R1 = 0
C2
de2
dt
+ (e2 ! e3 ) / R2 = 0
(e3 ! e1) / R1 + (e3 ! e2 ) / R2 + e3 / R3 = 0
Plugging!in!values! for!resistors!capacitors :
(1) !
e1 + e1 ! e3 = 0
(2) !
e2 + e2 ! e3 = 0
(3)!3e3 ! e2 ! e1 = 0

5. Eytan Modiano
Slide 5
Guessing a solution
Guess!ei = Eiest
!! !
ei = Eisest
E1sest
+ E1est
! E3est
= 0
E2sest
+ E2est
! E3est
= 0
3E3est
! E2est
! E1est
= 0
"
#
$
%
$
&
E1s + E1 ! E3 = 0
E2s + E2 ! E3 = 0
3E3 ! E2 ! E1 = 0
E1(1+ s) !! ! E3 = 0
E2 (1+ s) ! E3 = 0
!E1 !!!!!!!E2 !!!!!!!!!!!+3E3 = 0
We “guess” that the solution is an exponential of the
form:

6. Eytan Modiano
Slide 6
Solution to homogeneous equations
• If equations are linearly independent we have one unique solution:
– E1=E2=E3=0
– “trivial” solution
• In order to obtain non-trivial solution, the equations cannot be linearly
independent
– For what values of s are the equations not linearly independent?
• Rewrite equations in the form: AE = 0
• Rows of A are linearly dependent if determinant of A = 0
– Non-trivial solution
(1+ s) 0 !1
0 1+ s !1
!1 !1 3
"
#
$
$
$
%
&
'
'
'
E1
E2
E3
"
#
$
$
$
%
&
'
'
'
= 0

7. Eytan Modiano
Slide 7
The characteristic equation
det A = 0 (The characteristic equation)
see!linear!algebra!primer!on taking!determinants
A = 3(1+ s)(1+ s) ! (1+ s) ! (1+ s) = 0
3s2
+ 4s +1 = 0 " s =
!4 ± 16 !12
6
=
!4 ± 2
6
" s1 = !1,!s2 = !1/ 3
Two!solutions :
s = !1" ei = Eie!t
s = !1/ 3 " ei = Eie!t /3

8. Eytan Modiano
Slide 8
Non-trivial solution
• Now we must solve for the values of Ei’s
• Recall
• For s = -1 we have,
E1(1+ s) !! ! E3 = 0
E2 (1+ s) ! E3 = 0
!E1 !!!!!!!E2 !!!!!!!!!!!+3E3 = 0
E1(0) !! ! E3 = 0 " E3 = 0
E2 (0) ! E3 = 0 " E3 = 0
!E1 !!!!!!!E2 !!!!!!!!!!!+3E3 = 0 " E1 =!!E2 !
Solution!not!unique,!choose :!!E2 = 1,!E1 = !1
" e1 = !1e!t
,!!e2 = 1e!t
,!e3 = 0

9. Eytan Modiano
Slide 9
Non-trivial solution, continued
• Similarly, for s = -1/3
• Note that in general we can solve for the E’s using row reduction, etc. (see
linear algebra notes)
E1(2 / 3) !! ! E3 = 0 " E1 = 3 / 2E3
!!E2 (2 / 3) ! E3 = 0 " E2 = 3 / 2E3
!E1 !!!!!!!E2 !!!!!!!!!!!+3E3 = 0
Solution!not!unique,!choose :!!E3 = 1,!E1 = E2 = 3 / 2
" e1 = 3 / 2e!t /3
,!!e2 = 3 / 2e!t /3
,!e3 = e!t /3

10. Eytan Modiano
Slide 10
The complete solution
• We now have two possible solutions:
• Since the system is linear and homogeneous, any linear combination of
these solution is also a solution. Hence,
• Where a, and b are constants that depend on initial conditions
– Given initial values for e1 = v1 and e2 = v2 we can solve for a and b
(1) :!!!e1 = 3 / 2e!t /3
,!!e2 = 3 / 2e!t /3
,!e3 = e!t /3
(2) :!!e1 = !1e!t
,!!e2 = 1e!t
,!e3 = 0
!
e(t) = a
!1
1
0
"
#
$
$
$
%
&
'
'
'
e!t
+ b
3 / 2
3 / 2
1
"
#
$
$
$
%
&
'
'
'
e!t /3

11. Eytan Modiano
Slide 11
The complete solution, continued
• Suppose we are given the initial voltage values across the
capacitors: e1(0) = v1(0), e2(0) = v2(0)
• Plug these into the solution
to obtain:
! a =
e2 (0) " e1(0)
2
,!!b =
e1(0) + e2 (0)
3
Finally,
e1(t) =
e1(0) " e2 (0)
2
e"t
+
e1(0) + e2 (0)
2
e"t /3
e2 (t) =
e2 (0) " e1(0)
2
e"t
+
e1(0) + e2 (0)
2
e"t /3
e3(t) =
e1(0) + e2 (0)
3
e"t /3
e1(0) = !ae0
+ 3 / 2be0
= !a + 3 / 2b
e2 (0) = ae0
+ 3 / 2be0
=!!a + 3 / 2b
"
#
$
%
$
&