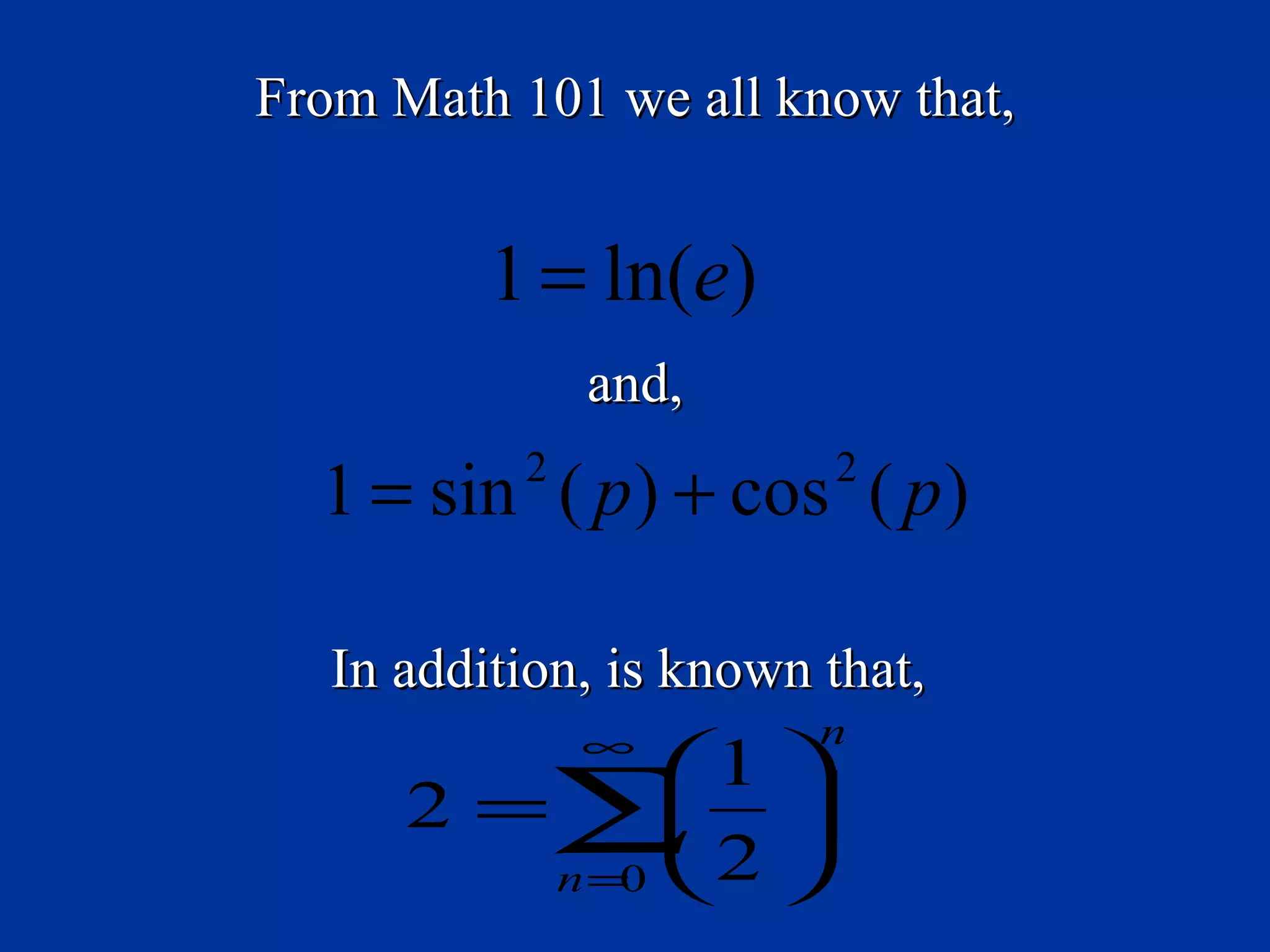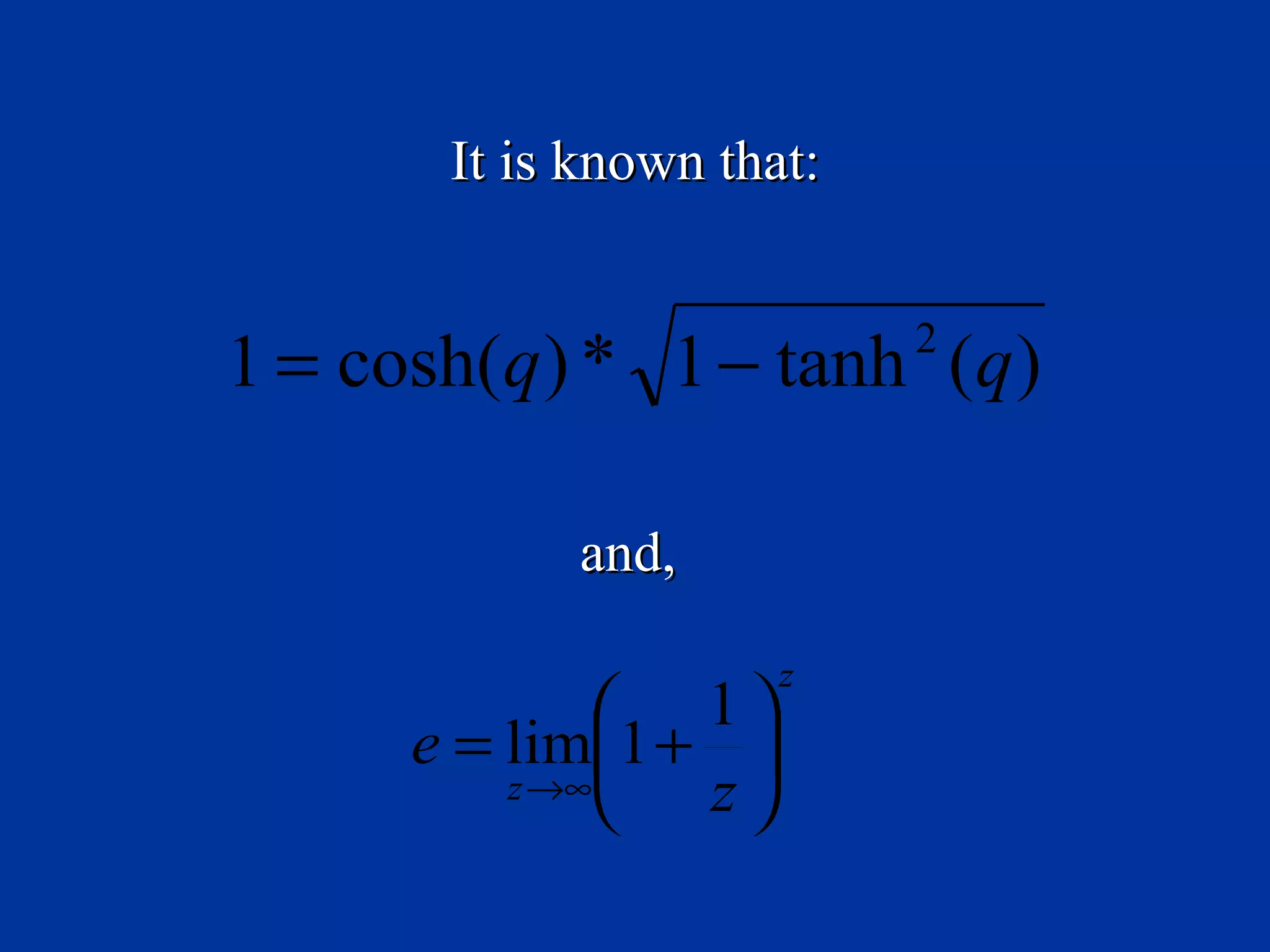The document discusses rewriting a simple mathematical equation, 1+1=2, in a more "elegant" and "comprehensive" manner using advanced mathematical notation and terms. It proceeds to transform the simple equation through multiple steps incorporating logarithmic, exponential, trigonometric and other advanced functions. The resulting equation is much longer and more complex, though purportedly more "professional". The presentation is intended in jest to show that engineers can also overcomplicate simple concepts.

1. Professional Elegance...
Any engineer learn the mathematical notation in
which the addition of two real numbers, say,
1+1 = 2
can be written in a very simple form.
But, we can say that it lacks totally from style.

2. From Math 101 we all know that,
1 = ln(e)
and,
1 = sin ( p ) + cos ( p )
2 2
In addition, is known that,
∞ n
1 
2 =∑  
n=  2 
0

3. Therefore the expression,
1+1 = 2
Can be re-written in a more elegant way such as,
∞ n
1
ln ( e ) + sin ( p ) + cos ( p ) = ∑  
2 2
n =0  2 
which as we can see, it is more comprehensive and
scientific.

4. It is known that:
1 = cosh(q ) * 1 − tanh (q )
2
and,
z
 1
e = lim1 + 
z →∞
 z

5. that results in,
∞ n
1
ln ( e ) + sin ( p ) + cos ( p ) = ∑  
2 2
n =0  2 
Which can be written in a clear and transparent way
as,
  1 2  ∞
cosh(q ) * 1 − tanh 2 (q)
ln lim1 +   + sin 2 ( p ) + cos 2 ( p ) = ∑
 z →∞ z  2n
  n =0

6. Taking in account that,
0!= 1
And that the inverse matrix of the transposed matrix is
equal to the transposed matrix of the inverse matrix
(with the hypothesis of an onedimensional space), we
find the following simplified expression (using
vectorial notation),
(X ) − (X )
T −1 −1 T
=0

7. If we unify the simplified expressions,
0!= 1
and,
(X ) − (X )
T −1 −1 T
=0
It is obvious to obtain,

( ) − (X )
 X

T −1 −1 T 
!= 1


8. Applying the described simplifications, we can see
that from the equation:
  1 2  ∞
cosh(q ) * 1 − tanh 2 (q )
ln lim1 +   + sin ( p ) + cos ( p ) = ∑
2 2
 z →∞ z   2n
  n =0
we finally obtain in an totally elegant, legible,
succinct, and comprehensive form, the equation:
  T
( ) − (X ) 
2
−1 −1 T  1  + sin 2 ( p ) + cos 2 ( p ) = ∑
∞
cosh(q ) * 1 − tanh 2 (q )
ln lim  X !+ 
 z →∞   z  2n
  n =0
which it is much more professional than the vulgar, and
plebeian initial equation:
1 +1 = 2

9. This presentation has been designed specially for our dear
friends……the Lawyers; to let them know that Engineers can
make simple things real complicated as well!
And, of course…….., it is dedicated to our colleagues… the
Engineers, for them to feed the “little inside animal” called
EGO.
Enjoy it !!