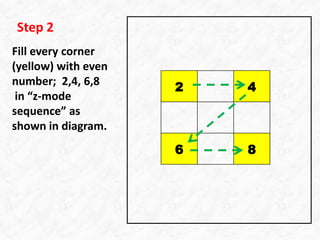
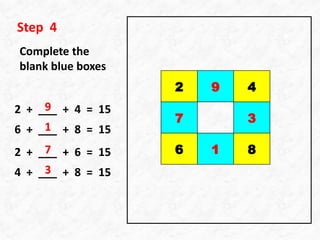
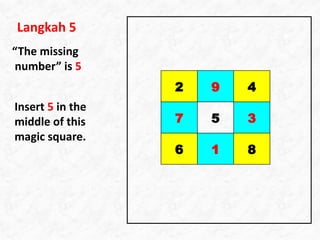
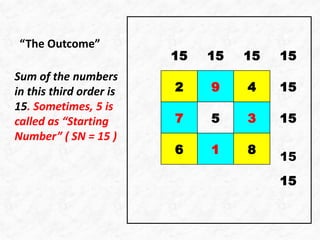
This document outlines 5 steps to construct a 3x3 magic square using integers 1 to 9 where the sum of each row, column and diagonal is 15. It involves first filling the corners with even numbers in a z-pattern, then calculating the missing values using the sum condition. The missing number, 5, is then placed in the center to complete the magic square.

1. An alternative method
to construct
“Magic Square 3x3”
Conditions:
1. We are going to complete this magic
square with integers 1 to 9.
2. The Sum of the Numbers is 15 (SN=15)
3. We are not tend to find out Desired
Number (DN).

2. Step 1
Construct blank
magic square 3x3.
(Third Order)

3. Step 2
Fill every corner
(yellow) with even
number; 2,4, 6,8
in “z-mode
sequence” as
shown in diagram.
2
4
6
8

4. Step 3
Fill the blank blue
boxes with this
calculation.
2
4
6
8
2 + ___ + 4 = 15
6 + ___ + 8 = 15
2 + ___ + 6 = 15
4 + ___ + 8 = 15
Remember:
The Sum of the
numbers is 15

5. Step 4
Complete the
blank blue boxes
2
9
2 + ___ + 4 = 15
1
6 + ___ + 8 = 15
7
2 + ___ + 6 = 15
3
4 + ___ + 8 = 15
9
7
6
4
3
1
8

6. Step 5
“The missing
number” is 5
2
Insert 5 in the
middle of this
magic square.
9
4
7
5
3
6
1
8

7. “The Outcome”
Sum of the numbers
in this third order is
15. Sometimes, 15
is called as
“Starting Number” (
SN = 15 )
15
15
15
15
2
9
4
15
7
5
3
15
6
1
8
15
15

8. Thanks for viewing…