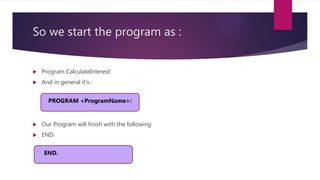
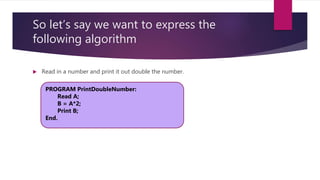
The document discusses algorithms and pseudocode, explaining the phases of programming: problem solving and implementation. It emphasizes the role of pseudocode in designing algorithms using an informal language similar to English, and provides various examples of algorithms for tasks such as calculating interest, checking odd/even numbers, and identifying prime numbers. The text also includes practical programming tasks, such as reversing integers and strings, checking for palindromes, capitalizing sentences, and counting vowels.

1. Algorithms & Pseudocode
BY M. QURESHI

2.  A typical programming task can be divided into two phases:
 Problem solving phase
 produce an ordered sequence of steps that describe solution of problem
 this sequence of steps is called an algorithm
 Implementation phase
 implement the program in some programming language

3. Steps in problem Solving
 Produce a general Algorithm
 Refine the algorithm Successively to get step by step detailed algorithm
that is very close to a computer language.
 Pseudocode is an artificial and informal language that helps programmers
develop algorithms Pseudocode is very similar to everyday English

4. Pseudocode
 The first thing we do when designing a program is to decide
on a name for the program
 Let’s say we want to write a program to calculate interest, a
good name for the program would be CalculateInterest.
 Note the use of CamelCase.

5.  Pseudocode is used to represent the logic of the solution to a problem.
 Once the pseudocode is verified, it can be converted into a program using the
vocabulary and syntax of a programming language
 Keywords in Pseudocode.
 Begin … End: these keywords are used to start and finish pseudocode. Begin is
the first line and end is the last line of pseudocode.
 Accept: This keyword is used to obtain an input from a user.
 Display: this keyword is used to present a result or an output.
 If .. Else .. End if : These keywords are used in decision-making.
 //: Comment
 Do .. While, for … repeat … until : Represent loop

6. So we start the program as :
 Program CalculateInterest:
 And in general it’s :
 Our Program will finish with the following
 END.
PROGRAM <ProgramName>:
END.

7. So let’s say we want to express the
following algorithm
 Read in a number and print it out double the number.
PROGRAM PrintDoubleNumber:
Read A;
B = A*2;
Print B;
End.

8. So let’s say we want to express the
following algorithm
 Read in a number, check if it is odd or even.
PROGRAM IsOddOrEven:
Read A;
If (A/2 gives a remainder)
Then Print “Its’s Odd”;
Else Print ”It’s Even”;
EndIf;
End.

9. So let’s say we want to express the following
algorithm to print out the bigger of two
numbers:
 Read in two numbers, call them A and B. Is A is bigger than B, print out A,
otherwise print out B.
PROGRAM PrintBiggerOfTwo:
Read A;
Read B;
If (A>B)
Then Print A;
Else Print B;
EndIf;
End.

10. So let’s say we want to express the following
algorithm to print out the bigger of three
numbers:
 Read in three numbers, call them A, B and C.
 If A is bigger than B, then if A is bigger than C, print out A, otherwise print out C.
 If B is bigger than A, then if B is bigger than C, print out B, otherwise print out C.

11. PROGRAM BiggerOfThree:
Read A;
Read B;
Read C;
If (A>B)
then If (A>C)
Then Print A;
Else Print B;
End If;(B>C)
Then Print B;
Else Print C;
End If;
End If;
End.

12. So let’s say we want to express the
following algorithm:
 Print out the numbers from 1 to 5
PROGRAM Print1to5:
A=1;
WHILE ( A !=6)
Do Print A;
A= A+1;
ENDWHILE;
End.

13. So let’s say we want to express the
following algorithm:
 – Add up the numbers 1 to 5 and print out the result
PROGRAM PrintSum1to5:
Total =0;
A=1;
WHILE ( A !=6)
Do Total = total +A;
A= A+1;
ENDWHILE;
Print Total;
End.

14. So let’s say we want to express the
following algorithm:
 – Read in a number and check if it’s a prime number.
 What’s a prime number?
 – A number that’s only divisible by itself and 1, e.g. 7.
 Or to put it another way, every number other than itself and 1 gives a remainder,
e.g. For 7, if 6, 5, 4, 3, and 2 give a remainder then 7 is prime.
 – So all we need to do is divide 7 by all numbers less than it but greater than one,
and if any of them have no remainder, we know it’s not prime.

15.  So,
 If the number is 7, as long as 6, 5, 4, 3, and 2 give a remainder, 7 is prime.
 If the number is 9, we know that 8, 7, 6, 5, and 4, all give remainders, but 3 does
not give a remainder, it goes evenly into 9 so we can say 9 is not prime.
 So remember, – if the number is 7, as long as 6, 5, 4, 3, and 2 give a remainder,
prime.
 So, in general, – if the number is A, as long as A-1, A-2, A-3, A4, ... 2 give a
remainder, A is prime.

16. PROGRAM prime:
Read A;
B = A-1;
IsPrime = True;
While(B !=1)
DO IF ( A/B gives no remainder)
THEN IsPrime = false;
End If
B=B-1;
ENDWHILE;
If(IsPrime ==true)
Then Print “Prime”;
Else Print “Not Prime”;
EndIf;
End.

17. Write Algorithm & Pseudocode & then
Actual Code
Write a Program to Reverse an Integer
// --- Directions
// Given an integer, return an integer that is the reverse
// ordering of numbers.
// --- Examples
// reverseInt(15) === 51
// reverseInt(981) === 189
// reverseInt(500) === 5
// reverseInt(-15) === -51
// reverseInt(-90) === -9

18. Write a Program to Reverse a String
// --- Directions
// Given a string, return a new string with the reversed
// order of characters
// --- Examples
// reverse('apple') === 'leppa'
// reverse('hello') === 'olleh'
// reverse('Greetings!') === '!sgniteerG'

19. Write a program to Find Palindromes
 // --- Directions
 // Given a string, return true if the string is a palindrome
 // or false if it is not. Palindromes are strings that
 // form the same word if it is reversed. *Do* include spaces
 // and punctuation in determining if the string is a palindrome.
 // --- Examples:
 // palindrome("abba") === true
 // palindrome("abcdefg") === false

20. Write a Program that will capitalize a
sentence
 // --- Directions
 // Write a function that accepts a string. The function should
 // capitalize the first letter of each word in the string then
 // return the capitalized string.
 // --- Examples
 // capitalize('a short sentence') --> 'A Short Sentence'
 // capitalize('a lazy fox') --> 'A Lazy Fox'
 // capitalize('look, it is working!') --> 'Look, It Is Working!'

21. Write a function that returns the number
of vowels
 // --- Directions
 // Write a function that returns the number of vowels
 // used in a string. Vowels are the characters 'a', 'e'
 // 'i', 'o', and 'u'.
 // --- Examples
 // vowels('Hi There!') --> 3
 // vowels('Why do you ask?') --> 4
 // vowels('Why?') --> 0