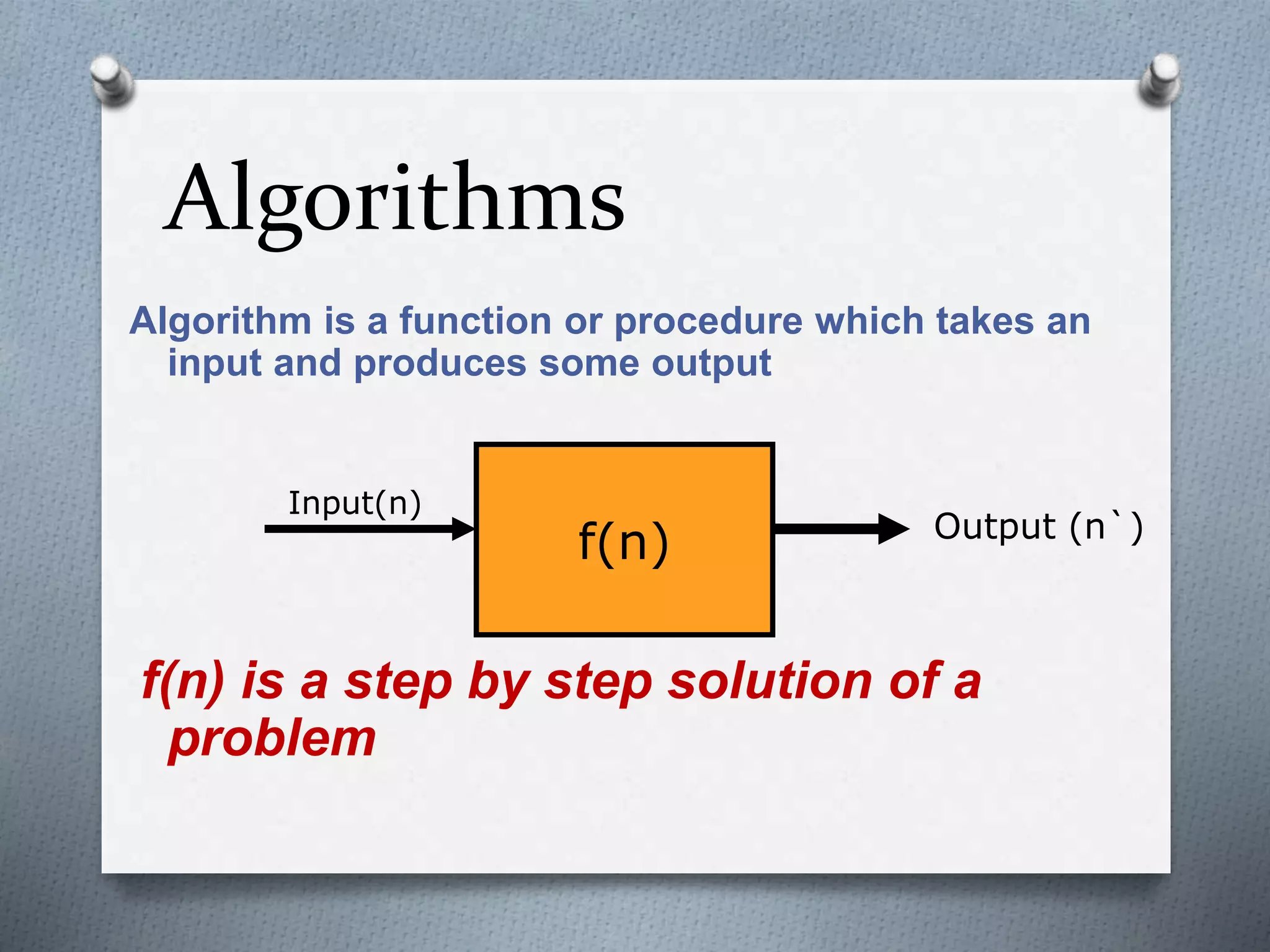
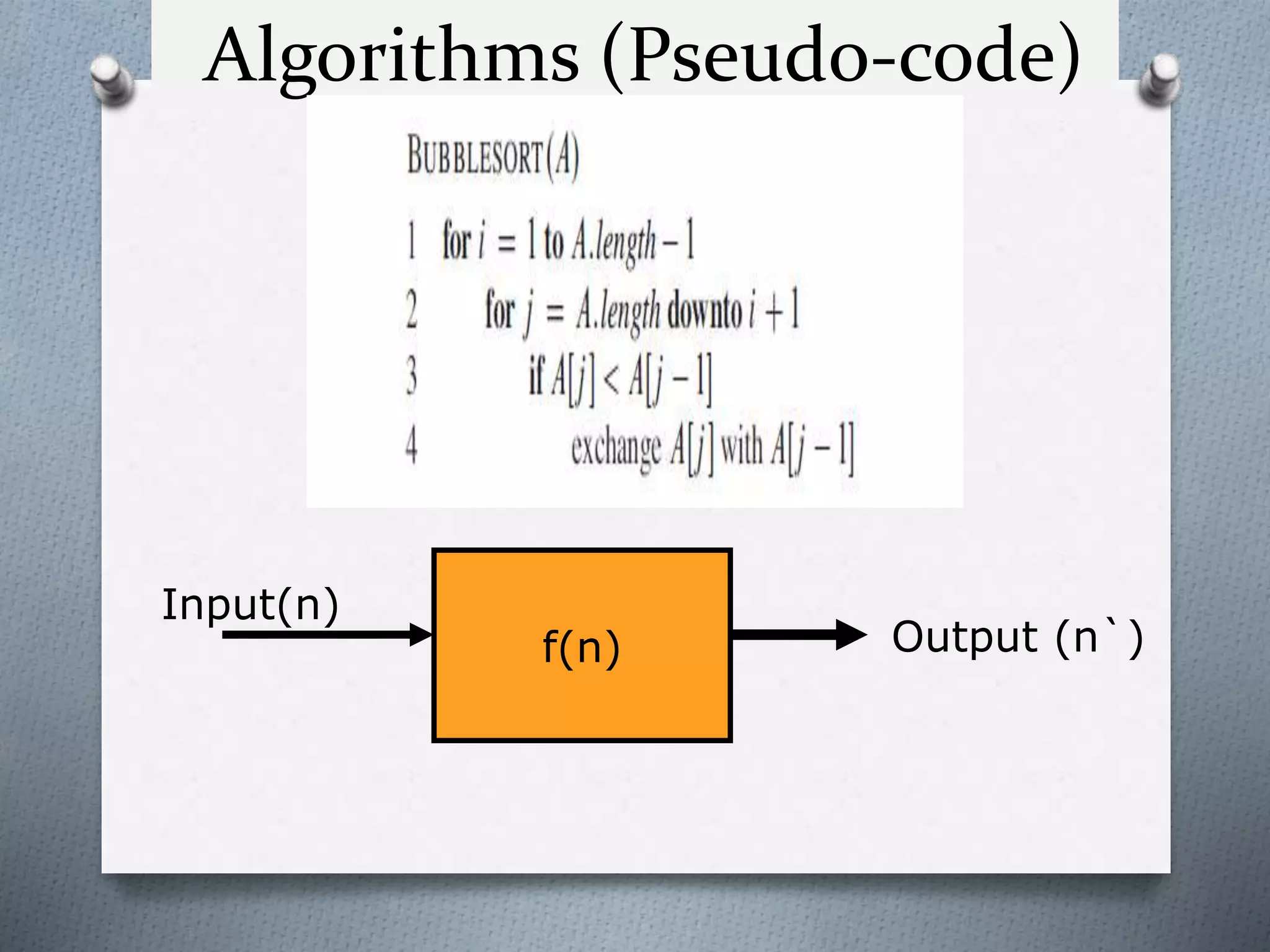
The document summarizes an algorithm lecture that covered the following topics: 1. The definition of an algorithm as a well-defined computational function or procedure that takes input and produces output. Pseudo-code and flowcharts are common styles for writing algorithms. 2. The history of algorithms, which originated with the mathematician al-Khowarizmi in the 9th century. 3. An introduction to the course syllabus, which will cover sorting algorithms, advanced design techniques like dynamic programming and greedy algorithms, and graph algorithms and NP-complete problems. 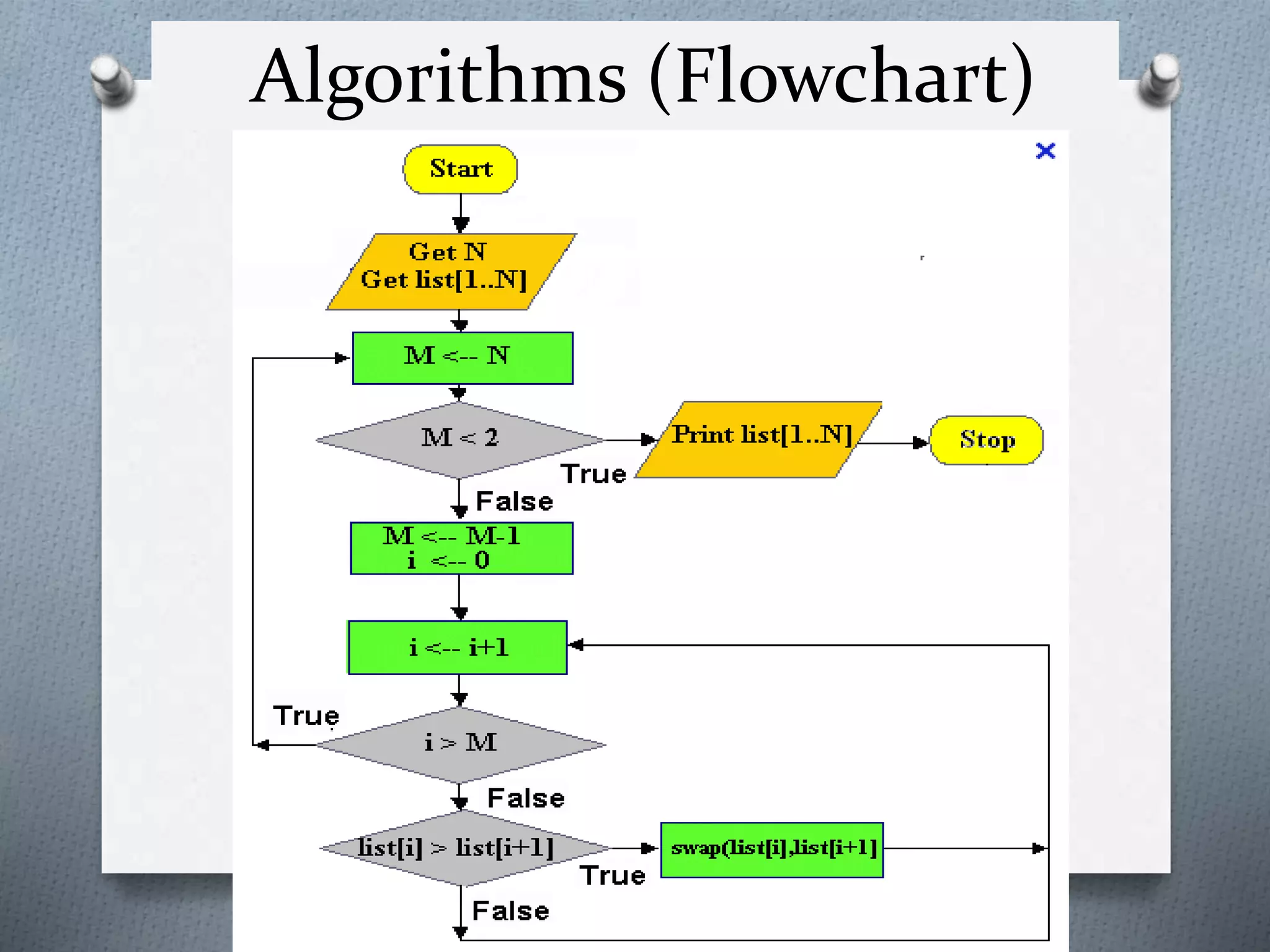4. A selection problem example is used to demonstrate algorithm design and analysis procedures. The goal is to select the fastest laptops that are not

1. Lecture # 1-3

2. Today’s Agenda
ODefinition
OAlgorithm Writing Styles
OHistory
OIntroduction to the syllabus

3. Algorithm?

4. Definition of Algorithm
OAny computing problem can be
solved by executing a series of
actions in a specific order, that is
called algorithm
OAlgorithm is a well-defined
computational function or
procedure that take some value or
set of values as an input and
produces some value or set of
value as an output

5. Algorithms
Algorithm is a function or procedure which takes an
input and produces some output
f(n) is a step by step solution of a
problem
f(n)
Input(n)
Output (n`)

6. Algorithm Writing Style..
OAlgorithm can be written in any manner
unless they provide the solution of a
problem (Correct )
OWhy to write Algorithm?
OTwo styles are mostly commonly used:
OPseudo-code
OFlow Chart

7. Algorithms (Pseudo-code)

8. Algorithms (Flowchart)

9. Ovoid bubbleSort(int Size, number[]){
Ofor(int i=0;i<Size-1;i++){
O for(int j=0;j<Size-1;j++){
Oif(number[j]<number[j+1]){
O int temp=number[j];
O number[j]=number[j+1];
O number[j+1]=temp;
O }
O }
O}
Algorithms (c++ Code)

10. What is Preferable….
Pseudo-code

11. Algorithms (Pseudo-code)
Pseudo-code conventions in page
20 & 21

12. Text Book
O“Introduction to
Algorithms”, Thomas H.
Cormen, Charles E, Leiserson,
Ronald L. Rivest, Clifford Stein.
MIT Press, Third Edition

13. Algorithm History
OFirst used by Abu Ja’far Muhammed
Ibn Musa al-Khowarizmi (780-850)
OMember “house of wisdom” in
Baghdad
OOriginal word “algorism” and this
word evolved into Algorithm in
eighteen century

14. Algorithm History
OHis book “Hindu Numerals” is
basis of modern decimal
notation
OHe give the concept of “zero”
OWestern Europe first learned
Algebra from him
OAlgebra comes from al-jabr, part
of title of his book Kitab al-jabr
w’al Muquabala

15. Summary of Last Discussion
An algorithm is a concrete and
step by step solution of some
computational problem written in
pseudo code form which take a
value or (set of Values ) as input
and generate a value or (set of
Values ) as output

16. Algorithms (Pseudo-code)
f(n)
Input(n)
Output (n`)

17. Algorithms (Pseudo-code)
Algorithms are:
• Correct
• Algorithms are generic (Not
written for specific size and type
of input)

18. Introduction To The
Course

19. Introduction To The Course
1. Basic concepts
O Algorithm definition and importance in CS
O Analyzing Algorithm, Algorithm designing
O Growth of function Asymptotic Notation
O Recurrence and Mathematical Induction: The
substitution method, Recursion Tree Method, The Master
Method
2. Sorting
O Heapsort: Heap sort, maintaining a heap property,
Building a heap, the heap sort algorithm.
O Quicksort: Description of Quick sort, Performance of
Quick sort.
O Sorting in linear time: Lower bound for sorting,
Counting sort, Radix sort, Bucket sort.
3. Advance Design Techniques
O Dynamic Programming: Dynamic Programming,
Matrix Chain Multiplication, Knapsack Problem.
O Greedy Algorithm: Elements of Greedy Algorithm,
Huffman Code

20. Introduction To The Course
4. Graph Algorithms
O Elementary Graph Algorithm: Some concepts
about Graphs, Representation of graphs, Breath
First Search, Depth First Search, Topological
sort.
O Minimum Spanning Tree: Krushkal Algorithm,
Prims Algorithm.
O Single Source shortest Paths: Bellman Ford
Algorithm, Single Source Shortest paths in direct
acyclic graph, Dijkstra’s Algorithm.
O All Pairs shortest Paths: Floyd Warshall
Algorithm
5. NP-Complete Problems
O Polynomial time
O Polynomial time verification
O NP-completeness and reducibility

21. Importance of studying this
subject
OImproves problem solving skill
OGives mathematical foundations for
analyzing algorithms
OSelection among lots of candidate
solutions
OLearn good designing techniques
OCore area of computer science and
computer programming.

22. In the Last Lecture
ODefinition
ORepresentation of Algorithms
OPseudo-Code
OFlow Chart
OHistory
OCourse Introduction

23. Searching
OSearching an elements from array
(Linear Search)
OLinearSearch( Record[1…..n], m)

24. Searching
LinearSearch( Record[1…..n], m)
1. k=false
2. for I =1 to n
3. if Record[i]==m
4. K=true;
5. break;
6. if k==true
7. print “Element found”

25. Todays Agenda
OAnalysis of Algorithms
(Criteria)
OHow Efficient an Algorithm is
?
OUnderstanding Design and
Analysis ( A Selection
Problem )

26. Criterion for analyzing
Efficiency of Algorithm is measured in
terms of computation recourses
used:
O Running time (Most Often)
O Memory used
OEtc.
We should be agree on some
criterion

27. Mathematical Model of
computation
OAnalysis should be
independent
OArchitecture
OProgramming Language
OFor this we need to assume
an Architecture?

28. Random Access Machine
(RAM)
OSingle Process : Instruction
are executed one by one (not
parallelism)
OInfinitely large random access
memory

29. Writing Good Algorithms…
OUnderstand the problem
ODevelop Thinking habit
OThink Easy (Build on easy
solutions)

30. Design And Analysis
In order to understand design
and analysis procedure we will
do an example

31. Selection Problem
OSuppose you want to purchase a Laptop
OYou want to pick fastest Laptop
OBut fast Laptops are expensive
OYou cannot decide which one is more
important price or speed

32. Selection Problem
ODefinitely do not want a Laptop if
there is a another Laptop that is
both fast and cheaper
OWe say that fast cheap Laptops
“dominates” the slow expensive
OSo given a list of Laptops we
want those that are not
dominated by the other?

33. Criterion for selection
Two criterion for selection:
OSpeed
OPrice

34. Mathematical Model
O P is in two dimensional space and its coordinates are
P = (p.x , p.y)
(x,y)
O x is speed of Laptop
O y is negation of price
We can say about y
O High value of y mean cheap Laptop and low y means
Laptop is expensive
O A point p is said to be dominated by a point q if p.x
<= q.x and p.y <= q.y
O In an array of points (Laptops) P={p1,p2,p3,….,pn} a
maximal point is not dominated by any other point

35. Example
OGiven a set of point P={p1,p2,p3,….,pn }
output the maximal points
OThose points of P such that pi is not
dominated by any other point