PC
Uploaded byPérez Gutiérrez María Concepción
100 views

Ae1 20 21_class 1_structural models

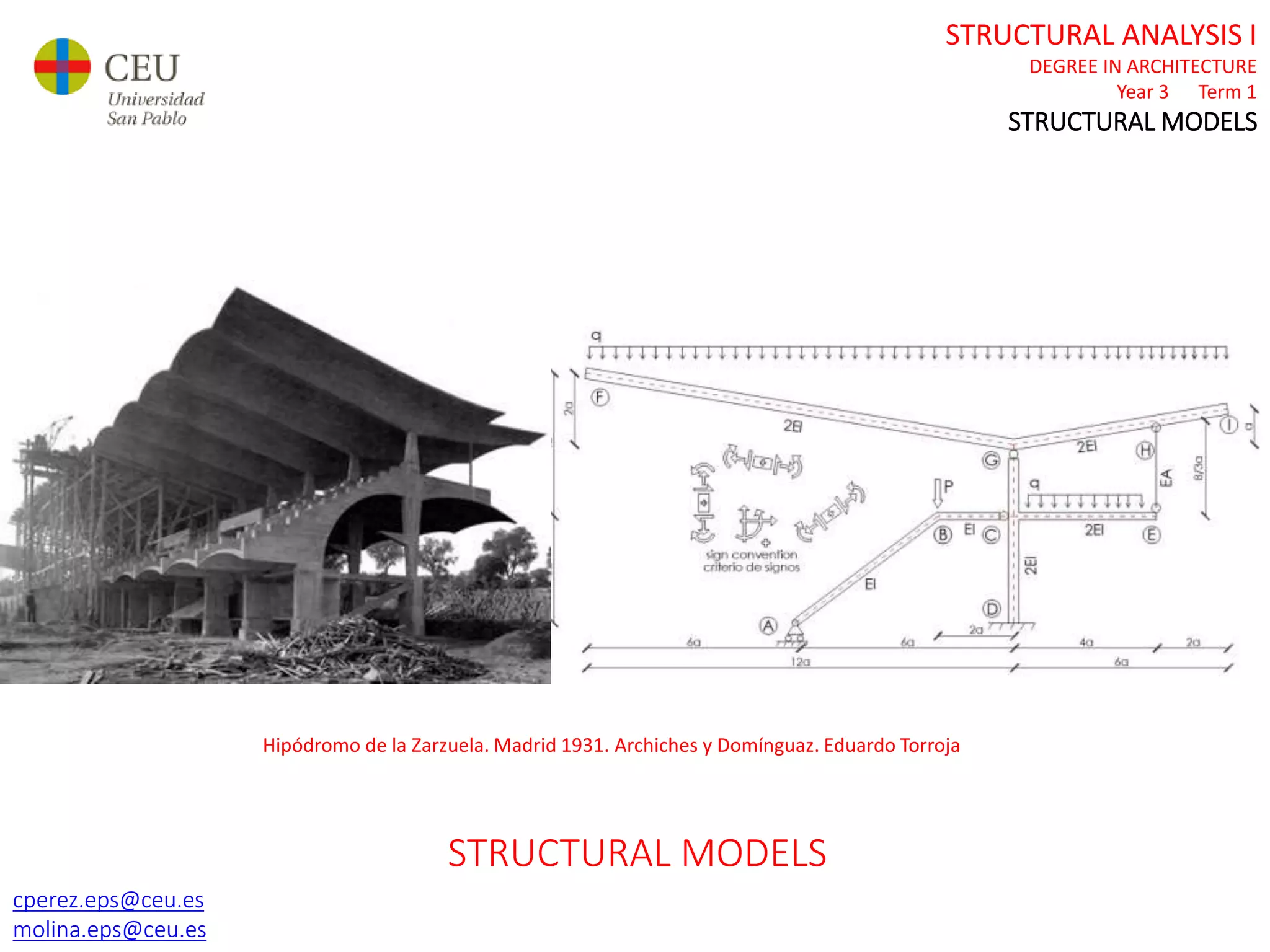
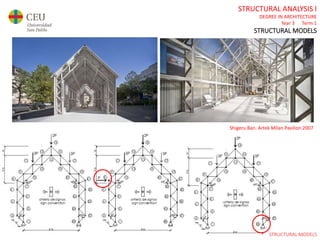
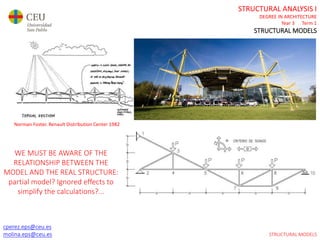
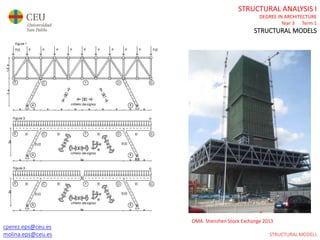
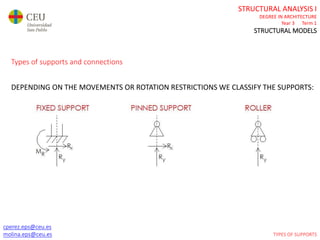
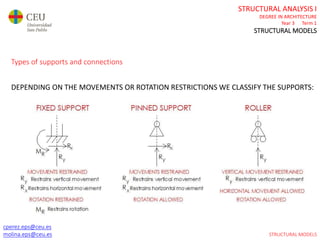
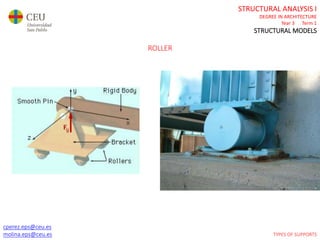
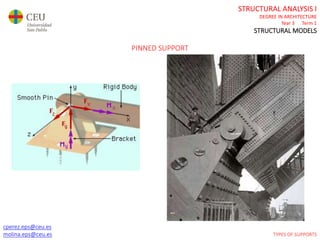
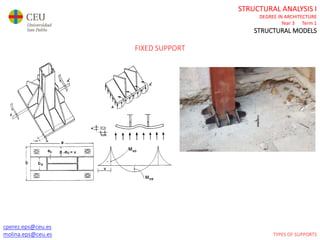
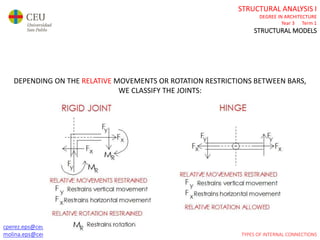
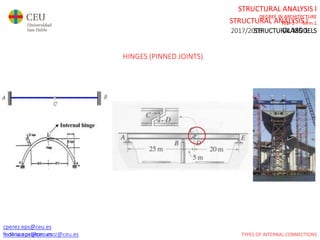
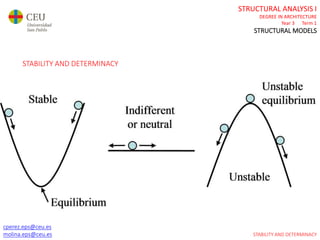
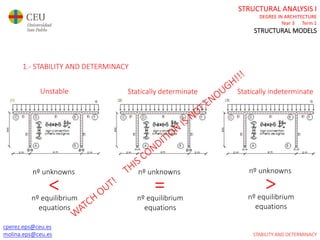
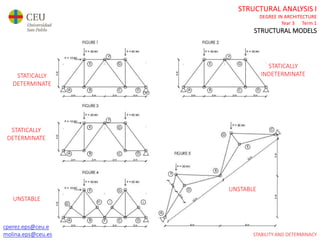
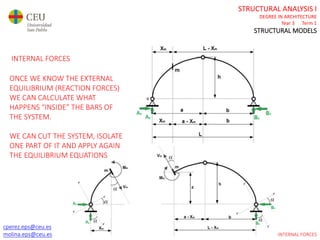
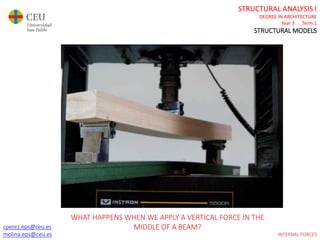
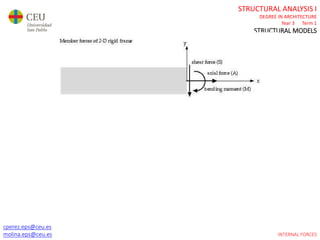
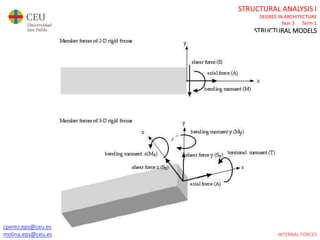
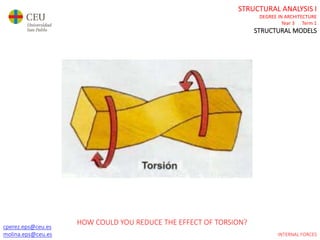
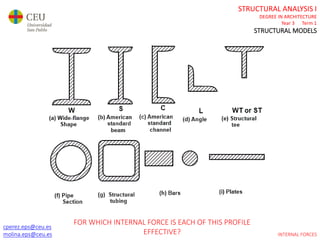
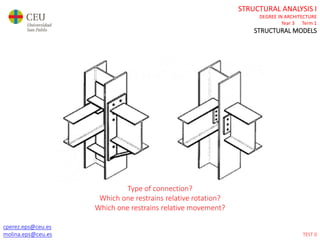
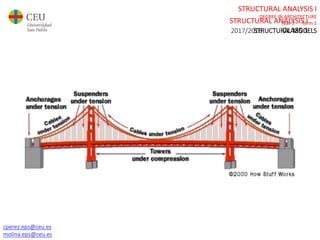
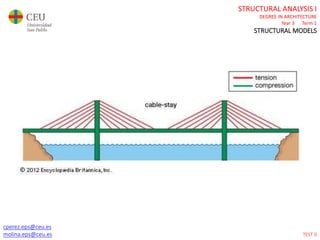
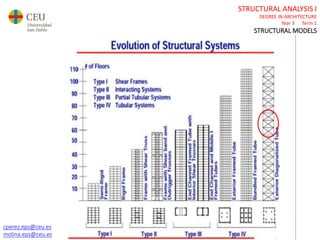
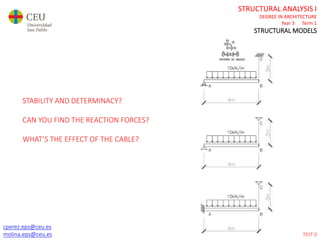
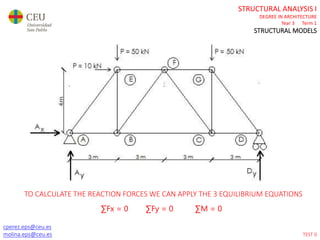
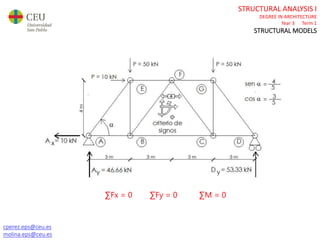
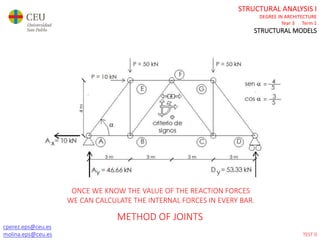
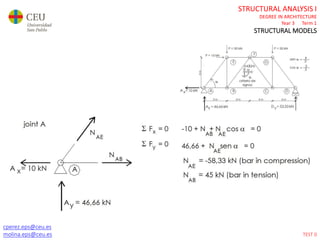
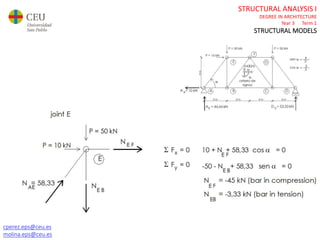
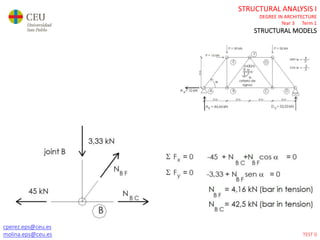
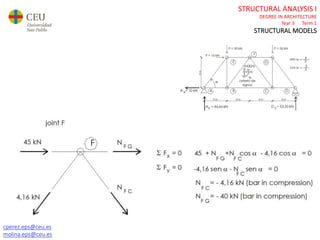
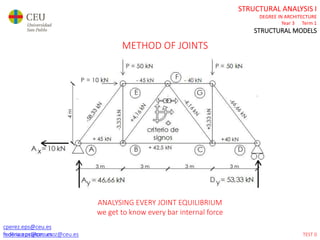
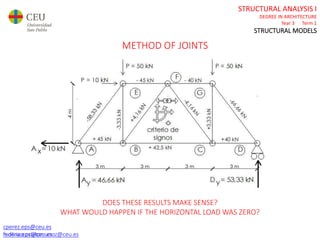
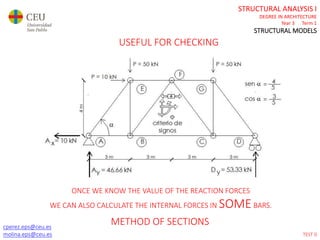
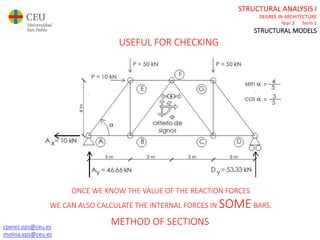
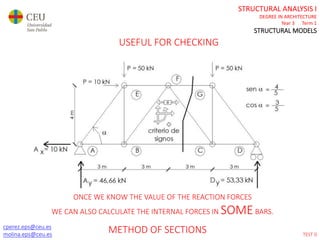
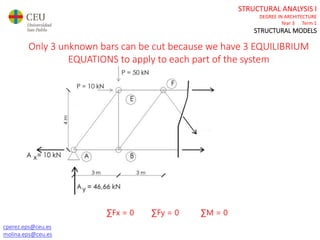
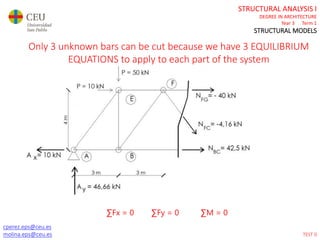
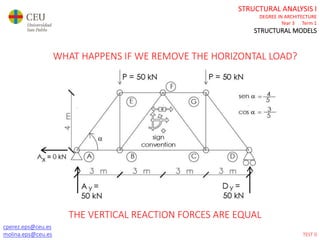
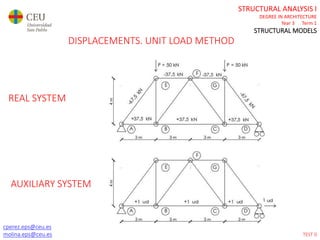
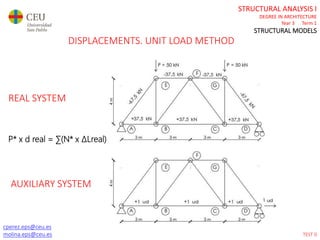
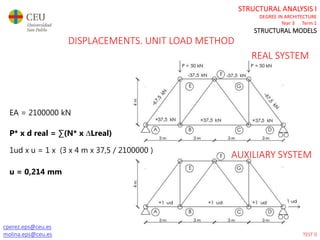
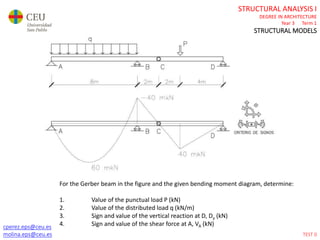
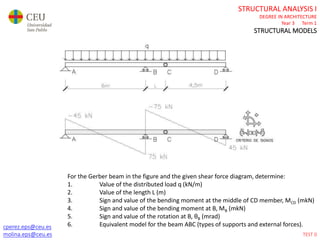
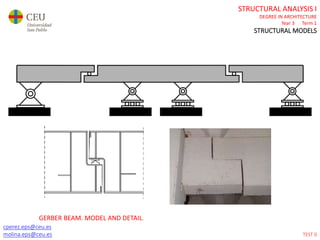
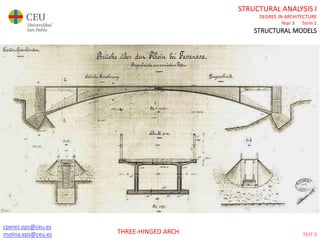
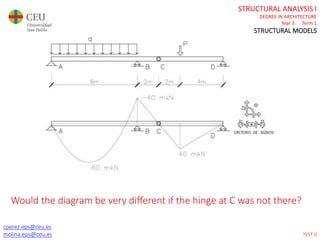
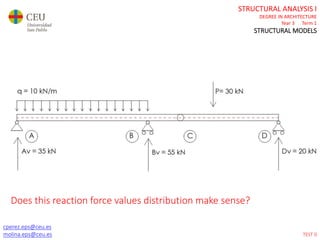
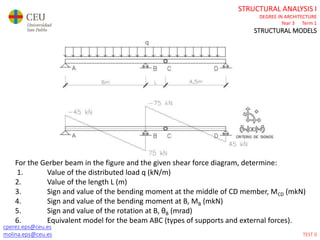
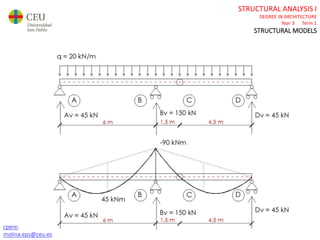
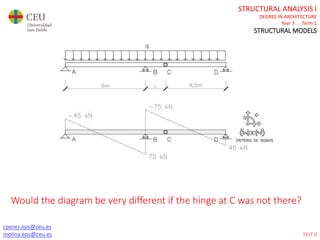
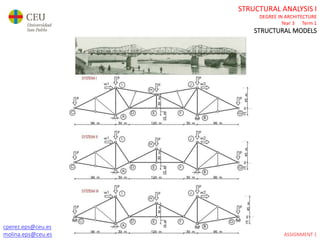
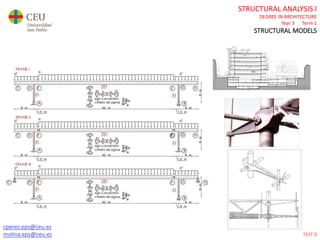
This document contains lecture slides for a Structural Analysis course. It discusses structural models, explaining that models are simplified representations of real structures used for calculations. It covers types of supports, loads, connections and joints in structural models. It also addresses structural stability, determinacy, and calculating internal forces like axial forces, shear forces, bending moments and torsion. Examples of structural models and buildings are provided throughout for illustration.

Embed presentation

cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Hipódromo de la Zarzuela. Madrid 1931. Archiches y Domínguaz. Eduardo Torroja STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es 2.- STABILITY AND STATICALLY DETERMINACY: REACTION FORCES 1.- STRUCTURAL MODELS: types of supports and connections types of loads bars geometry 5.- ASSIGNMENT 1 3.- INTERNAL FORCES: AXIAL FORCE SHEAR FORCE BENDING MOMENT TORSION 4.- TEST 0_year 19/20
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL MODELS WE DO NOTCALCULATE REAL STRUCTURES BUT MODELS OF THOSE REAL STRUCTURES
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Shigeru Ban. Artek Milan Pavilion 2007 STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es IT IS USELESS TO CALCULATE A MODEL IF IT DOES NOT BEHAVE AS THE REAL STRUCTURE STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Norman Foster. Renault Distribution Center 1982 WE MUST BE AWARE OF THE RELATIONSHIP BETWEEN THE MODEL AND THE REAL STRUCTURE: partial model? Ignored effects to simplify the calculations?... STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es IT IS VERY IMPORTANT TO UNDERSTAND HOW THE LOAD “TRAVELS” ALONG THE BUILDING STRUCTURAL SYSTEM and its effects EVERY LOAD SHOULD REACH THE GROUND
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es OMA. Shenzhen Stock Exchange 2013 STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es DEPENDING ON THE MOVEMENTS OR ROTATION RESTRICTIONS WE CLASSIFY THE SUPPORTS: Types of supports and connections TYPES OF SUPPORTS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es DEPENDING ON THE MOVEMENTS OR ROTATION RESTRICTIONS WE CLASSIFY THE SUPPORTS: Types of supports and connections STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es ROLLER TYPES OF SUPPORTS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es PINNED SUPPORT TYPES OF SUPPORTS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es FIXED SUPPORT TYPES OF SUPPORTS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es DEPENDING ON THE RELATIVE MOVEMENTS OR ROTATION RESTRICTIONS BETWEEN BARS, WE CLASSIFY THE JOINTS: TYPES OF INTERNAL CONNECTIONS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es HINGES (PINNED JOINTS) cperez.eps@ceu.es federico.prietomunoz@ceu.es STRUCTURAL ANALYSIS I 2017/2018 CLASS 1 TYPES OF INTERNAL CONNECTIONS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es RIGID (or FIXED JOINTS) STRUCTURAL ANALYSIS I 2017/2018 CLASS 1 TYPES OF INTERNAL CONNECTIONS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es STABILITY AND DETERMINACY A SYSTEM CAN BE CONSIDERED A STRUCTURE ONLY IF IT IS IN STABLE EQUILIBRIUM STABILITY AND DETERMINACY
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es STABILITY AND DETERMINACY STABILITY AND DETERMINACY
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es 1.- STABILITY AND DETERMINACY nº unknowns nº equilibrium equations < nº unknowns nº equilibrium equations = nº unknowns nº equilibrium equations > Unstable Statically determinate Statically indeterminate STABILITY AND DETERMINACY
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es STABILITY AND DETERMINACY STATICALLY INDETERMINATE STATICALLY DETERMINATE UNSTABLE STATICALLY DETERMINATE UNSTABLE
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES INTERNAL FORCES ONCE WE KNOW THE EXTERNAL EQUILIBRIUM (REACTION FORCES) WE CAN CALCULATE WHAT HAPPENS “INSIDE” THE BARS OF THE SYSTEM. WE CAN CUT THE SYSTEM, ISOLATE ONE PART OF IT AND APPLY AGAIN THE EQUILIBRIUM EQUATIONS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES THE FORCE IN THE DIRECTON OF THE BAR DIRECTRIX IS CALLED AXIAL FORCE
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES THE ROPE IS IN TENSION AND WHEN THE CHILDREN PULL IT GETS…. ¿LONGER OR SHORTER?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES THE PARTHENON INTERNAL COLUMNS ARE IN COMPRESSION THEY GET…. ¿LONGER OR SHORTER?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES BE CAREFUL WITH ELEMENTS UNDER COMPRESSION AND BUCKLING
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES IS THIS WAY OF BREAKING BREAD EASY? WHY?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES THE EFFECT OF THE SHEAR FORCE IS…
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES WHAT HAPPENS WHEN WE APPLY A VERTICAL FORCE IN THE MIDDLE OF A BEAM?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES HOW COULD YOU REDUCE DE VERTICAL DISPLACEMENT IN THE MIDDLE OF THE SPAN?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES WHAT WOULD HAPPEN IF ALL THE PEOPLE DECIDE TO MOVE TOWARS ONE SIDE OF THE BRIDGE?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES HOW COULD YOU REDUCE THE EFFECT OF TORSION?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es INTERNAL FORCES FOR WHICH INTERNAL FORCE IS EACH OF THIS PROFILE EFFECTIVE?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Type of connection? Which one restrains relative rotation? Which one restrains relative movement? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Type of connection? Does any of them allow movement or rotation? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Type of connection? What happens with the bending moments and the end bar moments? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es cperez.eps@ceu.es federico.prietomunoz@ceu.es San Francisco Suspension Bridge. Built in 1937 TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I 2017/2018 CLASS 1
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es CAN YOU TELL THE DIFFERENCE BETWEEN A SUSPENSION BRIDGE AND A CABLE-STAYED BRIDGE? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Puente de Rande cable-stayed Bridge. Vigo 1973 TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Vigo cable-stayed Bridge
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Chicago John Hancock Tower 1970 TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Chicago Lake Shore Drive Apartments. Mies van der Rohe TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es John Hancock Center (1970): Architectural height 1128’ (344 m), 100 stories. Plan dimensions at the ground floor: 262x164’ (78,6x49,2 m). Plan dimensions at the top floor: 160x100’ (48x30 m). Chicago John Hancock Tower 1970
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Chicago John Hancock Tower 1970
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Miralles-Tagliabue. Santa Caterina Market. Barcelona 1997 / 2005 TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es REMEMBER IT IS VERY IMPORTANT TO UNDERSTAND HOW THE LOAD TRAVELS ALONG THE BUILDING STRUCTURAL SYSTEM. EVERY LOAD SHOULD REACH THE GROUND
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es Santa Caterina Market (1997/2005): Central frame span: 42 m. Roof weight: 92 kp/m2. 7 concrete supports with cross section 90 cm x 90 cm. 2 post tensioned beams with spans of 12-22 m and cantilever from 4-10 m, cross section beam depth 1,2 m. Archs of 6 m height. V shaped beams average 50 m span. Wooden Arches and Ribs coming from the original market structure in a 50%. TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es STABILITY AND DETERMINACY? CAN YOU FIND THE REACTION FORCES? WHAT’S THE EFFECT OF THE CABLE? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS SIMPLE TRUSSES THE CALCULATION OF DISPLACEMENTS IF WE DO NOT APPLY THE UNIT LOAD METHOD IS REALLY TIRING… TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS TO CALCULATE THE REACTION FORCES WE CAN APPLY THE 3 EQUILIBRIUM EQUATIONS ∑Fx = 0 ∑Fy = 0 ∑M = 0 TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS ∑Fx = 0 ∑Fy = 0 ∑M = 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS ONCE WE KNOW THE VALUE OF THE REACTION FORCES WE CAN CALCULATE THE INTERNAL FORCES IN EVERY BAR. METHOD OF JOINTS TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es federico.prietomunoz@ceu.es METHOD OF JOINTS ANALYSING EVERY JOINT EQUILIBRIUM we get to know every bar internal force TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es federico.prietomunoz@ceu.es METHOD OF JOINTS DOES THESE RESULTS MAKE SENSE? WHAT WOULD HAPPEN IF THE HORIZONTAL LOAD WAS ZERO?
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS ONCE WE KNOW THE VALUE OF THE REACTION FORCES WE CAN ALSO CALCULATE THE INTERNAL FORCES IN SOMEBARS. METHOD OF SECTIONS USEFUL FOR CHECKING TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS ONCE WE KNOW THE VALUE OF THE REACTION FORCES WE CAN ALSO CALCULATE THE INTERNAL FORCES IN SOMEBARS. METHOD OF SECTIONS USEFUL FOR CHECKING
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS ONCE WE KNOW THE VALUE OF THE REACTION FORCES WE CAN ALSO CALCULATE THE INTERNAL FORCES IN SOMEBARS. METHOD OF SECTIONS USEFUL FOR CHECKING TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS Only 3 unknown bars can be cut because we have 3 EQUILIBRIUM EQUATIONS to apply to each part of the system ∑Fx = 0 ∑Fy = 0 ∑M = 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS Only 3 unknown bars can be cut because we have 3 EQUILIBRIUM EQUATIONS to apply to each part of the system ∑Fx = 0 ∑Fy = 0 ∑M = 0 TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS DISPLACEMENTS ONCE WE KNOW THE VALUE OF THE INTERNAL FORCES WE CAN CALCULATE THE DISPLACEMENTS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS THE VERTICAL REACTION FORCES ARE EQUAL WHAT HAPPENS IF WE REMOVE THE HORIZONTAL LOAD? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS DISPLACEMENTS. UNIT LOAD METHOD REAL SYSTEM AUXILIARY SYSTEM TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS DISPLACEMENTS. UNIT LOAD METHOD REAL SYSTEM AUXILIARY SYSTEM P* x d real = ∑(N* x ∆Lreal) TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS DISPLACEMENTS. UNIT LOAD METHOD REAL SYSTEM AUXILIARY SYSTEM EA = 2100000 kN P* x d real = ∑(N* x ∆Lreal) 1ud x u = 1 x (3 x 4 m x 37,5 / 2100000 ) u = 0,214 mm TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es For the Gerber beam in the figure and the given bending moment diagram, determine: 1. Value of the punctual load P (kN) 2. Value of the distributed load q (kN/m) 3. Sign and value of the vertical reaction at D, Dy (kN) 4. Sign and value of the shear force at A, VA (kN) TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS cperez.eps@ceu.es molina.eps@ceu.es For the Gerber beam in the figure and the given shear force diagram, determine: 1. Value of the distributed load q (kN/m) 2. Value of the length L (m) 3. Sign and value of the bending moment at the middle of CD member, MCD (mkN) 4. Sign and value of the bending moment at B, MB (mkN) 5. Sign and value of the rotation at B, θB (mrad) 6. Equivalent model for the beam ABC (types of supports and external forces). TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS GERBER BEAM BRIDGE. Kuma Village. Japan TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS GERBER BEAM. MODEL AND DETAIL. TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS THREE-HINGED ARCH TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS THREE-HINGED ARCH
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS Would the diagram be very different if the hinge at C was not there? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS Does this reaction force values distribution make sense? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS For the Gerber beam in the figure and the given shear force diagram, determine: 1. Value of the distributed load q (kN/m) 2. Value of the length L (m) 3. Sign and value of the bending moment at the middle of CD member, MCD (mkN) 4. Sign and value of the bending moment at B, MB (mkN) 5. Sign and value of the rotation at B, θB (mrad) 6. Equivalent model for the beam ABC (types of supports and external forces). TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS Would the diagram be very different if the hinge at C was not there? TEST 0
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS ASSIGNMENT 1
cperez.eps@ceu.es molina.eps@ceu.es STRUCTURAL ANALYSIS I DEGREE IN ARCHITECTURE Year 3 Term 1 STRUCTURAL MODELS TEST 0

More Related Content

PPTX
Ae1 21 22_class 5_10_08_slope deflection_2
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_test 2
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_class 5_10_16
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_class 7_slope deflection_side sway
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_sb_s_frame with and without cantilevers
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 19 20_class 2_09_10
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1920 class 5_10_8
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1920 class 4_10_03
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 5_10_08_slope deflection_2
byPérez Gutiérrez María Concepción
 
Ae1 20 21_test 2
byPérez Gutiérrez María Concepción
 
Ae1 20 21_class 5_10_16
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 7_slope deflection_side sway
byPérez Gutiérrez María Concepción
 
Ae1 21 22_sb_s_frame with and without cantilevers
byPérez Gutiérrez María Concepción
 
Ae1 19 20_class 2_09_10
byPérez Gutiérrez María Concepción
 
Ae1 1920 class 5_10_8
byPérez Gutiérrez María Concepción
 
Ae1 1920 class 4_10_03
byPérez Gutiérrez María Concepción
 

What's hot

PPTX
Ae1 21 22_class 0_structural models
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_class 2_statically determinate systems_examples
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_class 3_statically indeterminate_class
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_class 0_07_09_21
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_test 3
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 19 20_2_test 2
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_class 8_matrix
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 6_10_03
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1920 class 3_09_13
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_test 3_slope deflection_2
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 19 20_2_test 1
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_class 7_slope deflection_side sway
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_test 2_slope deflection_1
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_sb_s_semi frames_slope deflection_settlements_side sway
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 7_10_10
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 1_09_05
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1920 class 1_09_06
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 21 22_test 1_comp
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 18 !9_sb_s_frame_inclined supports and cantilever
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 8_10_16
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 0_structural models
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 2_statically determinate systems_examples
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 3_statically indeterminate_class
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 0_07_09_21
byPérez Gutiérrez María Concepción
 
Ae1 20 21_test 3
byPérez Gutiérrez María Concepción
 
Ae1 19 20_2_test 2
byPérez Gutiérrez María Concepción
 
Ae1 21 22_class 8_matrix
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 6_10_03
byPérez Gutiérrez María Concepción
 
Ae1 1920 class 3_09_13
byPérez Gutiérrez María Concepción
 
Ae1 21 22_test 3_slope deflection_2
byPérez Gutiérrez María Concepción
 
Ae1 19 20_2_test 1
byPérez Gutiérrez María Concepción
 
Ae1 20 21_class 7_slope deflection_side sway
byPérez Gutiérrez María Concepción
 
Ae1 21 22_test 2_slope deflection_1
byPérez Gutiérrez María Concepción
 
Ae1 21 22_sb_s_semi frames_slope deflection_settlements_side sway
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 7_10_10
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 1_09_05
byPérez Gutiérrez María Concepción
 
Ae1 1920 class 1_09_06
byPérez Gutiérrez María Concepción
 
Ae1 21 22_test 1_comp
byPérez Gutiérrez María Concepción
 
Ae1 18 !9_sb_s_frame_inclined supports and cantilever
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 8_10_16
byPérez Gutiérrez María Concepción
 

Similar to Ae1 20 21_class 1_structural models

PPTX
AE1_22_23_CLASS 1__22_09_12_STRUCTURAL MODELS.pptx
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 2_09_12
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS 2_22_09_15_STATICALLY DETERMINATE SYSTEMS_EXAMPLES.pptx
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_class 2_statically determinate systems_examples
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1920 class 6_10_15
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 5_09_26
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_class 0_18_09_20
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 3_09_19_
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 19 20_1_beam with cantilvers
byPérez Gutiérrez María Concepción
 
PPTX
AE1_18_19_class 0
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS 3_22_09_19_STATICALLY INDETERMINATE_class.pptx
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1718 class 1_09_12
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS 0_22_09_08.pptx
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_test 1
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 4_09_25
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS 3_22_09_22_STATICALLY INDETERMINATE_class 2.pptx
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 20 21_class 3_09_29_statically indeterminate
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS 6_22_10_06_STATICALLY INDETERMINATE_class 4.pptx
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1718 class 2_09_19
byPérez Gutiérrez María Concepción
 
PPTX
Ae1 1819 class 9_11_6
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 1__22_09_12_STRUCTURAL MODELS.pptx
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 2_09_12
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 2_22_09_15_STATICALLY DETERMINATE SYSTEMS_EXAMPLES.pptx
byPérez Gutiérrez María Concepción
 
Ae1 20 21_class 2_statically determinate systems_examples
byPérez Gutiérrez María Concepción
 
Ae1 1920 class 6_10_15
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 5_09_26
byPérez Gutiérrez María Concepción
 
Ae1 20 21_class 0_18_09_20
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 3_09_19_
byPérez Gutiérrez María Concepción
 
Ae1 19 20_1_beam with cantilvers
byPérez Gutiérrez María Concepción
 
AE1_18_19_class 0
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 3_22_09_19_STATICALLY INDETERMINATE_class.pptx
byPérez Gutiérrez María Concepción
 
Ae1 1718 class 1_09_12
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 0_22_09_08.pptx
byPérez Gutiérrez María Concepción
 
Ae1 20 21_test 1
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 4_09_25
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 3_22_09_22_STATICALLY INDETERMINATE_class 2.pptx
byPérez Gutiérrez María Concepción
 
Ae1 20 21_class 3_09_29_statically indeterminate
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 6_22_10_06_STATICALLY INDETERMINATE_class 4.pptx
byPérez Gutiérrez María Concepción
 
Ae1 1718 class 2_09_19
byPérez Gutiérrez María Concepción
 
Ae1 1819 class 9_11_6
byPérez Gutiérrez María Concepción
 

More from Pérez Gutiérrez María Concepción

PPTX
FM1_geo_1_22_12_13.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_12_12.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_11_29.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_11_29.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_11_28.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_11_22.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_11_21.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_11_21.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_24_11_15.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_24_11_14.pptx
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS_MATRIX.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_24_11_8.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_24_11_7.pptx
byPérez Gutiérrez María Concepción
 
PPTX
AE1_21_22_TEST 3_SLOPE DEFLECTION_2.pptx
byPérez Gutiérrez María Concepción
 
PPTX
AE1_11_22_frame competition.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_24_10_25.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_24_10_24.pptx
byPérez Gutiérrez María Concepción
 
PPTX
AE1_22_23_CLASS 9_22_10_20_STATICALLY INDETERMINATE_class 4.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_10_18.pptx
byPérez Gutiérrez María Concepción
 
PPTX
FM1_geo_1_22_10_17.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_12_13.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_12_12.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_11_29.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_11_29.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_11_28.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_11_22.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_11_21.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_11_21.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_24_11_15.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_24_11_14.pptx
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS_MATRIX.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_24_11_8.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_24_11_7.pptx
byPérez Gutiérrez María Concepción
 
AE1_21_22_TEST 3_SLOPE DEFLECTION_2.pptx
byPérez Gutiérrez María Concepción
 
AE1_11_22_frame competition.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_24_10_25.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_24_10_24.pptx
byPérez Gutiérrez María Concepción
 
AE1_22_23_CLASS 9_22_10_20_STATICALLY INDETERMINATE_class 4.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_10_18.pptx
byPérez Gutiérrez María Concepción
 
FM1_geo_1_22_10_17.pptx
byPérez Gutiérrez María Concepción
 

Recently uploaded

PPTX
Wind Farm by Nishan Singha(Mintech).pptx
bynishansingha365
 
PDF
TechRush Hackathon 2026: A Platform for Innovation, Learning, and Real-World ...
byreshmi7103
 
PPTX
Presentation - Build AI Agents (gdgoc event).pptx
byvenkatahemanth42d
 
PDF
EDIH TRAINING AI FOR COMPANIES: MODULE 4
byHristian Daskalov
 
PDF
Earths-Structure-and-Composition_20260127_110958_0000.pdf
byabdurasabarfaki
 
PPTX
TechSprint WinterHack || After an intense hackathon filled with creativity, ...
bybajpaitusharoffon678
 
PDF
Formality - Logic Equivalence Checking - Part 2
byAmr Adel
 
PPTX
What TPM Looks Like When You’re Short-Staffed and Still Make It Work | Lean T...
byMaintWiz Technologies Private Limited
 
PDF
Julian Kalac -GEN AI inventive solution Automated SOC Report Processing .pdf
byJulian Kalac P.Eng
 
PDF
RVV Basic Terms and Analogy - (en/zhTW) - DannyJiang
byDanny Jiang
 
PDF
Process Scheduling Scheduling Queue, Types of Sheduler
bySanjay Gunjal
 
PDF
5.5 Inch 4K TFT LCD Display 3840×2160 UHD Panel – LS055D1SX05(G)
bySyluxdisplay
 
PDF
Taykon Proses -ENG- Process Equipment Manufacturer
byTAYKON
 
PDF
TRUSTWORTHY AI: BUILDING SAFE AND ETHICAL MACHINE LEARNING SYSTEMS
byAdri Jovin
 
PPTX
Explore how AI-powered maintenance checklists transform asset reliability and...
byMaintWiz Technologies Private Limited
 
PDF
PROBLEM SLOVING AND PYTHON PROGRAMMING UNIT 2.pdf
byA R SIVANESH M.E., QIP-PG (Cyber Security)., (Ph.D)
 
PPTX
MicroAccelerometers & microfluidics.pptx
byThamizhvani TR
 
PDF
FPGA Fabric and Synthesis All Parts Combined
byAmr Adel
 
PPTX
Tips for Designing Flex Circuits for Medical Applications
byEpec Engineered Technologies
 
PPTX
The Half-Life of Preventive Maintenance: Why PM Compliance Fails & How to Res...
byMaintWiz Technologies Private Limited
 
Wind Farm by Nishan Singha(Mintech).pptx
bynishansingha365
 
TechRush Hackathon 2026: A Platform for Innovation, Learning, and Real-World ...
byreshmi7103
 
Presentation - Build AI Agents (gdgoc event).pptx
byvenkatahemanth42d
 
EDIH TRAINING AI FOR COMPANIES: MODULE 4
byHristian Daskalov
 
Earths-Structure-and-Composition_20260127_110958_0000.pdf
byabdurasabarfaki
 
TechSprint WinterHack || After an intense hackathon filled with creativity, ...
bybajpaitusharoffon678
 
Formality - Logic Equivalence Checking - Part 2
byAmr Adel
 
What TPM Looks Like When You’re Short-Staffed and Still Make It Work | Lean T...
byMaintWiz Technologies Private Limited
 
Julian Kalac -GEN AI inventive solution Automated SOC Report Processing .pdf
byJulian Kalac P.Eng
 
RVV Basic Terms and Analogy - (en/zhTW) - DannyJiang
byDanny Jiang
 
Process Scheduling Scheduling Queue, Types of Sheduler
bySanjay Gunjal
 
5.5 Inch 4K TFT LCD Display 3840×2160 UHD Panel – LS055D1SX05(G)
bySyluxdisplay
 
Taykon Proses -ENG- Process Equipment Manufacturer
byTAYKON
 
TRUSTWORTHY AI: BUILDING SAFE AND ETHICAL MACHINE LEARNING SYSTEMS
byAdri Jovin
 
Explore how AI-powered maintenance checklists transform asset reliability and...
byMaintWiz Technologies Private Limited
 
PROBLEM SLOVING AND PYTHON PROGRAMMING UNIT 2.pdf
byA R SIVANESH M.E., QIP-PG (Cyber Security)., (Ph.D)
 
MicroAccelerometers & microfluidics.pptx
byThamizhvani TR
 
FPGA Fabric and Synthesis All Parts Combined
byAmr Adel
 
Tips for Designing Flex Circuits for Medical Applications
byEpec Engineered Technologies
 
The Half-Life of Preventive Maintenance: Why PM Compliance Fails & How to Res...
byMaintWiz Technologies Private Limited
 

Ae1 20 21_class 1_structural models