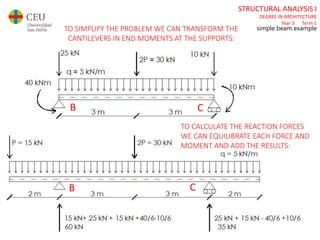
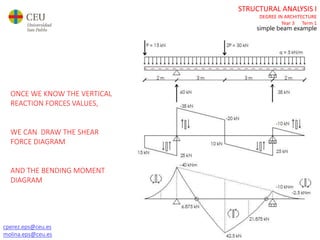
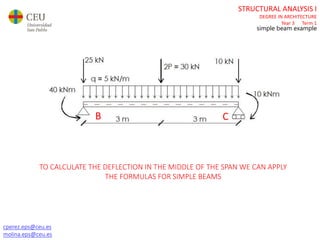
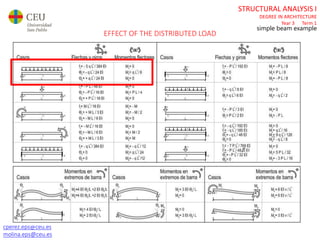
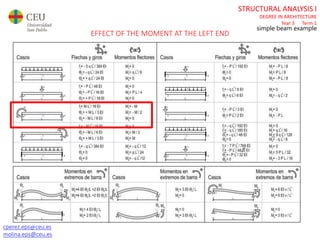
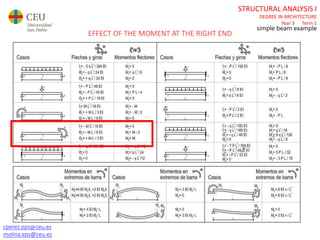
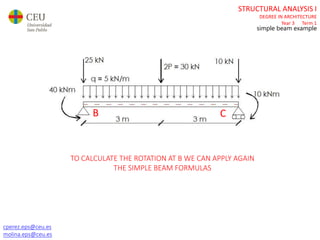
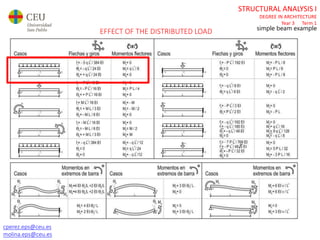
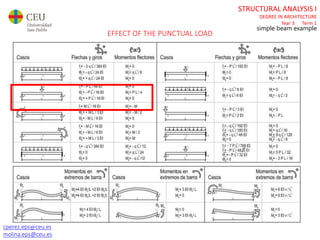
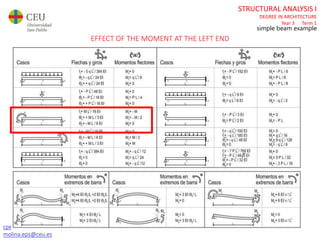
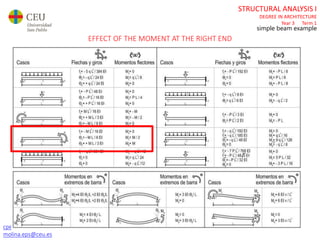
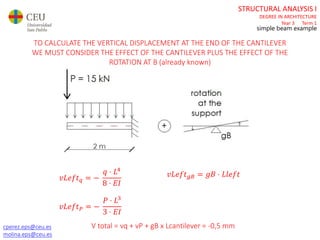
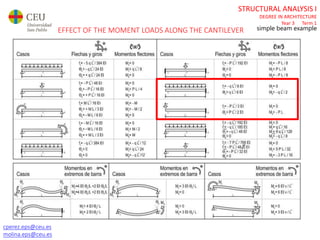
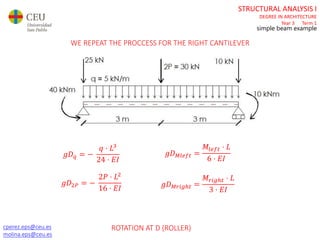
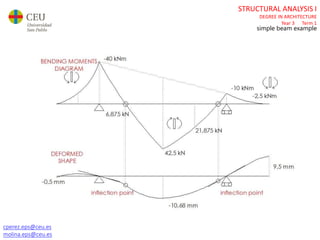
The document discusses analyzing a beam with one central span and two cantilevers. It describes transforming the cantilevers into end moments at the supports to simplify the problem. It then calculates the reaction forces and draws the shear force and bending moment diagrams. Deflections and rotations are calculated at various points along the beam using formulas for simple beams. The effects of distributed, punctual, and moment loads are considered. Deflections and rotations are calculated at the left and right ends of the cantilevers using a similar process.

1. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
LET’S ANALYZE THIS BEAM WITH ONE SPAN AND TWO CANTILEVERS
As it is not symmetrical, the vertical reaction forces at A and B
are not going to be equal
B C

2. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
B C
B C
TO SIMPLIFY THE PROBLEM WE CAN TRANSFORM THE
CANTILEVERS IN END MOMENTS AT THE SUPPORTS:
TO CALCULATE THE REACTION FORCES
WE CAN EQUILIBRATE EACH FORCE AND
MOMENT AND ADD THE RESULTS:

3. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
ONCE WE KNOW THE VERTICAL
REACTION FORCES VALUES,
WE CAN DRAW THE SHEAR
FORCE DIAGRAM
AND THE BENDING MOMENT
DIAGRAM

4. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
TO CALCULATE THE DEFLECTION IN THE MIDDLE OF THE SPAN WE CAN APPLY
THE FORMULAS FOR SIMPLE BEAMS
B C

5. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE DISTRIBUTED LOAD

6. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam exampleEFFECT OF THE PUNCTUAL LOAD

7. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE MOMENT AT THE LEFT END

8. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE MOMENT AT THE RIGHT END

9. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
𝑣 𝑞 = −
5 ⋅ 𝑞 ⋅ 𝐿4
384 ⋅ 𝐸𝐼
𝑣2𝑃 = −
2𝑃 ⋅ 𝐿3
48 ⋅ 𝐸𝐼
𝑣 𝑀𝑙𝑒𝑓𝑡 =
𝑀𝑙𝑒𝑓𝑡 ⋅ 𝐿2
16 ⋅ 𝐸𝐼
𝑣 𝑀𝑟𝑖𝑔ℎ𝑡 =
𝑀𝑟𝑖𝑔ℎ𝑡 ⋅ 𝐿2
16 ⋅ 𝐸𝐼
DEFLECTION IN THE MIDDLE OF THE SPAN
V total = vq + vP + vMleft + vMright = -10,68 mm
Beam bending stiffness: EI = 10000 kNm2

10. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
TO CALCULATE THE ROTATION AT B WE CAN APPLY AGAIN
THE SIMPLE BEAM FORMULAS
B C

11. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE DISTRIBUTED LOAD

12. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE PUNCTUAL LOAD

13. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE MOMENT AT THE LEFT END

14. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
EFFECT OF THE MOMENT AT THE RIGHT END

15. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
𝑔𝐵𝑞 = −
𝑞 ⋅ 𝐿3
24 ⋅ 𝐸𝐼
𝑔𝐵2𝑃 = −
2𝑃 ⋅ 𝐿2
16 ⋅ 𝐸𝐼
𝑔𝐵 𝑀𝑙𝑒𝑓𝑡 =
𝑀𝑙𝑒𝑓𝑡 ⋅ 𝐿
3 ⋅ 𝐸𝐼
𝑔𝐵 𝑀𝑟𝑖𝑔ℎ𝑡 =
𝑀𝑟𝑖𝑔ℎ𝑡 ⋅ 𝐿
6 ⋅ 𝐸𝐼
B C
gB total = gBq + gBP + gB Mleft + gB Mright = -4,275 mrad
Beam bending stiffness: EI = 10000 kNm2

16. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
𝑣𝐿𝑒𝑓𝑡 𝑞 = −
𝑞 ⋅ 𝐿4
8 ⋅ 𝐸𝐼
𝑣𝐿𝑒𝑓𝑡 𝑃 = −
𝑃 ⋅ 𝐿3
3 ⋅ 𝐸𝐼
𝑣𝐿𝑒𝑓𝑡 𝑔𝐵 = 𝑔𝐵 ⋅ 𝐿𝑙𝑒𝑓𝑡
TO CALCULATE THE VERTICAL DISPLACEMENT AT THE END OF THE CANTILEVER
WE MUST CONSIDER THE EFFECT OF THE CANTILEVER PLUS THE EFFECT OF THE
ROTATION AT B (already known)
V total = vq + vP + gB x Lcantilever = -0,5 mm

17. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam exampleEFFECT OF THE MOMENT LOADS ALONG THE CANTILEVER

18. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
𝑔𝐷 𝑞 = −
𝑞 ⋅ 𝐿3
24 ⋅ 𝐸𝐼
𝑔𝐷2𝑃 = −
2𝑃 ⋅ 𝐿2
16 ⋅ 𝐸𝐼
𝑔𝐷 𝑀𝑙𝑒𝑓𝑡 =
𝑀𝑙𝑒𝑓𝑡 ⋅ 𝐿
6 ⋅ 𝐸𝐼
𝑔𝐷 𝑀𝑟𝑖𝑔ℎ𝑡 =
𝑀𝑟𝑖𝑔ℎ𝑡 ⋅ 𝐿
3 ⋅ 𝐸𝐼
ROTATION AT D (ROLLER)
WE REPEAT THE PROCCESS FOR THE RIGHT CANTILEVER

19. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example
𝑣𝑅𝑖𝑔ℎ𝑡 𝑞 = −
𝑞 ⋅ 𝐿4
8 ⋅ 𝐸𝐼
𝑣𝑅𝑖𝑔ℎ𝑡 𝑔𝐷 = 𝑔𝐵 ⋅ 𝐿𝑙𝑒𝑓𝑡
VERTICAL DISPLACEMENT AT THE END OF THE CANTILEVER
WE REPEAT THE PROCCESS FOR THE RIGHT CANTILEVER
V total = vq + vP + gD x Lcantilever = +9,5 mm

20. cperez.eps@ceu.es
molina.eps@ceu.es
STRUCTURAL ANALYSIS I
DEGREE IN ARCHITECTURE
Year 3 Term 1
simple beam example