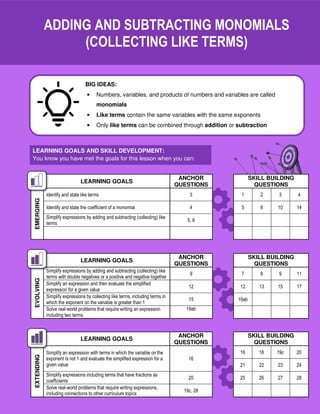
The document focuses on the concepts of adding and subtracting monomials by collecting like terms. It outlines learning goals, big ideas, and skill development questions, including the evaluation of expressions and solving real-world problems. The document provides numerous examples and exercises aimed at reinforcing these mathematical skills.

1. Adding and Subtracting Monomials (Collecting Like Terms)
LEARNING GOALS
ANCHOR
QUESTIONS
SKILL BUILDING
QUESTIONS
EXTENDING
Simplify an expression with terms in which the variable on the
exponent is not 1 and evaluate the simplified expression for a
given value
16
16 18 19c 20
21 22 23 24
Simplify expressions including terms that have fractions as
coefficients
20 25 26 27 28
Solve real-world problems that require writing expressions,
including connections to other curriculum topics
19c, 28
ADDING AND SUBTRACTING MONOMIALS
(COLLECTING LIKE TERMS)
BIG IDEAS:
• Numbers, variables, and products of numbers and variables are called
monomials
• Like terms contain the same variables with the same exponents
• Only like terms can be combined through addition or subtraction
LEARNING GOALS AND SKILL DEVELOPMENT:
You know you have met the goals for this lesson when you can:
LEARNING GOALS
ANCHOR
QUESTIONS
SKILL BUILDING
QUESTIONS
EMERGING
Identify and state like terms 3 1 2 3 4
Identify and state the coefficient of a monomial 4 5 6 10 14
Simplify expressions by adding and subtracting (collecting) like
terms
5, 6
LEARNING GOALS
ANCHOR
QUESTIONS
SKILL BUILDING
QUESTIONS
EVOLVING
Simplify expressions by adding and subtracting (collecting) like
terms with double negatives or a positive and negative together
9 7 8 9 11
Simplify an expression and then evaluate the simplified
expression for a given value
12 12 13 15 17
Simplify expressions by collecting like terms, including terms in
which the exponent on the variable is greater than 1
15 19ab
Solve real-world problems that require writing an expression
including two terms
19ab

2. Adding and Subtracting Monomials (Collecting Like Terms)
BUILD YOUR SKILLS
1. State the value that should be placed in each box.
a) b)
c) d)
2. State the value that should be placed in each box.
a)
b)
c)
3. Identify each of the following pairs as like terms or unlike terms.
a) 6x and 14x b) 10x and 10y c) 5a
− and 10a d) 9x
− and 5
4. State the coefficient for each of the following terms.
a) 8x b) 15y c) 4x
− d) x e) y
−
5. Simplify each of the following expressions by collecting like terms.
a) x x x x
+ + + b) 2 5
y y
+ c) 3 4
x x x
+ + d) 9 5 4
a a a
− +
e) 2 6 8
x x x
+ − f) 3 7
k k
− g) 5 9
w w w
+ − h) 2 10 7
z z z
− +
6. Simplify each of the following expressions by collecting like terms.
a) x x y y y
+ + + + b) 2 5 6 10
a a b b
+ + + c) 3 10 4 3
g h g h
+ + +
d) 10 8 4 3
c d c d
+ − − e) 5 2 8
x y x y
+ − − f) 6 4 6 3 2
m m n m n
− + − −
7. Shagun stated that 5 2
x + is equal to 7x . Is Shagun’s claim correct? Explain.
2 3 2
4
7 4 3 5

3. Adding and Subtracting Monomials (Collecting Like Terms)
8. Kalani and Marc were asked to simplify the expression 9 3 4 10
x x
+ − − by collecting like terms.
Kalani’s answer was 5 ( 7)
x + − and Marc’s answer was 5 7
x − . Was Kalani correct? Was Marc
correct? Explain.
9. Express each of the following without using brackets.
a) 8 ( 3)
x + − b) 4 ( 6)
x
− − − c) 8 ( 4 )
x y
+ − d) 9 ( 4 )
a b
− − −
10. Simplify each of the following expressions by collecting like terms.
a) 2 5 6 8
x x
+ + + b) 7 3 4 2
x x
+ + + c) 8 10 4 12
p p
− + +
d) 5 8 6 10
y y
− + − e) 6 5 9
t t
+ − − f) 3 4 7 6
x x x
+ − + −
11. Simplify each of the following expressions by collecting like terms.
a) 5 6 ( 3 )
x x x
− + + − b) 8 ( 2 )
x x
− − − c) 16 4 12
x y x y
− + +
d) 4 9 15
a a
− + − + e) 4 3 9 6
x x
− − + f) 2 4 9 ( 11 )
m m
− + + −
12. Simplify each of the following expressions by collecting like terms and the evaluate for 3
x =
and 4
y = − .
a) 9 8 4 5
x y x y
+ − + b) 7 ( 4 ) 8 15
x x
− − − − + c) 9 4 7
y y
− − + −
13. To check if the expressions 11 5 13 6 and 4 12 9 22
x x x x
− + − − − + + are
equivalent, Nikola substituted 3 for x in each expression and evaluated. Since
both expressions worked out to the same value of 25, he concluded that the
expressions are equivalent. Is Nikola’s conclusion correct? Explain.
14. Identify each of the following pairs as like terms or unlike terms.
a) 5x and 2
3x b) 8x
− and
2
3
x c) 2
1
2
t
− and 2
1
3
t d) 2
3y and 3
2y
15. Simplify each of the following expressions by collecting like terms.
a) 2 2
4 2 3 15
x x x x
+ + + b) 2 2
14 5 3 2
x x x x
+ + − c) 2 2
3 4 8 7
y y y y
− + + −
d) ( )
2 2
20 4 4 5
x x x x
− + + − − e) 2 2
3 ( 5 ) 10
a a a a
− − − − + f) 2 2
4 ( 3 )
x x x x
− + + −

4. Adding and Subtracting Monomials (Collecting Like Terms)
16. Simplify each of the following expressions by collecting like terms and the evaluate for 2
x = −
and 3
y = .
a) 2 2
2 4 6 7
x x x x
− + + − b) 2 2
3 8 7 5 9 2
x x x x
+ − + − − c) 2 2 2 2
3 2 2 4
x y x y
+ − +
d) 2 2
4 9 8 5
y y y y
− + − − e) 2 2
8 3 12 7
y y y
+ − + − f) 2 2
3 4 7 8 6 7
x y x y y x
− + − + −
17. State whether the two expressions are equivalent or not equivalent.
a) 5 3 and 8
x x x
+ b) 6 4 and 2 8
x x x x
+ + c) 5 3 and 3 5
y y y y
− −
d) 5 3 and 3 5
m m m m
− + − e) 2 2
6 and 6
t t t t
+ + f) 2 2 2
10 and 4 3 5 7
c c c c c c
− + − +
18. Nina is confused about the meaning of the expressions 2x and 2
x .
a) Explain the meaning of each of these expressions.
b) Are there any values of x for which these two expressions are equal? Explain.
19. Xianna earns $17 per hour at her summer job. At the end of each month, she also receives a
$100 bonus. Her friend, Marcel, earns $15 per hour with a $200 monthly bonus.
a) Write an expression to represent the total amount that Xianna earns for a
month in which she works t hours.
b) Write an expression to represent the total amount that Marcel earns for a
month in which he works t hours.
c) Write a simplified expression to represent the combined earnings for Xianna and Marcel for
a month in which they both worked t hours.
20. Simplify each of the following expressions by collecting like terms.
a) 2 2 2
1 5 2
2 6 3
x x x
+ − b)
3 1 2 1
5 3 3 5
a b a b
+ + − c)
2 5 4
5
3 6 3
x x
+ − +
21. Explain why
1
2
x and
2
x
are equal and then simplify the expression
5
2 4
x
x
+ .
22. Explain why
2
3
x and
2
3
x
are equal and then simplify the expression
2 4
3 9
x x
− .

5. Adding and Subtracting Monomials (Collecting Like Terms)
23. Simplify each of the following expressions by collecting like terms.
a)
2 5 4
4 3 6 3
x y y x
+ − + b)
3
2
3 4
v
v − + − c)
2 3 3
2
7 8 2
m n m
n
+ − +
24. Determine a simplified expression for the
perimeter of the trapezoid shown on the right.
25. Simplify each of the following expressions by collecting like terms.
a) 7 4 8 9 10
x y z x y z
− + − + − b) 6 8 4 3
x xy x xy
− − + c) 5 4 5 3 6
a abc ab abc ab
− + − +
26. Simplify each of the following expressions by collecting like terms.
a) 2 2
2 3 7 3
x y xy xy x y
+ − + b) 2 2 2 2
6 4 2 3
xy x y xy x y
+ − −
c) 2 2 2 2 2 2 2
7 4 8 3 2
a b a b ab a b a b
− − + + − d) 2 2
6 6 10 2 4
xy x yx y xy
+ + + −
27. The width of a rectangle is x metres. The height of the rectangle is three times the width.
Determine a simplified expression to represent the perimeter of the rectangle.
28. A square has a side length of 5a cm. A triangle has a base of 4a cm and a height of 7a cm.
Determine a simplified expression to represent the difference in the areas of these two shapes.
Which shape has the greater area?
29. A circle has a radius that is twice the length of a smaller circle’s radius. If the radius of the larger
circle is r cm, determine a simplified expression to represent the exact difference in the areas of
the two circles.
3x
x
2y 4y

6. Adding and Subtracting Monomials (Collecting Like Terms)
CHECK YOUR UNDERSTANDING
1. a) 3 b) 4 c) 3 d) 5
2. a) 2, 3 b) 4, 3 c) 4, 9
3. a) like terms b) unlike terms c) like terms d) unlike terms
4. a) 8 b) 15 c) 4
− d) 1 e) 1
−
5. a) 4x b) 7y c) 8x d) 8a e) 0 f) 4k
− g) 3w
− h) z
−
6. a) 2 3
x y
+ b) 7 16
a b
+ c) 7 13
g h
+ d) 6 5
c d
+ e) 3x y
− + f) 4
m n
− +
7. Shagun’s claim is incorrect. 5x and 2 are not like terms and thus cannot be combined into a single
term.
8. Both Kalani and Marc were correct, since adding 7
− has the same effect as subtracting 7 (moving
left 7 on the number line).
9. a) 8 3
x − b) 4 6
x
− + c) 8 4
x y
− d) 9 4
a b
− +
10. a) 7 14
x + b) 11 5
x + c) 2 16
p
− + d) 3 4
y
− − e) 5 4
t − f) 4 11
x
− +
11. a) 2x
− b) 6x
− c) 17 8
x y
+ d) 3 6
a + e) 5 3
x
− + f) 15 11
m
− +
12. a) 5 13 ; 37
x y
+ − b) 3 7 ; 2
x
− + − c) 5 2 ; 18
y
− −
13. No. Nikola has only shown that the two expressions are equal when 3
x = . He has not shown
that the expressions are equal for all values of x. Simplifying the expressions by collecting like
terms gives 6 7
x + and 5 10
x + , which are not equivalent.
14. a) unlike terms b) like terms c) like terms d) unlike terms
15. a) 2
6 18
x x
+ b) 2
17 3
x x
+ c) 2
3 5
y y
− +
d) 2
24x x
− − e) 2
9 2
a a
+ f) 2
2 7
x x
−
16. a) 2
4 3 ; 22
x x
− b) 2
8 9 ; 25
x x
− − c) 2 2
6 ; 58
x y
+ d) 2
6 13 8 ; 23
y y
− + − −
e) 2
10 20 ; 67
y y
− + + − f) 2 2
3 2 8 ; 54
x y y
+ − −
17. a) equivalent b) equivalent c) not equivalent d) equivalent e) not equivalent
f) equivalent
ANSWERS

7. Adding and Subtracting Monomials (Collecting Like Terms)
18. a) 2x x x
= + , whereas 2
x x x
= × .
b) 0 and 2. When 0
x = , both expressions work out to 0. When 2
x = , both expressions work
out to 4.
19. a) 17 100
t + b) 15 200
t + c) 32 300
t +
20. a) 2
2
3
x b)
19 2
15 15
a b
+ c)
1 19
6 3
x
− +
21. Multiplying x by
1
2
is equivalent to dividing x by 2. Also,
1 1 1 1
2 2 2 1 2 1 2
x x x
x x
×
= × = × = =
×
.
The simplified expression is
7 7
or
4 4
x
x
 
 
 
.
22. Multiplying x by
2
3
is equivalent to multiplying x by 2 and then dividing the result by 3. Also,
2 2 2 2 2
3 3 3 1 3 1 3
x x x
x x
×
= × = × = =
×
. The simplified expression is
2 2
or
9 9
x
x
 
 
 
.
23. a)
19 1 19
or
12 6 12 6
x y
x y
 
− −
 
 
b)
2 5 2 5
or
3 4 3 4
v
v
 
+ +
 
 
c)
17 19 17 19
or
14 8 14 8
m n
m n
 
− + − +
 
 
24. 4 6
x y
+
25. a) 6 5 2
x y z
+ − b) 2 5
x xy
− c) 5 11 7
a ab abc
+ −
26. a) 2
5 4
x y xy
− b) 2 2
4xy x y
+ c) 2 2 2 2
9 8
a b a b ab
− − + d) 2 2
6 12 2
x xy y
+ +
27. 8 m
x
28. 2 2
11 cm
a ; the square has the greater area
29. 2 2
3
cm
4
r
π
ANSWERS