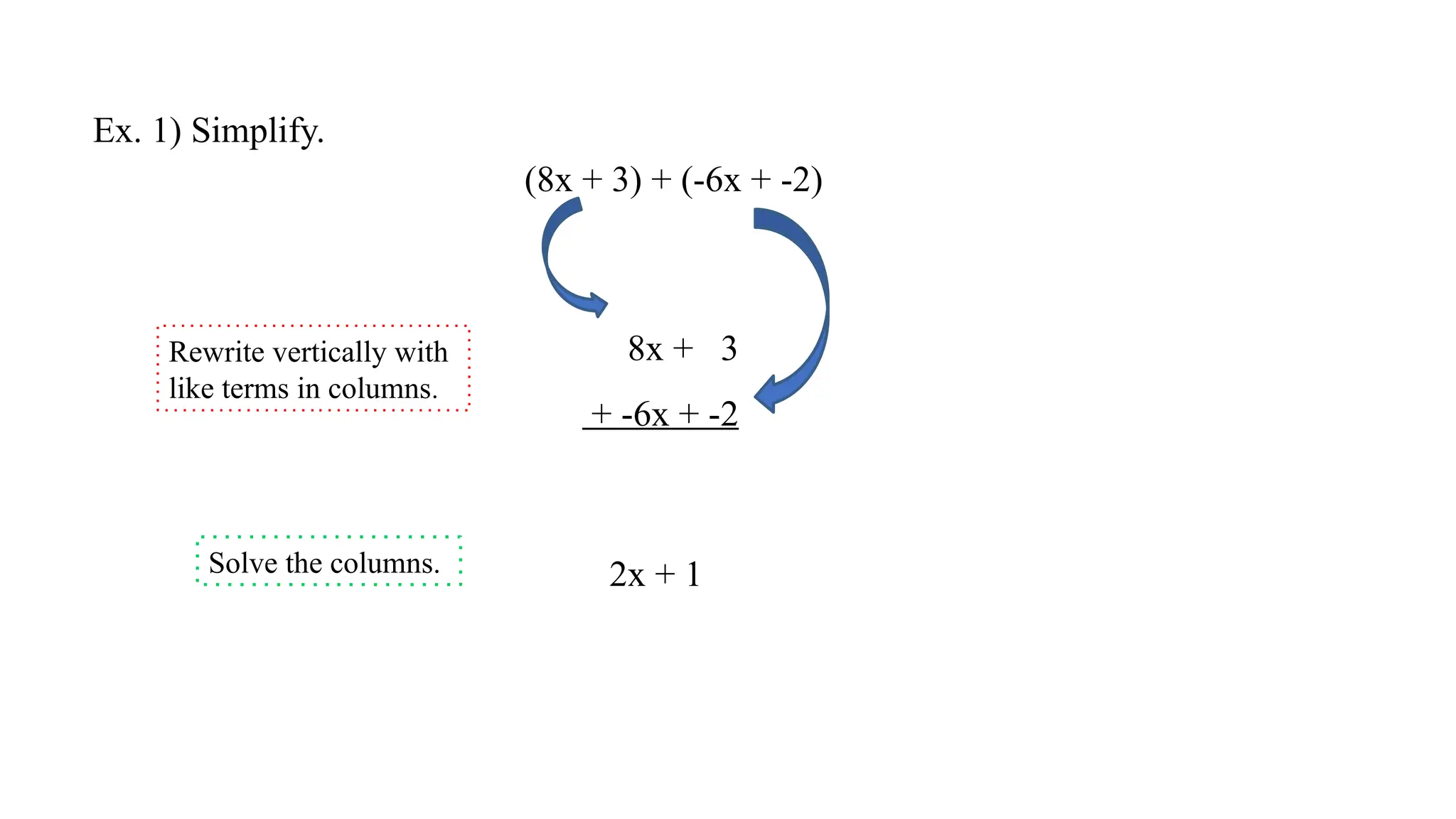
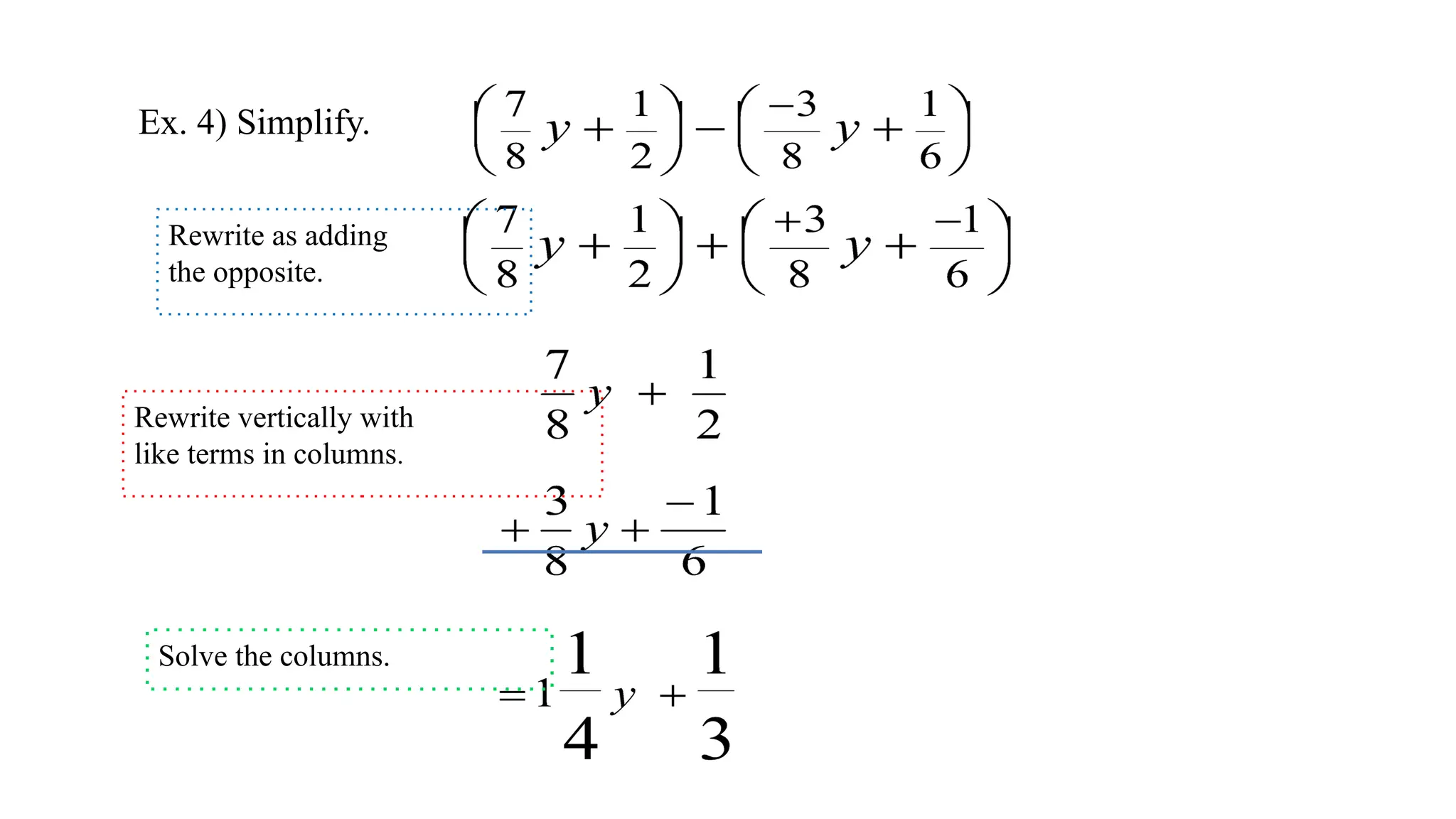The document explains how to add and subtract like terms in algebra, defining like terms as those with the same variables and exponents. It provides rules for both addition and subtraction, emphasizing the need to align like terms and the process of distributing negative signs. The document also includes examples for clarity and concludes with a recap of the distributive property and simplifying expressions.

1. Adding and
Subtracting Like
Terms

2. Like terms are terms that have the same
variables with the same exponents.
Like Terms
-3x, 8x, - x
6w2
, -12w2
, w2
Unlike Terms
20x, x2
, x3
6xy, 2xyz, w2
Combine Like Terms

3. RULES FOR ADDITION
• Put the two sets of expressions on top of each other
to add like terms
• Simplify

4. Ex. 1) Simplify.
Solve the columns.
(8x + 3) + (-6x + -2)
2x + 1
Rewrite vertically with
like terms in columns.
8x + 3
+ -6x + -2

5. Ex. 2) Simplify. (-5x – 9) + (6x + 1)
= x – 8
Rewrite vertically with
like terms in columns.
Solve the columns.
-5x – 9
+ 6x + 1

6. RULES FOR SUBTRACTION
• The subtraction sign in front of an expression in
parentheses means that you will have to “distribute”
the negative to everything inside.
• We can rewrite the problem:
– Change the minus sign to a plus sign
– Change all of the #s inside the parentheses to their
opposites

7. Ex. 1) Simplify. (8x + 3) – (6x + 2)
Rewrite as adding
the opposite.
Solve the columns.
(8x + 3) + (-6x + -2)
2x + 1
Rewrite vertically with
like terms in columns.
8x + 3
+ -6x + -2

8. Ex. 2) Simplify. (-6x + 1) – (2x – 5)
(-6x + 1) + (-2x + 5)
-8x + 6
Rewrite as adding
the opposite.
Rewrite vertically with
like terms in columns.
Solve the columns.
-6x + 1
+ -2x + 5

9. Ex. 3) Subtract (-2x + 5) from (-4x – 7).
(-4x – 7) + (+2x + -5)
-4x + -7
+ 2x + -5
= -2x – 12
(-4x – 7) – (-2x + 5)
Be careful with order as you
set up the subtraction problem!
Rewrite as adding
the opposite.
Rewrite vertically with
like terms in columns.
Solve the columns.

10. Ex. 4) Simplify.
Rewrite as adding
the opposite.
Rewrite vertically with
like terms in columns.
Solve the columns.

11. Combining Like Terms
1. Determine which terms are like terms.
2. Add or subtract the coefficients of the like
terms.
3. Multiply the number found in step 2 by the
common variable(s).
Example: 5a + 7a = 12a
RECAP

12. Distributive Property
For any real numbers a, b, and c,
a(b + c) = ab + bc
Example: 3(x + 5) = 3x + 15
(This is not equal to 18x! These are
not like terms.)

13. Simplifying an Expression
1. Use the distributive property to remove
any parentheses.
2. Combine like terms.
Example:
Simplify 3(x + y) + 2y
= 3x + 3y + 2y (Distributive Property)
= 3x + 5y (Combine Like Terms)
(Remember that 3x + 5y cannot be combined because
they are not like terms.)