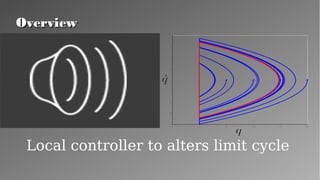
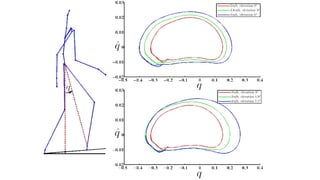
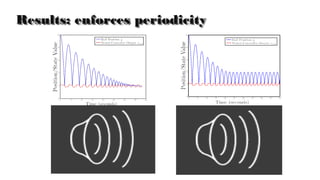
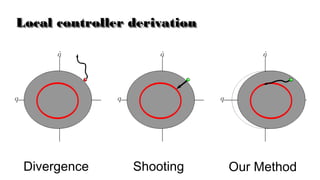
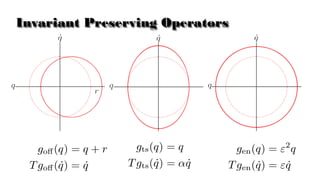
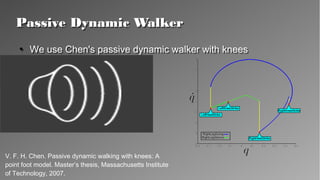
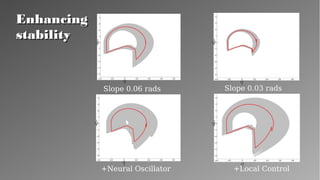
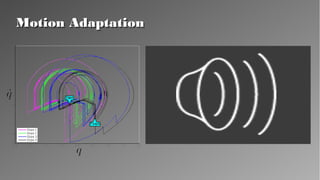
The document presents a theory for motion primitive adaptation, addressing issues in character animation and robotics, emphasizing the importance of energy-efficient, robust, and adaptable controllers. It discusses the role of motion primitives and the central nervous system in locomotion, proposing methods for enhancing stability and performance through local and global control strategies. The findings highlight the significance of preserving motor invariants and suggest potential applications in robotics and rehabilitation.

1. A Theory For
Motion Primitive
Adaptation
A Theory For
Motion Primitive
Adaptation
Richard Southern
National Centre for
Computer Animation
Richard Southern
National Centre for
Computer Animation
Liu, F.; Southern, R.; Guo, S.; Yang, X.; Zhang, J. J.; , "Motion
Adaptation With Motor Invariant Theory," Systems, Man, and
Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2013

2. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

3. Motivation: Character AnimationMotivation: Character Animation
●
Still lots of problems in game character animation
– Handling lots of character collisions (crowds)
– Repetition of pre-recorded animations
– Sliding when running into walls
●
Still lots of problems in game character animation
– Handling lots of character collisions (crowds)
– Repetition of pre-recorded animations
– Sliding when running into walls
The following clips thanks to David Greer @ NaturalMotion

7. Motivation: RoboticsMotivation: Robotics
“At present there is no accepted theory of how animals can, or
robots might, be energy-stingy, robust, versatile and adaptable.
Finding plausible schemes for the organization of a controller
that has these features is, I think, the key problem in
locomotion research today."
Andy Ruina, Cornell Robotics Group
“At present there is no accepted theory of how animals can, or
robots might, be energy-stingy, robust, versatile and adaptable.
Finding plausible schemes for the organization of a controller
that has these features is, I think, the key problem in
locomotion research today."
Andy Ruina, Cornell Robotics Group

9. Basic Assumptions of Low Level Motor ControlBasic Assumptions of Low Level Motor Control
●
Brain not used much in low level locomotion
●
Motion Primitives: building blocks of complex motion (e.g. frog
wave)
●
Body+Environment=Motion – animals don't move the way they
want, but the way they can (e.g. whale vs fish)
●
The central nervous system (CNS) only controls final motion
result, not process (equilibrium point hypothesis)
●
Brain not used much in low level locomotion
●
Motion Primitives: building blocks of complex motion (e.g. frog
wave)
●
Body+Environment=Motion – animals don't move the way they
want, but the way they can (e.g. whale vs fish)
●
The central nervous system (CNS) only controls final motion
result, not process (equilibrium point hypothesis)
M. Latash, Neurophysiological Basis of Movement. Champaign, IL: Human Kinetics Publ., 2008.
E. Bizzi, S. Giszter, E. Loeb, F. Mussa-Ivaldi, and P. Saltiel, “Modular organization of motor behavior in the frog’s spinal cord,” Trends
Neurosci.,vol. 18, no. 10, pp. 442–446, Oct. 1995.
A. G. Feldman, “Once more on the equilibrium-point hypothesis (λ model) for motor control,” J. Motor Behav., vol. 18(1), 17–54, Mar. 1986.

10. Basic Assumptions cont.Basic Assumptions cont.
●
All interesting motion is periodic
●
Motion adaptation: CNS “tweaks” these primitives to adapt
to environmental changes
●
We're going to describe “tweaking” mathematically
●
All interesting motion is periodic
●
Motion adaptation: CNS “tweaks” these primitives to adapt
to environmental changes
●
We're going to describe “tweaking” mathematically

11. What we don't do (yet)What we don't do (yet)
●
High level motion planning
– Computer vision
– Adaptation selection
●
Use complex biomechanical models (no ankles, muscles,
running)
●
Build robots
●
Rigorously test hypothesis on humans subjects
●
High level motion planning
– Computer vision
– Adaptation selection
●
Use complex biomechanical models (no ankles, muscles,
running)
●
Build robots
●
Rigorously test hypothesis on humans subjects

12. State (Dynamic) StabilityState (Dynamic) Stability
●
How well does it respond
to perturbations in state
space? (e.g. walker is
pushed)
●
Region of stability = basin
of attraction
●
How well does it respond
to perturbations in state
space? (e.g. walker is
pushed)
●
Region of stability = basin
of attraction

13. Structural StabilityStructural Stability
●
If we change the system (e.g. add a term to the function),
does the topology change?
●
If we change the system (e.g. add a term to the function),
does the topology change?

14. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

15. OverviewOverview

16. OverviewOverview
No input – not much happening

17. OverviewOverview
Global controller ensures
stable periodic system

18. OverviewOverview
Local controller to alters limit cycle

19. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

20. The Motor InvariantThe Motor Invariant
●
The motor invariant we want to preserve is the topology of
the dynamic system.
●
Type and Number of attractors do not change.
●
Shape of attractor and basin may change.
●
The motor invariant we want to preserve is the topology of
the dynamic system.
●
Type and Number of attractors do not change.
●
Shape of attractor and basin may change.

21. Theory of Valid Motion AdaptationTheory of Valid Motion Adaptation
●
For example: walker continues to walk, ball keeps bouncing
●
Evidence: motion capture analysis, handwriting
adaptation*
●
Realised through Lie group symmetry
●
For example: walker continues to walk, ball keeps bouncing
●
Evidence: motion capture analysis, handwriting
adaptation*
●
Realised through Lie group symmetry
*Affine differential geometry analysis of human arm movements
Tamar Flash and Amir A. Handzel, Biol Cybern. 2007 June; 96(6): 577–601.
A valid motion adaptation is one which
preserves the motor invariant

23. What does this mean?What does this mean?
●
These are validity conditions for motion adaptation
●
We can construct energy efficient controllers to make a
system more stable under certain environmental
conditions
●
These are validity conditions for motion adaptation
●
We can construct energy efficient controllers to make a
system more stable under certain environmental
conditions

24. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

25. Application 1: Global ControllerApplication 1: Global Controller
●
Design a controller to enhance state stability, or grow the
basin of attraction
●
Without changing the type or number of attractors
●
Design a controller to enhance state stability, or grow the
basin of attraction
●
Without changing the type or number of attractors

27. EntrainmentEntrainment
●
Couple an unconditionally stable
oscillator with a potentially unstable
one
●
Stable oscillator controls unstable one
●
Both oscillators assume same period
●
Strong biological evidence
●
Couple an unconditionally stable
oscillator with a potentially unstable
one
●
Stable oscillator controls unstable one
●
Both oscillators assume same period
●
Strong biological evidence
A. H. Cohen, “Evolution of the vertebrate central pattern generator for
locomotion,” in Neural Control of Rhythmic Movements in Vertebrates.
Hoboken, NJ: Wiley, 1988, pp. 129–166.

28. Oscillator couplingOscillator coupling
●
We use Matsuoka oscillator: exactly one periodic attractor.
●
F is mechanical system
●
S neural oscillator
●
Controller u input/output derived from oscillator
parameters / mechanical system parameters
●
h in/out user entrainment parameters
●
We use Matsuoka oscillator: exactly one periodic attractor.
●
F is mechanical system
●
S neural oscillator
●
Controller u input/output derived from oscillator
parameters / mechanical system parameters
●
h in/out user entrainment parameters
K. Matsuoka. Sustained oscillations generated by mutually
inhibiting neurons with adaptation. Biological
Cybernetics, 52(1):345–353, 1985.

29. Results: greater structural stabilityResults: greater structural stability

30. Results: enforces periodicityResults: enforces periodicity

31. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

32. Application 2: Local ControllerApplication 2: Local Controller
●
Reasons to transform the dynamic system:
– Move system so current state is within basin of attraction,
accounting for terrain variation
– Change frequency of system (walk faster, bounce ball faster)
– Change style of motion (more energetic, bounce ball higher)
●
Effectively realised as a local affine transform to the state
space.
●
Reasons to transform the dynamic system:
– Move system so current state is within basin of attraction,
accounting for terrain variation
– Change frequency of system (walk faster, bounce ball faster)
– Change style of motion (more energetic, bounce ball higher)
●
Effectively realised as a local affine transform to the state
space.

33. Local controller derivationLocal controller derivation
Divergence Shooting Our Method

34. Lie Group Control SymmetryLie Group Control Symmetry
●
Transforming a motion by a function g is equivalent
to transforming every state by g.
●
For each action g there is a corresponding “lift”
action Tg applied to tangential space
●
Control symmetry: solve Euler-Legrange equations
for transformed and untransformed systems
●
Transforming a motion by a function g is equivalent
to transforming every state by g.
●
For each action g there is a corresponding “lift”
action Tg applied to tangential space
●
Control symmetry: solve Euler-Legrange equations
for transformed and untransformed systems

35. Invariant Preserving OperatorsInvariant Preserving Operators

36. Controller DerivationController Derivation

37. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

38. Motion PrimitivesMotion Primitives
●
Difficult to decouple motion primitives from complex
motion
●
Walking triggers little brain activity, uses very little energy
●
Passive Dynamic Walker (with knees) from robotics
●
Mechanical, physics based model, not a muscle model
●
Difficult to decouple motion primitives from complex
motion
●
Walking triggers little brain activity, uses very little energy
●
Passive Dynamic Walker (with knees) from robotics
●
Mechanical, physics based model, not a muscle model
The following clip from the Cornell Robotics Group

40. Passive Dynamic WalkerPassive Dynamic Walker
●
We use Chen's passive dynamic walker with knees●
We use Chen's passive dynamic walker with knees
V. F. H. Chen. Passive dynamic walking with knees: A
point foot model. Master’s thesis, Massachusetts Institute
of Technology, 2007.

41. Enhancing
stability
Enhancing
stability
Slope 0.03 radsSlope 0.06 rads
+Neural Oscillator +Local Control

42. Motion AdaptationMotion Adaptation

43. Talk StructureTalk Structure
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results
●
Background
●
Overview
●
Theory for Motion Adaptation
●
Entrainment for Structural Stability
●
Local Controllers for State Stability
●
Walking model
●
Results

44. ResultsResults
●
Controller design choice influences state stability while
maintaining structure
●
Computationally trivial – a couple of matrix multiplications
at each time step
●
Very energy efficient – cost of transport 0.02 (half of
Cornell Ranger, tenth of a human)
●
Controller design choice influences state stability while
maintaining structure
●
Computationally trivial – a couple of matrix multiplications
at each time step
●
Very energy efficient – cost of transport 0.02 (half of
Cornell Ranger, tenth of a human)

45. ApplicationsApplications
●
Robot controller design
●
Rehabilitation: understanding human motion adaptation
●
One day: in character synthesis for games
●
Robot controller design
●
Rehabilitation: understanding human motion adaptation
●
One day: in character synthesis for games

46. ChallengesChallenges
●
Describing complex mechanical systems with solvable
dynamic models (ankles, running and muscles)
●
More complex (not affine transform) local controllers
●
Isolating motion primitives
●
Describing complex mechanical systems with solvable
dynamic models (ankles, running and muscles)
●
More complex (not affine transform) local controllers
●
Isolating motion primitives

47. Questions?Questions?

48. AppendicesAppendices

49. Why Periodic Motion?Why Periodic Motion?
Using Degallier and Ijspeert 2010 as a reference, we
argued that most motion is probably periodic, on a
biological level at least.
Of the three types of attractors, chaos is not applicable to
motion control problems, and fxed point attractors can
be easily modeled using a traditional proportional
derivative controller,which in many cases is a trivial
problem.
For these reasons, periodic motion is of most interest to
biology and robotics researchers, and are the most
difficult to explain.
Using Degallier and Ijspeert 2010 as a reference, we
argued that most motion is probably periodic, on a
biological level at least.
Of the three types of attractors, chaos is not applicable to
motion control problems, and fxed point attractors can
be easily modeled using a traditional proportional
derivative controller,which in many cases is a trivial
problem.
For these reasons, periodic motion is of most interest to
biology and robotics researchers, and are the most
difficult to explain.

50. Matsuoka OscillatorMatsuoka Oscillator

51. Chen's model for passive dynamic walking
with knees
Chen's model for passive dynamic walking
with knees

52. PD Controllers for Periodic MotionPD Controllers for Periodic Motion
●
Problems with methods from Van De Panne et al.:
– High gain (leading to stiffness)
– Reference trajectory
– Overshooting
●
Problems with methods from Van De Panne et al.:
– High gain (leading to stiffness)
– Reference trajectory
– Overshooting