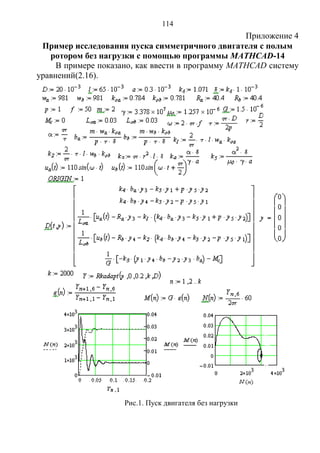
Монография посвящена моделированию нагрузочно-измерительных устройств с полыми немагнитными роторами, включая электромагнитные тормоза и асинхронные двигатели. Представлены математические модели, разработанные на основе теории электромагнитного поля, и примеры использования программного обеспечения Mathcad и COMSOL Multiphysics для анализа этих устройств. Работы предназначены для инженеров и студентов электротехнических специальностей, занимающихся разработкой и испытаниями электродвигателей.

![ББК 31.21
Потапов, Л. А. Моделирование нагрузочно-измерительных
устройств с полыми немагнитными роторами [Текст]+[Электронный
ресурс]: монография/ Л.А.Потапов, М.Л. Потапов, И.Л. Симонов. –
Брянск: БГТУ, 2010. – 116 с.
ISBN-978–5-89838-520-0
Представлены математические модели, разработанные на основе
теории электромагнитного поля, приведены примеры моделирования с
помощью программы MathCAD 14 и программного комплекса COM-
SOL Multiphysics 3.4 электромеханических устройств с полыми немаг-
нитными роторами (электромагнитные тормозы и демпферы, асин-
хронные двигатели, тахогенераторы и датчики угловых ускорений).
Рассмотрена их реализация в качестве нагрузочно-измерительных
устройств для испытания электродвигателей.
Монография предназначена для инженерно-технических работ-
ников, связанных с разработкой нагрузочно-измерительных устройств
для испытания двигателей и может быть использована студентами
электротехнических специальностей вузов при выполнении курсового
и дипломного проектов.
Ил.120. Библиогр. – 124 назв.
Научный редактор В.П. Маклаков
Рецензенты: кафедра «Энергетика и автоматизация производст-
венных процессов» Брянской государственной ин-
женерно- технологической академии;
кандидат технических наук Н. И. Ушев
Редактор издательства Л.Н. Мажугина
Компьютерный набор Н.А.Синицына
Темплан 2010 г.,48
Подписано в печать 19.10.10. Формат 60х84 1/16. Бумага офсетная. Офсетная
печать. Усл. печ.л. 6,74 Уч.-изд.л. 6,74 Тираж 500 экз. Заказ
Брянский государственный технический университет
241035, Брянск, бульвар им. 50-летия Октября,7, тел. 58-82-49
Лаборатория оперативной полиграфии БГТУ, ул. Институтская,16
ISBN 978–5-89838-520-0 © Брянский государственный
технический университет, 2010
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-2-320.jpg)


![5
ВВЕДЕНИЕ
Электромеханические устройства с полыми немагнитными рото-
рами могут быть выполнены в виде электромагнитных тормозов и
демпферов, асинхронных двигателей и тахогенераторов, датчиков уг-
ловых ускорений.
Наиболее широко применяются асинхронные двигатели. Для их
расчета при проектировании разработаны различные методы, осно-
ванные на теории электрических цепей, в которых используются клас-
сические Т- и Г-образные схемы замещения машины переменного то-
ка. Различаются они чаще всего способами расчета параметров полого
ротора.
На основе работ Е.М. Лопухиной, Г.С. Сомихиной и других ав-
торов был наиболее полно разработан параметрический метод расчета
асинхронных двигателей, тахогенераторов и датчиков момента. В этом
методе используются относительные величины, полученные делением
абсолютных параметров проектируемого устройства на активное со-
противление полого ротора. Для получения заданных свойств проек-
тируемого устройства эти относительные величины оптимизируют
определенными способами. При этом используются интегральные па-
раметры: токи, синусоидальные напряжения, потокосцепления. С их
помощью рассчитывают электромагнитные моменты и строят механи-
ческие характеристики М(п).
Расчету сопротивления полого ротора посвящено значительное
число работ [6, 12 – 15, 32, 36 – 38, 52 – 58, 103 – 113 и др.]. Сопро-
тивление полого ротора рассчитывают чаще всего исходя из предпо-
лагаемой картины распределения вихревых токов. Так, исходя из этой
картины рассчитывают сопротивления участков ротора, вдоль кото-
рых протекают эти токи. Предположение о распределении вихревых
токов по подобным прямоугольникам в своих работах принимают
Ю.М. Пульер, И.Я. Лехтман и частично Г. Мозер [103 – 113]. Если по-
ле вихревых токов ротора велико, Г. Мозер предлагает графо-
аналитический метод спиральных диаграмм [110] (исходя из распре-
деления вихревого тока по подобным прямоугольникам.
Используя теорию электромагнитного поля, Е.М. Лопухина по-
лучила [52] картину распределение вихревого тока в полом немагнит-
ном роторе без учета краевого эффекта. В работах [53, 54] было полу-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-5-320.jpg)
![6
чено выражение для активного сопротивления полого ротора, приве-
денного к числу фаз и витков обмотки статора.
В работах И.А. Вевюрко [12 – 15]. получена картина распределе-
ния вихревых токов с учетом вылетов ротора за сталь статора, а также
определено влияние массивного дна, соединяющего цилиндр с валом.
Конструктивное назначение дна такое, что оно всегда выполняется
толще стенок самого цилиндра ротора, поэтому рассматривается как
сверхпроводящая область. В работе [13] получены выражения для
анализа и расчета машины методом симметричных составляющих,
приводятся коэффициенты увеличения сопротивления полого ротора
для прямой и обратной последовательностей:
Показательна также работа Э. Хабигера [106]. В ней кроме до-
пущений, принятых в [12], принято допущение о распределении ин-
дукции магнитного поля вдоль длины машины по прямоугольному за-
кону. Затем вводятся две системы координат, одна из которых непо-
движна и связана со статором, другая – связана с ротором и, следова-
тельно, является подвижной. После этого устанавливается закон рас-
пределения магнитной индукции, определяется плотность тока ротора
и вращающий момент, а также выражения для электромеханической
постоянной времени и сопротивления полого ротора.
В более поздних работах [1–4,66] использовались способы расче-
та сопротивления полого ротора, аналогичные рассмотренным в рабо-
те [12]. Хотя основой этих способов является теория электромагнит-
ного поля, но в итоге в них используется схема замещения машины
переменного тока, полученной на основе теории электрических цепей.
Отличия их между собой заключается в принятых допущениях и спо-
собах определения параметров ротора.
С помощью интегральных параметров, в том числе и активного
сопротивления ротора, при значительно выраженном краевом эффек-
те невозможно учесть электромагнитные процессы, происходящие в
электромеханическом устройстве с полым немагнитным ротором
(ЭМУПНР). При изменении частоты вращения ротора его сопротив-
ление изменяется, что обычно не всегда учитывается. Вследствие это-
го значительно уменьшается точность расчета устройства, особенно
при анализе динамических режимов.
Еще один недостаток рассматриваемых способов расчета
ЭМУПНР заключается в том, что трудно установить влияние геомет-
рических размеров и других конструктивных факторов на значение
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-6-320.jpg)
![7
электромагнитного момента. Они определенным образом влияют на
сопротивление полого ротора, а тот в свою очередь на ток, и только
используя ток и напряжение, можно рассчитать значение электромаг-
нитного момента. Этот недостаток особенно проявляется при проек-
тировании испытательного оборудования, когда необходимо иметь
явные зависимости, связывающие параметры выходной (механиче-
ской) характеристики с геометрическими и электрическими парамет-
рами самого устройства.
Преимуществом получаемых на основе теории цепей выражений
для расчета сопротивления полого немагнитного ротора является их
наглядность и простота, однако, как показывают результаты экспери-
ментов, погрешности при использовании этих выражений иногда со-
ставляют сотни процентов [53, 54], что не оправдывает их простоты.
Кроме того, формулы для расчета сопротивления полого ротора не
позволяют определить реактивные параметры ротора, которые необ-
ходимы для расчета тахогенераторов, датчиков угловых ускорений и
датчиков момента. Причиной значительных погрешностей при таком
подходе к расчету сопротивления ротора является неопределенность
картины распределения вихревых токов.
Для электромагнитных тормозов, муфт и датчиков угловых уско-
рений, подключаемых под постоянное напряжение, указанные спосо-
бы расчетов параметров трудно применить. Для них разрабатываются
другие способы, в которых используются уравнения электромагнит-
ного поля и дифференциальные величины: плотность тока J, магнит-
ная индукция В, напряженность электрического поля Е. С помощью
этих величин рассчитывают электромагнитные моменты, механиче-
ские характеристики М(п). Таким же образом можно рассчитать
устройства переменного тока.
При проектировании нагрузочно-измерительных устройств
(НИУ) электромеханические устройства с полыми роторами
(ЭМУПНР) используются чаще всего в виде электромагнитных тормо-
зов или демпферов (например, в стыковочных устройствах космиче-
ских аппаратов) и значительно реже в виде муфт, датчиков скоростей
и угловых ускорений. При испытании тихоходных двигателей иногда
используют в качестве нагрузки асинхронную машину в режиме про-
тивовключения.
В настоящее время для расчета устройств с распределенными
вторичными средами разрабатываются комбинированные методы, со-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-7-320.jpg)
![8
гласно которым параметры проектируемого устройства рассчитыва-
ются по аналитическим зависимостям, а затем уточняется с помощью
конечноразностных или конечноэлементных моделей. Однако с по-
мощью 2D-конечноэлементных моделей невозможно учесть попереч-
ный краевой эффект, а разработка 3D-моделей затруднена из-за очень
высоких аппаратных требований к ЭВМ.
На основе многочисленных работ [10, 16 – 20, 43–44 и др.], по-
священных исследованию магнитогидродинамических машин, разра-
ботан метод расчета реального технического устройства. В соответ-
ствии с этим методом реальное техническое устройство заменяется
некоторой идеализированной схемой, для которой на основе теории
электромагнитного поля можно получить аналитические зависимости
для плотностей токов в роторе, магнитных индукций и электромаг-
нитного момента. Несмотря на существенное конструктивное отличие
магнитогидродинамических машин от классических электрических,
указанный метод расчета развит в более поздних работах [63–78, 82,
85 – 96 и др.] применительно к электромеханическому преобразовате-
лю с полым немагнитным ротором.
Применение современной вычислительной техники и программ-
ного обеспечения позволяет на основе уравнений теории электромаг-
нитного поля не только рассчитать электромагнитный момент рас-
сматриваемого устройства в установившемся режиме работы, но и
проанализировать распределение магнитных полей или токов в про-
странстве и во времени. При этом можно исключить допущения, при-
нятые в методах расчета электромеханических устройств, основанных
на теории электрических цепей. Именно таким образом получены и
исследованы с помощью аналитических и численных методов мате-
матические модели нагрузочно-измерительных устройств.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-8-320.jpg)

![10
вихревых токов в стали статора, явлением гистерезиса и насыщением
магнитной цепи пренебрегаем);
4. Магнитная индукция имеет только одну нормальную состав-
ляющую;
5. Несинусоидальные периодические величины представлены ря-
дом Фурье и анализируются для каждой гармоники в отдельности.
6. Еще одно допущение, упрощающее задачу расчета магнитного
поля и обеспечивающее выполнение четвертого допущения, заключа-
ется в замене обмотки статора, уложенной в специальные пазы и под-
ключенной под постоянное или многофазное переменное напряжение,
токовым слоем, имеющим одинаковую плотность по высоте воздуш-
ного зазора [17]. Плотность тока в этом слое определенным образом
связана с токами в обмотках статора и числом витков обмоток статора,
характеризующими распределение их в пространстве. Такая замена
используется многими авторами. Она имеет большое значение, так как
позволяет перейти от интегральных величин (ток в обмотке) к диффе-
ренциальным (плотность тока) и при необходимости обратно.
В результате упрощенная модель
электромагнитного тормоза может
быть представлена в виде двух полу-
пространств, заполненных ферромаг-
нитной средой с магнитной проницае-
мостью μ→, движущейся в зазоре
между ними со скорость v вдоль оси х
бесконечной немагнитной токопрово-
дящей полосы (рис.1). Силу торможе-
ния можно определить путем интегрирования произведения магнит-
ной индукции и плотности тока ротора по объему движущейся поло-
сы, ограниченному расстояниями: вдоль оси у – длиной ротора, вдоль
оси z расстоянием, равным зазору, вдоль оси х – расстоянием, равном
длине окружности ротора. Умножая эту силу на радиус ротора, опре-
деляют электромагнитный момент тормоза. Такая модель достаточно
широко применяется [17, 66, 85 – 96 и др.] и позволяет с учетом по-
правочных коэффициентов получать сравнительно хорошее совпаде-
ние с экспериментальными данными. В то же время она дает ясную
взаимосвязь параметров, переменных и выходных величин.
В этой модели зубчатый статор с обмоткой представлен в виде
бесконечной ферромагнитной полосы, имеющей относительную маг-
δ
J1 J2
z
x
vr
q
Рис. 1.1. Расчетная схема
АМПНР
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-10-320.jpg)
![11
нитную проницаемость μ→, при этом толщина полосы не имеет зна-
чения. В зазоре распределен токовый слой, имеющий одинаковую
плотность по высоте воздушного зазора [17]. Плотность тока в этом
слое определенным образом связана с токами в обмотках статора и
числом витков обмоток статора и изменяется вдоль оси x по гармони-
ческому закону. Плотность этого тока имеет только одну y-
составляющую
xJxI
p
wk
J m
об
sinsin 11 ,
где I
p
wk
J îá
m
1 ; p – число пар полюсов;
D
p2
; D – диаметр ро-
тора; w – число витков; kоб – обмоточный коэффициент; kç –
расчетный зазор, учитывающий зубчатость статора с помощью коэф-
фициента Картера kδ.
Плотность тока ротора уменьшается в δ/q раз (ротор заполняет
весь зазор), где q – толщина ротора, т.е. J2 = cJр,
q
c .
Используя известные уравнения
21 JJHrot ; ])[(2 BvgradcEcJ ;
][1
2
BvrotcJrotHHrotrot ; HB 0 ;
2
D
v ,
,,
,,,,
1
01101
0000
x
J
zJrotJyJ
x
B
vzBvrotvByBvBzBvxv
получим уравнение для магнитной индукции
x
J
x
BD
ñ
x
B
1
002
2
2
.
Переходя к комплексной форме записи и представляя
]Im[)( )(
11
xj
meJxJ
; Bxj
meBxB
Im ,
получим уравнение, устанавливающее зависимость магнитной индук-
ции от плотности тока статора:
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-11-320.jpg)
![12
100
2
2
JjB
D
сjB , тогда
)1(
10
j
Jj
B
, (1.1)
где ε – магнитное число Рейнольдса (МЧР).
p
DccD
42
2
00
. (1.1, а)
Электромагнитный момент выразим через уравнение элементар-
ной электромагнитной силы f = JB, которое после интегрирования по
объему воздушного зазора и умножения на радиус ротора примет вид
)1(2
]Re[
4
2 2
2
1
22
1
êý
êý
kJlD
BJkl
D
M . (1.2)
Исследуя полученное уравнение момента на максимум, определим
критическое значение МЧР εкр и максимальное значение момента:
εкр = 1,
2
2
1
2
max
JlD
M .
Тогда относительный момент определяется по выражению
1
2
1
2
2
maxM
M
m . (1.2, а)
Зная, что критическое
значение магнитного числа
Рейнольдса равно единице,
можно определить критиче-
ское значение угловой скоро-
сти ротора
2
00
42
cD
p
cD
êð
,
тогда относительная угловая
скорость Ω’=Ω/Ωкр= ε = ε’.
Таким образом, уравнение (1.2,а) представляет собой универсаль-
ную механическую характеристику m(ε)=m(Ω’) (рис. 1.2) любого элек-
тромагнитного тормоза с полым немагнитным ротором.
Это дает возможность, используя предполагаемые размеры тормо-
за, определить МЧР по зависимости (1.1,а) и по универсальной меха-
нической характеристике определить характер зависимости M(n). Если
ε<<1, то характер зависимости M(n) практически линейный, если ε→1,
m
1 2 ε, Ω
0,8
0,6
0,4
0,2
0 0,5 1,5 2,5
Рис.1.2. Универсальная механическая
характеристика
электромагнитного тормоза
к
3
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-12-320.jpg)
![13
то момент практически не зависит от скорости, если ε>1, то момент
убывает с увеличением скорости (что обычно нежелательно). Изменяя
величины, входящие в уравнение (1.1) можно подобрать оптимальный
характер механической характеристики тормоза.
1.2. Модель электромагнитного тормоза,
учитывающая краевые эффекты
Для учета влияния вылетов условно разобьем ротор на три обла-
сти (рис. 1.3): II – находится в рабочем зазоре между внутренним и
внешним статорами; III, IV – за пределами зазора. Плотности тока в
этих областях обозначим как J2, J3, J4, где J2 – плотность тока в рабо-
чем зазоре между статорами, а J3, J4 – плотности тока в областях вы-
летов ротора (с двух противоположных сторон).
Система уравнений Максвелла для рассматриваемых сред при
указанных условиях имеет вид [66]
;
;
;
0
21
ArotHB
Bv
t
A
gradE
EcJJHrot
(1.3)
J2
z
h2 h1
d2
J1
J4 J3
y
d1
δ
J1
vr
a
z
J2
x
Рис. 1.3. Расчетная схема электромеханического
устройства с полым немагнитным ротором
d1
y
x
II
III
IV
0
d2h2
h1
2πr
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-13-320.jpg)
![14
Здесь 21,,,, JJEHB – соответственно векторы магнитной индукции,
напряженности магнитного поля, напряженности электрического по-
ля, плотность тока статора, плотность тока ротора, v – вектор линей-
ной скорости движения среды относительно избранной системы коор-
динат. Плотность тока 1J будем считать заданной, а плотность тока
ротора 2J определяется электромагнитными процессами, происходя-
щими в машине.
Подставим второе уравнение системы (1.3) в первое уравнение
этой же системы. Тогда второе уравнение можно записать в виде
Bv
t
A
gradcJHrot 1 .
Возьмем операцию rot от левой и правой частей полученного вы-
ражения:
Bvrot
t
A
rotgradrotcJrotHrotrot 1 ,
так как HHrotrot 2
, 0 gradrot , BArot , то
][][ 011
2
Hvrot
t
H
cJrotBvcrot
t
B
cJrotH .
Таким образом, уравнение для напряженности магнитного поля
будет иметь вид
][01
2
Hvrot
t
H
cJrotH . (1.4)
Возьмем операцию rot от обеих частей второго уравнения систе-
мы (1.3):
Bvrot
t
B
Erot
. (1.5)
Учитывая, что напряженность электрического поля имеет только
составляющие Ex и Ey и пренебрегая эффектом вытеснения тока в ро-
торе, раскроем левую часть уравнения (1.5):
y
E
x
E
zErot xy
0 .
Согласно принятым допущениям, индукция магнитного поля
имеет только нормальную к поверхностям статоров и ротора состав-
ляющую. При развороте электрической машины на плоскости нор-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-14-320.jpg)







![22
Из этих уравнений следует, что 31 CCj ; 42 CCj ;
75 CCj ; 86 CCj ; 119 CCj ; 1210 CCj .
Из граничных условий
1111
6521
hhhh
eCeCeCeC
; (1.27)
1111
87243
hh
y÷àñò
hh
eCeCJeCeC
; (1.28)
2222
10921
hhhh
eCeCeCeC
; (1.29)
2222
1211243
hh
y÷àñò
hh
eCeCJeCeC
; (1.30)
011
87 dd
eCeC
; 022
1211 dd
eCeC
, (1.31)
следует что
12
78
d
eCC
; 22
1112
d
eCC
;
11111 2
7243
hdh
y÷àñò
hh
eeCJeCeC
;
22222 2
11243
hdh
y÷àñò
hh
eeCJeCeC
.
Так как 75 CCj , то 75 jCC ; 86 CCj , тогда
12
786
d
ejCjCC
,
С учетом уравнения (1.26), после преобразований получим [66]:
,
11
1
1Re
1
2
Re2
21
2
0
2
1
2
12
2
1
2
l
ecec
j
Blr
dyBJrM
ll
h
h
y
где ;0
ar
λ2
=α2
(1+jε); l = h1+h2;
;
1
1
;
11
1
;
11 4
3
5
36
5
2
36
65
1
l
e
c
c
c
cc
c
c
cc
cc
c
22
2
4
411
2
3
3
2
42
34
6 th;th;
11
11
hdchdce
cc
cc
c l
.
Для электромагнитного тормоза с симметричными вылетами ро-
тора, выполненного из одного материала (γ2 = γ3 = γ4 = γ), математиче-
ская модель в комплексной форме имеет более простой вид
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-22-320.jpg)
![23
h
h
y
xyyyxx
x
x
y
x
y
y
x
xx
x
x
y
y
y
dyBJrM
yJdyJhyJJJJ
y
J
Jj
y
J
Jj
y
J
J
y
J
JJ
a
rj
y
J
J
B
a
rJ
a
rj
y
J
JJBj
.Re2
;0ïðè0;ïðè0;ïðè;
;0;0;0
;0;0
;;
12
2
233232
3
3
2
22
3
2
3
2
2
3
2
3
2
202
2
2
2
2
1
2
202
2
2
2
2
11
Решая систему уравнений, получим:
;
thsh/ch
ch
12
0
1
3
2
hdhy
yB
J y
2
0
2
1
2
1
fBlr
M (1.31)
где
hdhh
jf
th/cth
1
11Re . (1.32)
При нормальном исполнении ЭМПНР влияние краевого эффекта
обычно невелико и вполне может быть учтено коэффициентом kк.э.
Сравнив уравнения (1.32) с уравнением (1.2) для тормоза с симмет-
ричными вылетами ротора получим:
hdhh
jfk ýê
th/cth
1
11Re. .(1.32, а)
Аналогично для электромагнитного тормоза с несимметричными
вылетами ротора [66]
l
ecec
jk
ll
ýê
11
11Re 21
. . (1.32, б)
Тогда электромагнитный момент тормоза можно определять по
уравнению
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-23-320.jpg)
![24
2
к.э
2
к.э
2
к.э
111
k
Wp
kBrpl
M
kIwkl
M 2
2
или,
4
0
2
1
2
00
,
где
rl
B
W 2
2 0
2
1 – энергия магнитного поля в рабочем зазоре
ЭМПНР.
1.4. Постоянная реакции и магнитное число Рейнольдса
Широко известный параметрический метод расчета [53–60] ис-
пользует безразмерные параметры, определяемые как отношение ре-
альных величин к сопротивлению полого ротора. В связи с тем, что
сопротивление полого ротора изменяется при изменении скорости
вращения, температуры его нагрева и, кроме того, определяется при-
ближенно, целесообразно применить иные способы расчета и иссле-
дования ЭМУПНР. Нами используется в качестве основной величины,
характеризующей интенсивность электромагнитных процессов в
ЭМУПНР магнитное число Рейнольдса (МЧР), которое также является
безразмерной величиной, но при этом связывает воедино скорость ро-
тора и другие конструктивные величины ЭМЧПНР. Через МЧР опре-
деляется другая константа – постоянная реакции Ср, устанавливающая
для каждого типа ЭМУПНР соотношение скорости ротора и основных
конструктивных параметров, при которых электромагнитный момент
достигает максимального значения.
В теории подобия широко используются безразмерные величины
(комплексы), которые получают смысл новых, характерных для рас-
сматриваемой задачи переменных. Наиболее значимые из них обозна-
чают по фамилиям выдающихся ученых – например, число Рейнольд-
са, число Прандтля и т.д. Эти величины (число Рейнольдса и т.д.) яв-
ляются критериями подобия и не являются константами, а изменяются
в широких пределах, характеризуя интенсивность процессов. В част-
ности число Рейнольдса
vL
Re в гидродинамике характеризует со-
отношение между силами инерции и силами трения в потоке жидко-
сти или газа. При этом ν – характерная для данной задачи скорость,
L– характерный линейный размер, χ – кинематическая вязкость жид-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-24-320.jpg)
![25
кости. При малых значениях числа Рейнольдса – течение жидкости
ламинарное, при больших значениях – турбулентное.
Число Рейнольдса можно также трактовать как отношение кон-
вективного переноса количества микродвижения жидкости к кондук-
тивному переносу количества микродвижения молекул (вязкое тре-
ние). Малым значениям числа Рейнольдса соответствуют медленные
течения вязких жидкостей, в уравнениях движения которых могут
быть исключены конвективные (нелинейные) члены. При больших
значениях числа Рейнольдса вблизи поверхности обтекаемых тел об-
разуется пограничный слой, вне которого движение жидкости может
рассматриваться как безвихревое, невязкое. Число Рейнольдса являет-
ся критерием подобия двух потоков вязкой жидкости, т.е. два одно-
типных течения вязкой жидкости могут быть динамически (по харак-
теру силового воздействия) подобны только тогда, когда у обоих тече-
ний равны числа Рейнольдса.
Для каждого вида течения существует критическое число Рей-
нольдса Reкр. Численное значение Reкр составляет несколько тысяч.
Так для вязкой жидкости, протекающей по длинной цилиндрической
трубе Reкр = 2300 [84].
В магнитной гидродинамике получают аналогичное число, опре-
делив отношение двух слагаемых в известном уравнении индукции
магнитного поля:
BBvrot
t
B
m
, (1.33)
где
4
2
c
m – магнитная вязкость, σ – электропроводность среды.
Магнитное число Рейнольдса определяют по формуле
m
m
vL
Re ,
аналогичной формуле из гидравлики. Однако сравнение МЧР прово-
дят по отношению к 1: Rem >> 1 или Rem << 1. При очень больших
значениях МЧР (Rem >> 1) можно пренебречь вторым слагаемым в
уравнении (1.33), представляющим собой диссипацию энергии вслед-
ствие протекания электрических токов. При этом проявляются усло-
вия «вмороженности» магнитных силовых линий в электропроводя-
щую среду, когда магнитный поток через заданную поверхность S,
ограниченную контуром, остается со временем постоянным.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-25-320.jpg)
![26
При очень малых значениях МЧР (Rem << 1) можно пренебречь
первым слагаемым в уравнении (1.33). Тогда окажется, что движение
электропроводящих жидкостей практически не влияют на магнитное
поле и другие электродинамические величины.
При исследовании электромеханических устройств с полыми не-
магнитными роторами (ЭМУПНР) также используют МЧР. Однако
смысл его и применение иное. Это число появляется автоматически
при решении уравнений идеализированных ЭМУПНР и его можно ис-
пользовать как критерий подобия. Однако физический смысл этого
числа применительно к электромеханическим устройствам с полыми
немагнитными роторами отличается от того, который имело число
Рейнольдса в гидродинамике (так как нет никаких течений, ни лами-
нарных, ни турбулентных).
Для электромагнитного тор-
моза, подключенного под посто-
янное напряжение, отсутствует по-
ток энергии со стороны статора в
ротор, поэтому определять МЧР
как отношение характерного раз-
мера к квадрату эквивалентной
глубины проникновения электро-
магнитной волны в движущуюся
среду [18] не очень оправдано. Бо-
лее оправдано определение МЧР
через отношение магнитных индукций [68], т.е.
B
B2
(1.34)
Это следует из уравнения (1.1) после некоторого преобразования
212
1010
2
10
)1(
)1(
)1(
)(
BB
JjJjJj
B
. (1.35)
Первая форма записи уравнения (1.35) позволяет построить кру-
говую диаграмму для суммарной магнитной индукции B (рис. 1.4), а
вторая и третья формы раскрывают фазовые соотношения между со-
ставляющими магнитной индукции B1 и B2. При изменении магнитно-
го числа Рейнольдса векторы В1 и В2 перемещаются по дуге окружно-
сти. Из диаграммы видно, что увеличение ε приводит к увеличению B2
и уменьшению B. При ε = 1, B2 = B и B отстает от B1 на 45о
. Численное
ε = ∞
1B
2BB
φВ
ε =1
1J
ε = 0
Рис. 1.4. Круговая диаграмма для
магнитной индукции в зазоре
электромагнитного тормоза
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-26-320.jpg)
![27
моделирование тормоза
[69] с учетом зубчато-
сти статора (рис. 1.5)
подтверждают, что при
ε = 1 суммарная маг-
нитная индукция
уменьшилась в 2 раз
и оказалась сдвинута в
пространстве на 45о
.
Картина магнит-
ных силовых линий
электромагнитного
тормоза, представлен-
ная на рис. 1.6 для двух режимов: ε =0 и ε =1, также подтверждает
сдвиг суммарного магнитного поля в пространстве на 45о
.
Определив электромагнитный момент бесконечно длинного тор-
моза на единицу длины в виде зависимости
)1(2 2
2
10
2
JD
M
и исследовав эту зависимость на максимум [68], установили, что при
εкр = 1 электромагнитный момент достигает максимального значения.
Таким образом, применительно к идеализированным (бесконечно
длинным) электромеханическим устройствам с полыми немагнитными
Рис. 1.6. Картина магнитных силовых линий тормоза:
а – при ε = 0, б– при ε = 1
а) б)
1
2
Bn, Тл
l, м
Рис.1.5. Распределение магнитной индукции
в зазоре тормоза: 1 – при ε =0, 2 – при ε=1
0,3
0
0
0,2
0,1
–0,1
–0,2
–0,3
–0,4
0,02 0,04 0,06 0,08 0,1
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-27-320.jpg)

![29
тельно, максимальное значение электромагнитного момента будет
сложным образом связано с этим числом. Применяя эти уравнения для
типовых конструкций тормозов, имеющих различные диаметры, но
сохраняющих соотношения l/τ > 2; Kв = 1,1…1,2, установили, что
максимум электромагнитного момента получается при ε = 1,2 ± 0,03,
т.е. соотношение
à0
оказывается постоянной величиной для
различных значений параметров, входящих в это уравнение. Это поз-
воляет определять эту величину, как некоторую константу Ср, учиты-
вающую влияние краевых эффектов для геометрически подобных
конструкций. Она не может определяться как магнитное число Рей-
нольдса через отношение характерного размера к квадрату эквива-
лентной глубины проникновения плоской электромагнитной волны в
движущуюся среду [18], а также через отношение магнитной индук-
ций [66].
Эта константа имеет иной смысл, ее можно назвать постоянной
реакции Ср, которая учитывает влияние краевых эффектов и устанав-
ливает для геометрически подобных конструкций связь между кон-
структивными параметрами и критической скоростью вращения, при
которой электромагнитный момент достигает максимального значения
кр
p
va
C
0
. (1.36)
Постоянная реакции Ср практически не изменяется для геомет-
рически подобных устройств одного типа при значительном измене-
нии их параметров. Для различных конструктивных исполнений элек-
тромеханических устройств с полыми немагнитными роторами она
может иметь различные значения. В частности, для типовых кон-
струкций тормозов и датчиков угловых ускорений Ср =1,2, а для элек-
тродвигателей и тахогенераторов Ср = 2,5…3 [78]. Это позволяет ис-
пользовать ее на начальном этапе проектирования для оценки формы
механической характеристики или для выбора конструктивных пара-
метров для заданных режимов работы. Так, при проектировании элек-
тромагнитного тормоза стремятся использовать практически линей-
ный участок механической характеристики от 0 до 0,7 Ср. Этому
участку соответствует изменение МЧР от 0 до 0,84 и скорости враще-
ния от 0 до
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-29-320.jpg)


![34
чены соответствующие формулы применительно к цилиндрическому
[96], дисковому [64] и коническому [89, 92, 93] роторам.
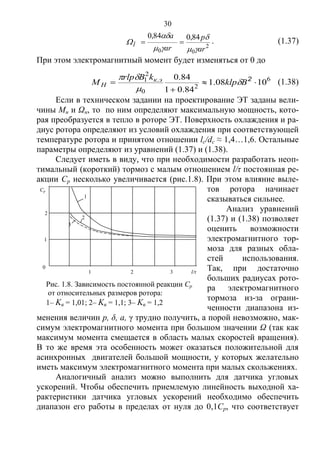
Одним из способов увеличения электромагнитного момента
ЭМУПНР является применение полых роторов с продольными проре-
зями, которые уменьшают растекание токов в поперечном направле-
нии. Многие авторы исследовали такие ЭМУПНР [1-4, 64, 91].
В работе [4] исследовались рациональные соотношения между
размерами в перфорированном полом роторе асинхронной микрома-
шины. Были установлены оптимальные соотношения между длиной
вылета гильзы ротора и длиной окон, а также определены длины окон
в материале ротора. Показано, что число окон целесообразно выби-
рать достаточно близким к числу зубцов статора, а ширину окна – ми-
нимально возможной.
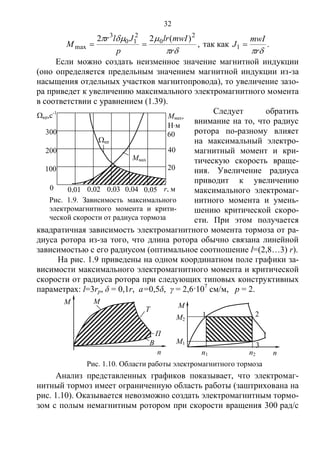
Подобный подход был применен
рядом авторов [85–96] при исследовании
электромагнитных демпферов.
В работе [86, 91] исследовались
электромагнитные демпферы с продоль-
ными прорезями (рис 1.11). Для плотно-
стей токов в активной зоне были полу-
чены на основе теории электромагнит-
ного поля следующие уравнения:
)sin(
)ch(
)sh(
1
10 xb
a
ó
CHJ k
k
k
kk
k
j
j
x
;
xj
k
k
k
kk
k
у ejxb
a
у
C
j
j
HJ
)cos(
)ch(
)ch(
1 1
0 .
Используя эти уравнения, определили тормозной момент
a
a
BC
j
Rе
ab
aR
H
M
k
k
kkk
k
)th(12
1
2
2
2 1
2
2
00
,
где а – длина паза, lb – вылет ротора за паз, b – расстояние между па-
зами, R – радиус ротора,
Рис. 1.11. Расчетная схема
демпфера с продольными
прорезями ротора
x
x
ylb
2a
b
l
∆
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-34-320.jpg)
![35
aajj
b
k
kkkkk /,),1(, 22222
, ajkk 22
,
)()(
)(
1 Bkkkk
b
k
lcthath
lcth
C
.
1при
2
1
2
1
1при
1
)1(1
2
k
abj
k
k
jabk
k
e
jab
e
A
1при
2
1при
)1(
)]cos()1(1[1
2
k
k
k
k
k
k
jk
ab
ab
B
При этом магнитное число Рейнольдса определялось по уравнению
dk2
0
,
где , – угловая скорость вращения, kd – коэффициент при-
ведения, учитывающий влияние пазов и насыщения. Полученные
уравнения позволили установить, что выполнение демпферов с акси-
альными прорезями на роторе увеличивает электромагнитный момент.
При увеличении числа прорезей максимальный электромагнитный
момент тормоза увеличивается и смещается в сторону малых частот.
1.7. Переходные режимы работы электромагнитного тормоза
Непосредственное решение полученных систем дифференциаль-
ных уравнений (1.24), содержащих частные производные, затрудни-
тельно, поэтому преобразуем эти системы к виду, удобному для их
решения с помощью ЭВМ. После преобразований эти системы долж-
ны содержать только обыкновенные дифференциальные уравнения,
разрешенные относительно производной и дополненные начальными
условиями.
В электромагнитном тормозе с полым немагнитным ротором ис-
пользуется только одна обмотка возбуждения, поэтому выражение для
плотности тока статора будет иметь вид
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-35-320.jpg)
![36
xbiJ a sin1
или в комплексной форме
xj
meJJ
11 , (1.40)
где a
oaa
am i
p
kw
biJ
2
1 .
В общем случае при исследовании переходных режимов демпфе-
ров и некоторых типов тормозов ток следует определять из уравнения
a
aa
aaa u
dt
d
dt
di
LiR
. (1.41)
В этом уравнении изменение потокосцепления и, следователь-
но, тока вызвано изменением тока в роторе при изменении скорости
вращения. При этом индукцию магнитного поля можно определить
следующим образом:
xtBxtBB bmam sincos , (1.42)
или в комплексной форме
ba BjBB . (1.43)
Определим потокосцепление обмотки
2
1
2
2
2
2
2
sincos
x
x
aoaa
boaaaoaaaa
lBkw
xdxlBkwxdxlBkwlBdxw
.(1.44)
Подставим комплексы первичной плотности тока (1.40) и индук-
ции магнитного поля (1.43) в уравнение (1.1) [66]:
1000
2
JjBr
a
j
t
Ba
B
. (1.45)
Выразим производную от индукции магнитного поля по времени:
jp
a
BJ
a
j
t
B
0
2
1
.
Левую и правую части уравнения (1.45) с учетом (1.43) можно
записать таким образом:
babaaa
ba
BjBjp
a
BjBib
a
j
t
BjB
0
2
.
Разложим полученное уравнение на две составляющие по осям,
сдвинутым на угол 90о
:
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-36-320.jpg)


![39
определить, как изменяется электромагнитный момент и магнитная
индукция в воздушном зазоре тормоза при подключении его под по-
стоянное напряжение (при неизменной скорости вращения), была за-
дана (рис. 1.12) угловая скорость Ω = 1000 с-1
, а в системе дифферен-
циальных уравнений отмечено, что ускорение равно нулю.
Результаты вычислений, полученные с помощью программы
Rkadapt, тут же выводятся в виде графических зависимостей от ис-
пользуемых в программе переменных или от вновь вводимых. В про-
грамме Rkadapt приняты обозначения: Y(1)
– время, Y(2)
– магнитная
индукция Ва, Y(3)1
– магнитная индукция Вb, Y(4)
– ток в обмотке воз-
буждения, Y(5)
–угловая скорость вращения.
В некоторых случаях необходимо определить, как протекают пе-
реходные процессы при мгновенном разгоне ротора, возбужденного
тормоза. Близкий к этому режим наблюдается, например, при работе
малоинерционных демпферов с полым ротором в амортизаторах сты-
ковочных механизмов космических аппаратов. В работе И.Х.
Хайрулина и Ф.Р. Исмагилова [94] получено аналитическое решение
для электромагнитного момента в переходном режиме в виде доволь-
но сложной зависимости, позволяющей, тем не менее, исследовать
влияние различных параметров на ударный момент (наибольшего от-
носительного момента). Гораздо быстрее и проще провести подобное
исследование, используя возможности моделирования этих режимов в
программе MathCAD.
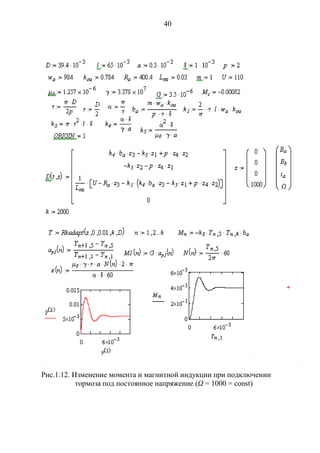
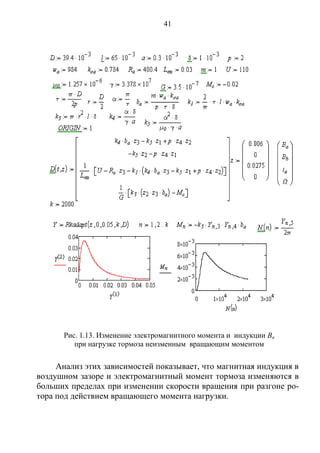
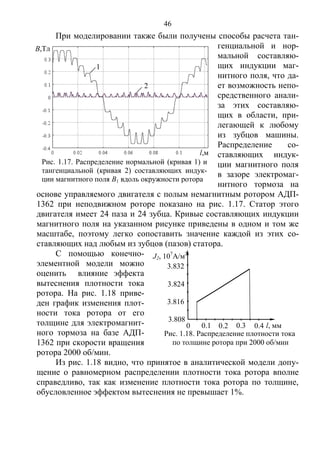
Чтобы определить, как изменяется электромагнитный момент и
магнитная индукция в воздушном зазоре тормоза при нагружении
предварительно возбужденного тормоза неизменным вращающим
моментом, были заданы (рис. 1.13) значения тока в обмотке возбужде-
ния и магнитная индукция в воздушном зазоре. Полученные резуль-
таты вычислений выведены в виде графических зависимостей.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-39-320.jpg)





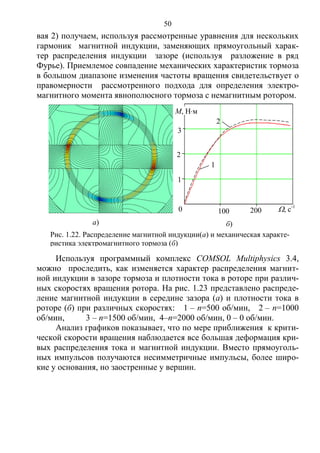
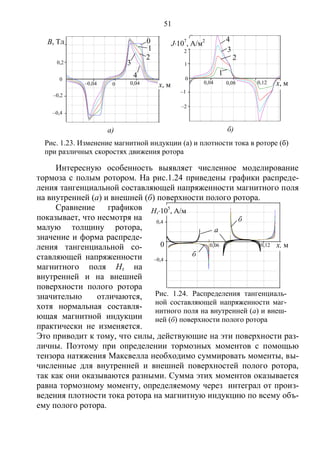




![56
][2 Bv
t
A
gradcEcJ ;
][1
2
Bvrotc
t
B
cJrotHHrotrot
.
Решая аналитически эти уравнения, получим уравнение для маг-
нитной индукции
x
J
x
B
ñv
t
B
ñ
x
B
1
0002
2
.
Представляя плотность тока статора и магнитную индукцию в
комплексной форме
]Im[),(
)
2
(
11
xtj
ebIxtJ , IjbJ 1 ,
]Im[),(
)(
B
xtj
BextB
, B
j
BeB
,
а также учитывая уравнения (1.1) и (2.8), получим уравнение, устанав-
ливающее зависимость магнитной индукции от плотности тока стато-
ра:
1000
2
JjBñvjBñjB ,
или
)1(
10
j
Jj
B
, (2.17)
где 2
2
0
2
0
2
0
4
)(
p
scDsc
v
c
– (2.18)
– магнитное число Рейнольдса,
r
p
c
, ,
v =
2
D
, pv ,
p
s
– скольжение.
Магнитное число Рейнольдса (МЧР) асинхронного двигателя за-
висит не только от угловой скорости ротора Ω (как для электромаг-
нитного тормоза), но и от круговой частоты вращения поля, т.е. оно
учитывает угловую скорость ротора относительно скорости вращения
поля.
Изменение тока статора определяется уравнением напряжений
)sin( utU
dt
d
dt
di
LiR
, при этом потокосцепление обмотки
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-56-320.jpg)
![57
)cos(
2
)sin(
2/
2/
B
m
Bma t
wlB
dxxtwlB
и )sin(
2
B
ma
t
lBw
dt
d
.
Так как BBB ttt sincoscossin)sin( ,
1
Btg ,
2
1
1
sin
B ,
2
1
cos
B , то
)cossin(
1
)cossin(
)1(
)(4
2
Ã
22
2
00
tt
IX
tt
p
Iwkl
dt
d mm
,
где
p
lwk
X 2
2
00
Ã
)(4
– главное индуктивное сопротивление фазной
обмотки.
Таким образом, уравнение напряжения будет иметь вид
)sin(cos
1
sin
1
cossin 2
Ã
2
Ã
Um
mm
mm tUt
IX
t
IX
tILtRI
.
Уравнение напряжения в комплексной форме для действующих
значений имеет вид
U
X
jXjXRI
2
Ã
Ã2
11
.
Умножая на сопряженный комплекс тока, получим:
jQPIUPI
X
XjRI
ÝÌ
2
2
Ã2
)
1
(
,
где 2
2
Ã
ÝÌ
1
IX
P – электромагнитная мощность.
Определим выражение для электромагнитного момента
])()([ 2
ï
2
ïÃ
ï
2
xxrrX
krnpUknP
M êýêýÝÌ
, (2.19)
где n – число фаз;
ÃX
R
r ; 2
1
Ï
r ;
ÃX
X
x σ
σ ; 2Ï
1
1
x ,
kкэ – коэффициент, учитывающий влияние краевых эффектов. Этот
коэффициент можно определять по уравнению (1.32, а, б).
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-57-320.jpg)
![58
Исследовав уравнение (2.19) на максимум, определим критиче-
ское значение МЧР и максимальный электромагнитный момент
22
12
1
xr
x
êð
; (2.20)
])()([ 2
ï.ê
2
ï.êÃ
ï.ê
2
xxrrX
rnpU
Mmax
, (2.21)
где 2ï.ê
1 êð
êð
r
; 2ï.ê
1
1
êð
x
.
Из уравнения (2.20) видно, что когда обмотки статора подключе-
ны под переменное напряжение, критическое значение МЧР всегда
больше 1.
Критическое значение МЧР для двигателя оказалось зависящим от
относительных значений сопротивления и индуктивности рассеяния
обмотки статора. Однако для типовых значений r и xσ МЧР изменяется
в небольшом диапазоне εкр=2…3. При этом активное сопротивление
оказывает большее влияние на смещение максимума электромагнит-
ного момента (рис.2.1) – при увеличении r критическое значение МЧР
стремится к 1
Скольжение связано с магнитным числом Рейнольдса уравнением
(2.18), ks . Критическое значение скольжения определяется кри-
тическим значением МЧР:
1.4
1.6
1.8
2.0
2.2
2.4
2.6
2.8
0 0.2 0.4 0.6 0.8 1 r
εкр
Рис. 2.1. Зависимость критического значения МЧР от относительных значений r и xσ:
1 – xσ=0.5; 2 – xσ=0.6; 3 – xσ=0.8
3
2
1
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-58-320.jpg)
![59
kp
kpkp
kp k
ñD
p
ñ
s
2
0
2
0
2
4
, (2.22)
где
ñD
p
ñ
k 2
0
2
0
2
4
.
Для большинства микродвигателей sкр>>εкр, т.е. максимум мо-
мента симметричного микродвигателя с полым немагнитным ротором
смещен в область скольжений значительно больших 1 и в рабочей об-
ласти при 0< s <1 зависимость M(s) может быть практически линей-
ной.
Из уравнения (2.22) следует, что относительное скольжение рав-
но относительному значению МЧР:
êðêðs
s
s
'' .
Так как в уравнениях (2.19) и (2.21) электромагнитный момент
определяется через МЧР, то целесообразно выразить относительный
момент
])()[(
])()[(
2
п
2
п.п
2
.п
2
.пп
xxrrr
xxrrr
M
M
m
кр
кркр
max
(2.23)
через относительное значение МЧР ε и, следовательно, относительное
скольжение
крs
s
s ' :
2
2
2
2п.
2
.п
2
.п2
)'(1
1
)'(1
'
)()(
)'(1
'
'
кркр
кр
кр
кркр
кр
кр
max
s
x
s
s
rr
xxrr
s
s
M
M
sm
(2.24)
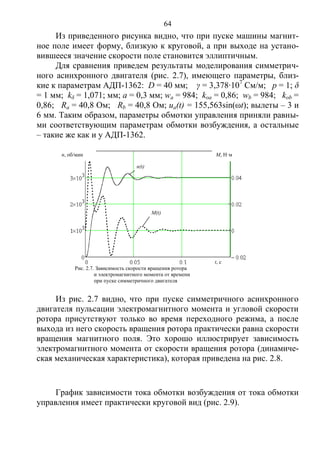
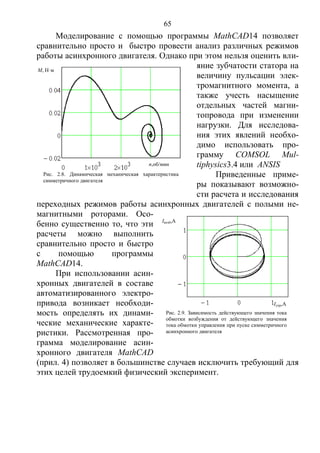
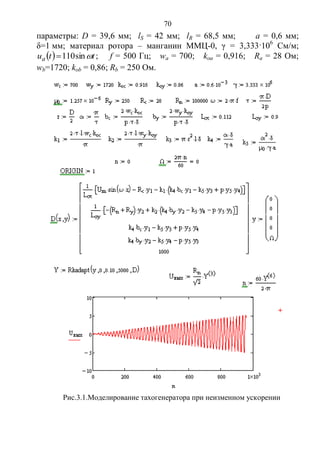
Анализ зависимости m(s’) показывает (рис. 2.2), что вид механи-
ческой характеристики симметричного асинхронного двигателя с по-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-59-320.jpg)


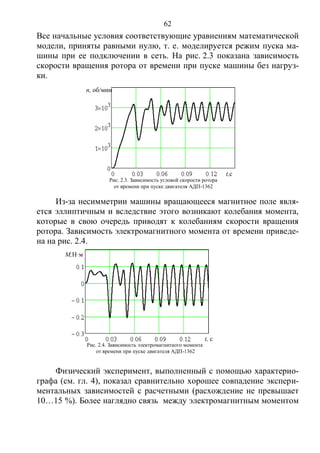
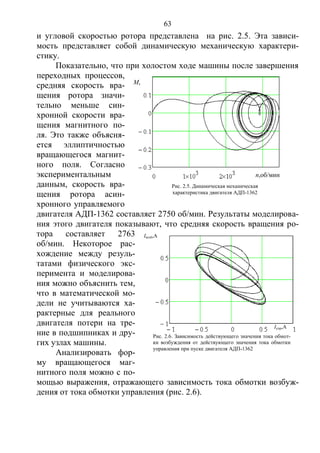




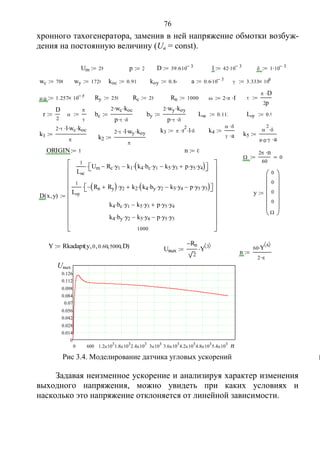
![71
Отметим, что при увеличении скорости вращения отклонение от
линейной зависимости у выходного напряжения тахогенератора зна-
чительно увеличивается и с некоторой скорости вращения выходное
напряжение начинает уменьшаться при дальнейшем увеличении ско-
рости вращения. На рис 3.2 приведены результаты моделирования то-
го же асинхронного тахогенератора АТ-231. Для получения более
высоких скоростей в рассмотренной модели (рис.3.1) изменено значе-
ние ускорения (число в пятой строке). На графике видно, что начиная
со скорости 25 000 об/мин, дальнейшее увеличении скорости приво-
дит к уменьшению выходного напряжения.
Для определения выходного напряжения тахогенератора разны-
ми авторами получены аналитические зависимости, например [101]
Uг = –j kUвv/(A-Bv2
)
В этой формуле коэффициенты А и В являются комплексными вели-
чинами, определяемыми через сопротивления прямой и обратной по-
следовательностей соответствующих схем замещения тахогенератора.
Определение этих коэффициентов является достаточно сложной и
трудоемкой задачей. Кроме того, представленная формула при значи-
тельном изменении скорости вращения неправильно отражает харак-
тер изменения выходного напряжения. Значительно проще и быстрее
Uвых, В
n, об/мин
Рис 3.2. График выходного напряжения тахогенератора при
высоких скоростях вращения
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-71-320.jpg)
![72
можно получить результат и провести исследование влияния кон-
структивных факторов на выходное напряжение тахогенератора с по-
мощью уравнений (3.3) и программы MathCAD (рис.3.1)
3.3. Устройство и принцип действия
датчика угловых ускорений
В последние годы стали чаще применяться датчики угловых ускоре-
ний с полыми немагнитными роторами в связи с разработкой различных
точных электроприводов. Известные методы получения угловых ускоре-
ний дифференцированием цифрового сигнала частотного таходатчика
(цифровые энкодеры, фотоэлектрические таходатчики и др.) приводят к
запаздыванию информации и значительному увеличению помех при
дифференцировании. Если помехи еще можно устранить с помощью раз-
личных низкочастотных фильтров, то устранить запаздывание информа-
ции о значении углового ускорения практически невозможно. Это запаз-
дывание определяется временем обработки частотного сигнала (преобра-
зованием частоты в угловую скорость и последующего дифференцирова-
ния). Так как в современных электроприводах датчик углового ускорения
устанавливается в цепи обратной связи, то для него недопустимо запаз-
дывание и, следовательно, неприемлем рассмотренный способ измерения
углового ускорения. Необходимы датчики реального времени, непосред-
ственно преобразующие угловое ускорение в электрический сигнал. Этим
требованиям вполне соответствуют датчики угловых ускорений с полыми
немагнитными роторами. В зарубежной литературе их часто называют
датчиками Феррариса (Ferraris sensor), усматривая некоторую аналогию
их принципа действия с процессами в известном диске Феррариса.
Получены десятки патентов различных датчиков ускорений (Ferra-
ris sensor) с полыми, дисковыми и линейными роторами [123 – 133], ис-
пользующих аналогию с диском Феррариса. Серийно выпускаются про-
мышленные образцы датчиков угловых и линейных ускорений. На рис.
3.3 представлен один из таких датчиков АСС-70, выпускаемых немецкой
фирмой Baumer Hubner CmbH. В конструкции предусмотрено крепле-
ние ротора датчика непосредственно на вал приводного двигателя. Статор
датчика имеет фланец, с помощью которого он крепится на статоре двига-
теля. Аналогичную конструкцию имеют датчики АСС-74, АСС-93 и
АСС-94. Выпускаются датчики различных модификаций, среди них име-
ются датчики с внутренним усилителем сигнала.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-72-320.jpg)

![74
Ф = с2п.
Изменяясь во времени при изменении скорости вращения, поток
Ф наводит в выходной обмотке ЭДС, пропорциональную ускорению:
dt
dn
c
dt
dÔ
weâûõ 3 , (3.4)
где с3 = –wc2 – коэффициент пропорциональности между ЭДС и угло-
вым ускорением dn/dt.
В реальной машине и датчике угловых ускорений зависи-
мость поперечного потока Ф от скорости вращения не является
строго линейной, а следовательно, выходная ЭДС не пропорцио-
нальна ускорению, т. е. коэффициент с3 в формуле (3.4) зависит от
скорости.
Уравнение выходной характеристики датчика ускорения получе-
но на основе решения дифференциальных уравнений в работах С.
Т. Казаряна [35]:
dt
dn
U
An
An
gr
A
wrw
dt
dФ
wke в
S
в
q
вых
в
22
2
0
0
1
1
5,7
,
где А 11l0-3
g0
2
G2
, сек2
– постоянная величина; go – электрическая
проводимость элемента ротора, ограниченного двугранным углом в 1
рад; G – магнитная проводимость по продольной и поперечной осям
машины; w, wB– число витков обмоток статора (выходной и воз-
буждения); h – обмоточный коэффициент выходной обмотки; rSв – ак-
тивное сопротивление обмотки возбуждения; UB – напряжение воз-
буждения.
В работе Ф. Феттера [104] ротор ДУ представлен в виде двух
эквивалентных замкнутых накоротко обмоток, оси которых совпа-
дают соответственно с продольной d и поперечной q осями машины
(т. е. с осями обмоток возбуждения и выходной). Ф. Феттером по-
лучено уравнение выходной ЭДС в дифференциальной форме, пока-
зывающее, что выходная ЭДС является не только функцией ускоре-
ния, но и функцией скорости (2
).
031 22
dt
de
r
L
dt
d
kIkMe вых
R
q
qdвqвqвых
,
где Lq – эквивалентная индуктивность роторной «обмотки» q; Мq –
взаимная индуктивность между выходной обмоткой и поперечной
«обмоткой» ротора; rR – активное сопротивление ротора; kqв kqd – ко-
эффициенты пропорциональности, определяющие составляющие тока
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-74-320.jpg)


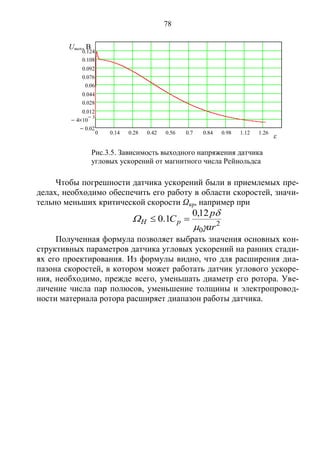
![79
ГЛАВА 4. НАГРУЗОЧНО-ИЗМЕРИТЕЛЬНЫЕ
УСТРОЙСТВА ДЛЯ ИСПЫТАНИЯ
ЭЛЕКТРОДВИГАТЕЛЕЙ МАЛОЙ МОЩНОСТИ
Для испытания электродвигателей малой мощности разрабо-
тано много различных нагрузочно-измерительных устройств [67,
70]. Значительная часть из них выполнена с полым немагнитным
ротором, который имеет минимально возможный момент инерции и
создает минимально возможный момент вентиляционных потерь.
Некоторые наиболее типичные конструкции таких устройств рас-
смотрены ниже.
4.1. Электромагнитный тормоз-моментомер
В серийном производстве любой измерительный прибор пове-
ряется службами главного метролога и в дальнейшем пломбируется.
По этой причине он должен иметь закрытую измерительную систе-
му. Применительно к электромагнитным тормозам это выполнить
достаточно трудно [66]. Один из возможных вариантов решения этой
проблемы представлен на рис. 4.1.
67
8
9
10
11
1
12
1
13
114
115
1
16
1
Рис.4.1. Тормоз-моментомер единой серии ТЕС
4
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-79-320.jpg)
![80
Тормоз-моментомер единой серии ТЕС [116] имеет измери-
тельный узел, поворачивающийся на шарикоподшипниках 15 или на
ножевых опорах. Измерительный узел состоит из рамки магнито-
провода 4 с гильзой 13, полюсных наконечников 10, груза-
противовеса 16 на тарировочном диске 14 и стрелки 12, расположен-
ной против шкалы 5. Рамка магнитопровод 4, гильза 13 и полюсные
наконечники 10 создают замкнутую систему, по которой замыкается
поток обмотки возбуждения 11. Эта система воспринимает вращаю-
щий момент стакана 8, закрепленного на валу испытываемого дви-
гателя и увлекается им в направлении своего вращения. Равный, но
противоположно направленный тормозной момент приложен к ста-
кану и к валу испытываемого двигателя.
Груз-противовес 16 и стрелка 12 как обычный маятниковый из-
мерительный механизм осуществляют измерение вращающего мо-
мента, приложенного к магнитопроводу.
Испытываемый двигатель устанавливается в самоцентрирую-
щиеся тиски 6, расположенные на основании 2, одна губка которых
несет призму, а другая – прижимную ленту. Для обеспечения соос-
ности прибора и испытываемого двигателя ходовой винт рисков пе-
ремещает губки на различные расстояния – губку с призмой на
большее расстояние, чем губку с ленточкой. При этом угол призмы
связан с шагами резьбы ходового винта следующим соотношением:
ïð
ë
2
sin
t
t
,
где φ– полный угол призмы; tл – шаг резьбы, перемещающей губку с
ленточкой; tпр – шаг резьбы, перемещающий губку с призмой.
Для фиксирования измерительного узла при транспортировке
прибор имеет арретир 5, а для успокоения стрелки – механический
демпфер. Установка стрелки прибора на нуль производится винта-
ми 1.
Прибор имеет кожух 7, предохраняющий измерительный меха-
низм от случайных повреждений и несанкционированного доступа.
Предусмотрена возможность пломбирования прибора после проверки
контролирующими службами.
На основе рассмотренной конструкции разработана серия тор-
мозов-моментомеров, позволяющая испытывать все типы микродви-
гателей постоянного и переменного тока, кроме тихоходных (шаго-
вых и редукторных). Серия охватывает диапазоны вращающих
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-80-320.jpg)
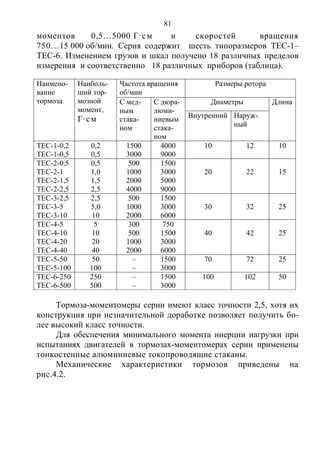
![82
Применение токопроводящих стаканов, имеющих меньшие диа-
метры, чем диски, позволило также уменьшить момент вентиляцион-
ных потерь дозначений, которые можно не учитывать, не выходя
при этом за пределы допустимых погрешностей прибора.
4.2. Электродинамический моментомер
Для измерения малых вращающих моментов с относительно не-
большой погрешностью может быть применен электродинамический
моментомер [11], общий вид, которого показан на рис. 4.3.
М
0,2
0,1
3000 6000
n
об/мин
мН·м
ТЕС-2
0
а)
М
4
2
3000 6000
n
об/мин
мН·м
ТЕС-3
0
б)
М
10
5
3000 6000
n
об/мин
мН·м
ТЕС-4
0
в)
М
500
250
3000 6000
n
об/мин
мН·м
ТЕС-6
0
г)
дюралюминиевый стакан, U = 24 В;
дюралюминиевый стакан, U = 12 В;
медный стакан, U = 24 В.
Рис. 4.2. Механические характеристики тормозов-
моментомеров серии ТЕС
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-82-320.jpg)




![87
ходимо непосредственное преобразование углового ускорения в
напряжение и не допустимо запаздывание сигнала. В качестве такого
датчика можно применять машину с полым немагнитным ротором или
специально изготовленный датчик.
В зарубежной литературе представлено много патентов специа-
лизированных датчиков ускорения с полыми, дисковыми и линейны-
ми роторами [122], которые называются датчиками Феррариса (Ferra-
ris sensor) по аналогии с известным диском Феррариса. Некоторые ти-
пы датчиков выпускаются серийно.Так, датчик угловых ускорений с
полыми немагнитными роторами АСС70 и АСС74 выпускаются
немецкой фирмой BAUMER. Эти датчики применяются в отечествен-
ных электроприводах
Исследованиями методов определения динамических моментов в
переходных режимах электрических машин занимались практически во
всех развитых капиталистических странах [105, 108, 109, 110]. Анализ
этих работ показывает, что методы определения динамических момен-
тов и угловых ускорений используются не только при исследователь-
ских испытаниях, но и при промышленных испытаниях для проверки ме-
ханических характеристик в поточном производстве, а также для полной
автоматизации процесса испытаний.
Одной из первых в нашей стране исследовала методы измерения
динамических моментов асинхронных двигателей Сомихина Г.С.
[160]. Для измерения угловых ускорений она использовала электриче-
скую машину с полым немагнитным ротором.
Исследованиями переходных режимов электродвигателей и раз-
работкой оборудования для измерения динамических моментов занима-
лись многие отечественные ученые. Наиболее полную конструктивную
проработку, вплоть до разработки приборов, выполнили Дубенский
А.А. и Варфоломеев Л.П. Разработанный Дубенским А.А. прибор
ПНМХ для непосредственного наблюдения механических характери-
стик двигателей имел в качестве датчика угловой скорости асинхрон-
ный тахогенератор с полым немагнитным ротором. Прибор также имел
встроенное регистрирующее устройство в виде электронно-лучевой
трубки, на вертикальные пластины которой подавалось выпрямленное
напряжение с тахогенератора (пропорциональное частоте вращения ис-
пытуемого двигателя), а на горизонтальные пластины – это же напря-
жение, но после дифференцирования и усиления (пропорциональное уг-
ловому ускорению испытуемого двигателя).
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-87-320.jpg)
![88
В усовершенствованном варианте прибора ПНМХ использован так-
же электромашинный датчик углового ускорения, выполненный на базе
машины полым ротором. Поперечный магнитный поток датчика, про-
порциональный угловой скорости ротора, непосредственно использу-
ется для получения сигнала вертикального отклонения луча регистри-
рующей электронно-лучевой трубки. Для этого выполнен специальный
магнитопровод, на котором расположена измерительная обмотка, фор-
мирующая напряжение, пропорциональное производной поперечного
магнитного потока по времени (и угловому ускорению испытуемого дви-
гателя). Это напряжение после усиления обеспечивает горизонтальное
отклонение луча.
Применение в качестве первичного преобразователя электриче-
ской машины с полым ротором обусловило основные недостатки прибо-
ра ПНМХ:
1) значительный тормозной момент, вносимый датчиком на вал дви-
гателя;
2) низкая точность определения механических характеристик;
3) отсутствие информации о временной координате.
4) нечувствительность к направлению вращения , что не позволя-
ет исследовать переходные режимы синхронных двигателей, у которых
возможно при включении изменение направление вращения.
Эти недостатки удалось устранить в приборах с частотным таходатчи-
ком [69].
Одним из таких приборов является характериограф ХМ-3, пред-
назначенный для регистрации динамических механических характери-
стик микродвигателей. Высокие динамические показатели характерио-
граф ХМ-3 имеет благодаря частотному фотоэлектрическому тахо-
датчику, в котором применен электрический способ дополнительной
модуляции потока излучения [119]. К достоинствам этого прибора сле-
дует отнести также малый момент инерции модулятора (не более 1·10-
7
кг·м2
), закрепляемого на валу испытуемого микродвигателя, что поз-
воляет исследовать динамические режимы микродвигателей с малым
моментом инерции ротора.
Структурная схема характериографа ХМ-3 приведена на рис. 4.6.
Она содержит задающий генератор G, формирователь трехфазной си-
стемы пульсирующих токов U1, таходатчик BV, предварительный
усилитель А1, преобразователь частоты в напряжение U2, фильтр
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-88-320.jpg)


![91
где ωо дв – скорость идеального холостого хода двигателя.
Масштаб времени, с/мм, определяется по записи отметчика вре-
мени:
mt=tx/x,
где х – длина осциллограммы, соответствующая выбранному отрез-
ку времени, например, tx =0,1 с.
Для осуществления динамической тарировки не требуется про-
ведения специальных опытов. Однако непременными условиями ее
применения являются линейность измерительной системы акселеро-
метра, постоянная скорость перемещения светочувствительной бума-
ги осциллографа и информация об изменении скорости ∆ω.
Таходатчик характериографа ХМ-3 использует в качестве излу-
чателей диоды инфракрасного диапазона АЛ108А. Тридцать диодов
образуют три группы, каждая из которых подключена к соответству-
ющей фазе формирователя пульсирующих токов. В качестве фотопри-
емника используется фотодиод типа ФД-К-155. Модулятор цилиндри-
ческой формы (диаметром 20 мм) содержит 40 делений и выполнен из
алюминиевого сплава.
Дифференциатор характериографа ХМ-3 состоит из неинверти-
рующего дифференцирующего усилителя (см. рис. 16) и однозвен-
ного активного фильтра, предназначенного для подавления высокоча-
стотных помех и обеспечения требуемой нагрузочной способности ак-
селерометра. Фильтр реализует частотные характеристики фильт- pa
Чебышева второго порядка с неравномерностью 0,5 дБ, частота среза
которого составляет 2,5 кГц. Увеличение нагрузочной спо-собности
достигается использованием комплементарного эмиттерно-го повто-
рителя.
Диапазон измерения угловых ускорений изменяется путем из-
менения постоянной времени дифференцирования, которая может;
быть установлена равной 2, 10 или 50 мс. Номинальное выходное
напряжение акселерометра также равно 10 В, максимальный ток,
нагрузки – 0,1 А.
Для упрощения выбора требуемой постоянной времени диф-
ференциатора при измерениях характериограф имеет пиковый детек-
тор напряжения акселерометра.
Оригинальную конструкцию имеет портативный характерио-
граф, защищенный патентом №2334236 [120]. Он выполнен на основе
современной элементной базы, содержит однокристальный микро-
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-91-320.jpg)



![95
СПИСОК ЛИТЕРАТУРЫ
1. Анненков, А.Н. Развитие научных основ моделирования и
анализа электромагнитных процессов для систем проектирования
асинхронных двигателей с токопроводящим слоем ротора: автореф.
Дис. …докт. техн. наук/ А.Н. Анненков. –Воронеж, 2005.
2. Анненков, А.Н. Аналитическая модель для исследования элек-
тромагнитных процессов в управляемых асинхронных микромашинах
с полым ротором/ А.Н.Анненков, Р.О. Нюхин// Машиностроитель. –
2006. – №12.
3. Анненков, А.Н. Моделирование электромагнитных процессов
в управляемых асинхронных машинах с полым ротором/ А.Н. Аннен-
ков, Р.О. Нюхин// Машиностроитель. – 2006. – №3.
4. Анненков, А.Н. Рациональное соотношение между размерами
в перфорированном полом роторе асинхронной микромашины/ А.Н.
Анненков, Р.О. Нюхин// Машиностроитель. – 2006. – №8.
5. Балашова, Н.А. Определение оптимальных соотношений при
проектировании серии управляемых двухфазных асинхронных двига-
телей с полым ротором/ Н.А. Балашова// Труды ЛИАП, – 1967. – Вып.
52.
6. Батоврин, А.А. К расчету параметров полых роторов/ А.А. Ба-
товрин// Вопросы радиоэлектроники. (Серия 12; вып. 4).
7. Бахвалов, Н.С. Численные методы в задачах и упражнениях/
Н.С. Бахвалов, А.В.Лапин, Е.В.Чижонков; под ред. В.А. Садовничего.
– М.: Высш. шк., 2000.
8. Бинс, К. Анализ и расчет электрических и магнитных полей:
[перевод]/ К.Бинс, П. Лауренсон. – М.: Энергия, 1979.
9. Брынский, Е.А. Электромагнитные поля в электрических маши-
нах/ Е.А. Брынский, Я.Б. Данилевич, В.И. Яковлев. – Л.: Энергия, Ле-
нинградское отделение, 1979.
10.Валдманис, Я.Я. Нахождение электромагнитного поля в беско-
нечной полосе в поле плоских бесконечных индукторов/ Я.Я. Валдма-
нис, Ю.Я. Михельсон // Изв. АН. Латв. ССР – 1965.– №1. – (Серия
«Физика и технические науки»).
11.Варфоломеев, Л.П. Прибор для снятия механических характери-
стик электродвигателей/ Л.П. Варфоломеев, И.Ш. Либин, А.Ш. Чер-
няк// Электротехника. – 1973. – №11.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-95-320.jpg)


![98
37.Кирюхин, В.П. Аналитическое определение интегральных па-
раметров тонкостенных немагнитных экранов индукционных электри-
ческих машин/ В.П. Кирюхин// Электричество. – 1970. – №5.
38.Кирюхин, В.П. Аналитическое определение интегральных па-
раметров тонкостенных немагнитных экранов электрических машин/
В.П. Кирюхин // Электричество. – 1973. – № 9.
39.Ковалев, Е.Б. Автоматизация измерений при испытаниях и ис-
следованиях асинхронных двигателей/ Е.Б. Ковалев. [и др]. – Элек-
трическая промышленность. Электрические машины. – 1984. – № 4.
40.Ковач, К. П. Переходные процессы в машинах переменного то-
ка/ К.П. Ковач, И. Рац.– М.: Госэнергоиздат, 1963.
41.Копылов, И.П. Математическое моделирование электрических
машин/ И. П. Копылов.– М.: Высш. шк., 2001.
42.Копылов, И.П. Математическое моделирование асинхронных
машин/ И.П. Копылов, Ф.А. Мамедов, В.А. Беспалов. – М.: Энергия,
1969.
43.Круминь, Ю.К. Взаимодействие бегущего магнитного поля с
проводящей средой/ Ю.К. Круминь. – Рига: Зинатне, 1969.
44.Кузнецов, Н.Е. Расчет электромагнитных муфт скольжения с
неферромагнитным якорем/ Н.Е. Кузнецов// Автоматика и телемеха-
ника. – 1964.
45.Лабудев, С.А. Динамические методы опытного определения ме-
ханических характеристик асинхронных двигателей/ С.А. Лабудев//
Изв высш. учеб. заведений СССР. Энергетика. – 1966. – № 8.
46.Лабудев, С.А. Динамические свойства асинхронного тахогене-
ратора в режиме акселерометра. / С.А. Лабудев// Параметры электри-
ческих машин переменного тока.– Киев: Наукова думка, 1968.
47.Лабудев, С.А. Осциллографирование электромагнитного момен-
та электрических машин при помощи интегрирующих схем с датчи-
ками ЭДС Холла/ С.А. Лабудев// Энергетика и электротехническая
промышленность. – Киев, 1964.– № 4.
48.Ладензон, З.А. К определению моментов асинхронного двигате-
ля в переходных режимах/З.А. Ладензон// Электромашиностроение и
электрооборудование. – 1965.– Вып. I.
49.Либин, И.Ш. Прибор для исследования высокоскоростных мик-
родвигателей/ И.Ш. Либин, Л.П. Варфоломеев// Приборы и техника
эксперимента.–1966. – № 5.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-98-320.jpg)



![102
88.Хайруллин, И.Х. Управляемая муфта-тормоз/ И.Х. Хайрулин,
Ф.Р. Исмагилов, Д.И. Богатырев [и др]// Машиностроитель. – 1986. –
№4.
89.Хайруллин, И.Х. Расчет оптимальных геометрических соотно-
шений конического ротора с учетом реакции поля вихревых токов/
И.Х. Хайрулин, Ф.Р. Исмагилов, М.Н. Нурмухаметов// Электротехни-
ка. – 1986. – №8.
90.Хайруллин, И.Х. Расчет электромагнитного момента демпфера с
немагнитным коническим ротором с учетом реакции магнитного поля
вихревых токов/ И.Х. Хайрулин, Ф.Р. Исмагилов, М.Н. Нурмухаме-
тов// Электромеханика. – 1986. – №8.
91.Хайруллин, И.Х. Электромагнитные демпферы с продольными
прорезями полого ротора/ И.Х. Хайрулин, Ф.Р. Исмагилов, Р.Р. Сата-
ров// Электротехника.– 2000. – №8.
92.Хайруллин, И.Х. К расчету электромагнитного момента демп-
фера с коническим ротором/ И.Х. Хайрулин, М.Н. Нурмухаметов, Ф.Р.
Исмагилов// Электричество. – 1979. – №11.
93.Хайруллин, И.Х. Влияние вторичной системы на электромаг-
нитный момент конического демпфера/ И.Х. Хайрулин, М.Н. Нурму-
хаметов, Ф.Р. Исмагилов// Электротехника. – 1980. – №6.
94.Хайруллин, И.Х. Оптимальные соотношения в электромагнит-
ном демпфере при работе в системе управления/ И.Х. Хайрулин, Ф.Р.
Исмагилов// Электротехника. – 1981. – №11.
95.Хайруллин, И.Х. Электромагнитный момент малоинерционного
тормоза с полым немагнитным ротором сложной конфигурации/ И.Х.
Хайруллин// Электричество. – 1977. – № 4.
96.Хайруллин, И.Х. Электромагнитные переходные процессы в не-
явнополюсном магнитоэлектрическом тормозе с полым ротором/ И.Х.
Хайруллин// Электричество. – 1978. – № 10.
97.Чечет, Ю.С. Электрические микромашины автоматических
устройств/ Ю.С. Чечет. – М.: Госэнергоиздат, 1964.
98.Шаров, В.С. Электромагнитные муфты скольжения/ В.С. Ша-
ров. – М.: Госэнергоиздат, 1958.
99.Шипилло, В.П. Эквивалентность режимов динамического тор-
можения и пуска асинхронной машины/ В. П. Шипилло// Электриче-
ство. – 1958. – №10.
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»](https://image.slidesharecdn.com/706-150523210923-lva1-app6892/85/706-102-320.jpg)